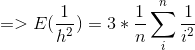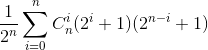2020 Multi-University Training Contest 5 (1001 几何数学公式推导、1007 换根dp 1009 数学公式推导、1012 组合数学公式推导)
比赛链接
最近比较喜欢数学题,特来补补这两题
1001-Tetrahedron
题意:给你一个正方体一角的图形,已知 a、b、c, 求1/h^2 的期望
做法:利用勾股定理,求出AB AC BC 的值,再用海伦公式求出ABC的面积,利用体积相等原则,求出h的高度。
海伦公式:
求ABC面积 就有点复杂了。参考博客:博客
可以得到
预处理前缀平方和即可
#pragma GCC optimize(2)
#include
#include
#include
#include
#include
#include
#include 1007-Tree
题意:给你一颗树,选择某些节点,且节点度数大于k的只有一个,其余节点 度数均小于等于k。
做法:换根dp,设dp[u]为选择子树u 且 度数小于等于k-1 时的最大值。那么 每次定义root为根节点的时候 就将根节点所有权值加起来,而不是dp[u]了,随便换根下 就可以了。
换根细节部分有点难写。因为我每次换根的 从 u 换到v 的时候,需要判断下,v是否之前已经加入u 的dp值内,加了的话需要去掉,再加一个 其他节点的dp值 维持k-1个节点。这里我们可以先提前加好k个值。
如果v 是前k-1个,就减去,如果不是 就减去第k个即可。很妙的换根dp
#include
#define rep(i,a,b) for(int i=a;i<=b;++i)
using namespace std;
const int N=2e5+10;
typedef long long ll;
vector >G[N], g[N];
int n, k;
ll dp[N], ans, sum[N];
ll read()
{
ll x=0,w=1;char c=getchar();
while(c<'0'||c>'9') {if(c=='-')w=-1;c=getchar();}
while('0'<=c&&c<='9') {x=x*10+c-'0';c=getchar();}
return x;
}
bool cmp(pair a,pair b)
{
return a.first>b.first;
}
void dfs(int u, int fa)
{
for(auto it:G[u]){
if(it.second == fa) continue;
dfs(it.second, u);
sum[it.second] = dp[it.second] + it.first;
//printf("u:%d v:%d sum:%lld\n", u, it.second, sum[it.second]);
g[u].push_back({sum[it.second], it.second});
}
sort(g[u].begin(), g[u].end(), cmp );
int len = min(k-1, int(g[u].size()));
for(int i = 0; i < len; ++i){
dp[u] += g[u][i].first;
}
//printf("u:%d len:%d dp:%lld\n", u, len, dp[u]);
}
void dfs1(int u, int fa, ll w)
{
if(fa != 0) g[u].push_back({w,fa});
sort(g[u].begin(), g[u].end(), cmp);
int len = min(k, (int)g[u].size());
ll res = 0;
for(int i = 0; i < g[u].size(); ++i){
//printf("u:%d f:%lld w:%lld\n", u, g[u][i].first, w);
res += g[u][i].first;
}
//printf("u:%d res:%lld sz:%d\n", u, res, g[u].size());
ans = max(ans, res);
res = 0;
for(int i = 0; i < len; ++i){
res += g[u][i].first;
}
for(int i = 0; i < g[u].size(); ++i){
int v =g[u][i].second;
if(v == fa) continue;
ll tmp;
if(i < len){
tmp = res - sum[v] + sum[v] - dp[v];
}
else{
//printf("sz:%d len:%d i:%d\n",g[u].size(), len, i);
tmp = res - g[u][k-1].first + sum[v] - dp[v];
}
dfs1(v, u, tmp);
}
}
int main()
{
int _=read();while(_--)
{
n = read(), k = read();
rep(i, 1, n) G[i].clear(), g[i].clear(), sum[i] = dp[i] = 0;
rep(i, 2, n)
{
int u = read(), v = read();
ll w = read();
G[u].push_back({w,v});
G[v].push_back({w,u});
}
if(k==0){
puts("0");continue;
}
rep(i, 1, n) sort(G[i].begin(), G[i].end());
ans = 0;
dfs(1,1);
//rep(i, 1, n) printf("i:%d dp:%lld\n", i, dp[i]);
dfs1(1, 0, 0);
printf("%lld\n", ans);
}
}
/*
1
5 0
1 2 5
2 3 2
2 4 3
2 5 4
*/
1009-Paperfolding
题意:折纸游戏,给你一张纸,每次可以选择横着对折一次,或者竖着对折一次,给你n,要求折n次,求最后 在中间切个十字架时被分成多少块的期望
做法:这题有点考验几何想象能力。无论横着折 竖着折无论顺序不会影响最后每次折对该行(列)的贡献,于是共有 2^n次折法,推导出一个很奇妙的结论,当某个方向对折x次 又切十字架型,那么对这行能产生的块是2^x+1个,列类似 2^y+1,那么两个相乘就是总块数。
那么答案就是
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb emplace_back
#define pii pair
#define mk make_pair
using namespace std;
typedef long long ll;
const ll mod = 998244353;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
ll powmod(ll a,ll b) {ll res=1;a%=mod;
assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
inline ll read()
{
ll x=0,w=1; char c=getchar();
while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();}
while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();}
return w==1?x:-x;
}
int main()
{
int _ = read();while(_--)
{
ll n = read();
ll ans = powmod(2, n);
ll res = 2*powmod(3,n)*powmod(powmod(2,n),mod-2)%mod;
ans = (ans + 1 + res ) %mod;
printf("%lld\n",ans);
}
} 1012-Set1
题意:给你1到n的排列,每次选择一个最小的数删除,接着随机删除一个数。求 最后只剩下 i 时 的概率是多少?n保证奇数
做法:自闭了,看题解:
做法:类似 配对,因为每次都是操作1加操作2的形式。
我们来分析下图红圈怎么来的吧
假设有这么一题:n个数,两两配对,求方案数。
第一次选一个,选完第一个剩余的再选一个 两个的顺序可以交换:
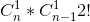
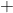
......
代码就懒的打了