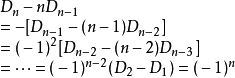HDU1465 不容易系列之一（错排问题）

                                          不容易系列之一

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 28892    Accepted Submission(s): 12643

 

Problem Description

大家常常感慨，要做好一件事情真的不容易，确实，失败比成功容易多了！
做好“一件”事情尚且不易，若想永远成功而总从不失败，那更是难上加难了，就像花钱总是比挣钱容易的道理一样。
话虽这样说，我还是要告诉大家，要想失败到一定程度也是不容易的。比如，我高中的时候，就有一个神奇的女生，在英语考试的时候，竟然把40个单项选择题全部做错了！大家都学过概率论，应该知道出现这种情况的概率，所以至今我都觉得这是一件神奇的事情。如果套用一句经典的评语，我们可以这样总结：一个人做错一道选择题并不难，难的是全部做错，一个不对。

不幸的是，这种小概率事件又发生了，而且就在我们身边：
事情是这样的——HDU有个网名叫做8006的男性同学，结交网友无数，最近该同学玩起了浪漫，同时给n个网友每人写了一封信，这都没什么，要命的是，他竟然把所有的信都装错了信封！注意了，是全部装错哟！

现在的问题是：请大家帮可怜的8006同学计算一下，一共有多少种可能的错误方式呢？

 

Input

输入数据包含多个多个测试实例，每个测试实例占用一行，每行包含一个正整数n（1

 

Output

对于每行输入请输出可能的错误方式的数量，每个实例的输出占用一行。

 

Sample Input

2 3

 

Sample Output

1 2

这道题要自己模拟很麻烦，如果找到规律后就很快了。

规律见代码：

#include 
using namespace std;
#define fr(i, r, n) for(int i = r; i < n; ++i)
const int maxn = (int)2e5 +10;
typedef long long ll;

int main()
{
    int n;
    ll arr[30];
    memset(arr, 0, sizeof arr);
    fr(i, 1, 25)//规律
    {
        if(i&1)
            arr[i+1] = arr[i]*(i+1)+1;//当i为奇数时，下一个的数值等于这一个的数值*下一个的序号+1
        else
            arr[i+1] = arr[i]*(i+1)-1;//偶数时，下一个的数值等于这一个的数值*下一个的序号-1
    }
    while(cin>>n)
    {
        cout<

但是如何找到规律呢，我们可以对前几个数进行打表，如下：

    int arr[20];
    int ans;
    for(int i = 1; i <=10; i++)
    {
        ans = 0;
        for(int j = 1; j <= i; j++) arr[j] = j;
        do{
            for(int k = 1; k <= i; k++)
            {
                if(arr[k] == k)
                    break;
                if(k == i) ans++;
            }
        }while(next_permutation(arr+1, arr+i+1));
        cout<

这里的next_permutation是一个全排列的函数，作用是更改排列为字典序的下一个排列。如果没有下一个排列，就返回0，也就是while的跳出条件。还有一个相似的函数是prev_permutation，更改排列为字典序的上一个排列。

 

727补充：这其实是一道非常经典的错排问题。

基本信息：

      错排问题是组合数学发展史上的一个重要问题，错排数也是一项重要的数。令  是  的一个错排，如果每个元素都不在其对应下标的位置上，即  ，那么这种排列称为错位排列，或错排、重排（Derangement）。我们从分析1 2 3 4的错排开始：

1 2 3 4的错排有:

4 3 2 1，4 1 2 3，4 3 1 2，

3 4 1 2，3 4 2 1，2 4 1 3，

2 1 4 3，3 1 4 2，2 3 4 1。

第一列是4分别与123互换位置，其余两个元素错排。

1 2 3 4->4 3 2 1，

1 2 3 4->3 4 1 2，

1 2 3 4->2 1 4 3。

第2列是4分别与312（123的一个错排）的每一个数互换

3 1 2 4->4 1 2 3，

3 1 2 4->3 4 2 1，

3 1 2 4->3 1 4 2。

第三列则是由另一个错排231和4换位而得到

2 3 1 4->4 3 1 2，

2 3 1 4->2 4 1 3，

2 3 1 4->2 3 4 1

上面的分析结果，实际上是给出一种产生错排的结果。

递归关系：

为求其递推关系，分两步走：

第一步，考虑第n个元素，把它放在某一个位置，比如位置k，一共有n-1种放法；

第二步，考虑第k个元素，这时有两种情况：（1）把它放到位置n，那么对于除n以外的n-1个元素，由于第k个元素放到了位置n，所以剩下n-2个元素的错排即可，有  种放法；（2）第k个元素不放到位置n，这时对于这n-1个元素的错排，有 

种放法。

根据乘法和加法法则，综上得到 

特殊地，  。此外，存在

因此，  。

.............................................................................................................................来自百度百科