PyTorch入门实战教程笔记（十七）：过拟合1

PyTorch入门实战教程笔记（十七）：过拟合1

过拟合&欠拟合

在模型评估与调整的过程中，往往会遇到“过拟合”或“欠拟合”的情况。如何有效地识别“过拟合”和“欠拟合”现象，并有针对性进行模型调整，是不断改进机器学习模型的关键。那么过拟合和欠拟合具体是指什么现象呢？

过拟合(overfitting)是指模型的参数量，模型的表达能力，已经超越本身模型的复杂度。反应在评估指标上，就是模型在训练集上的表现很好，但在测试集和新数据上表现的较差。

欠拟合(underfitting)指的是模型在训练和预测时表现都不好的情况，一般少见。

下图形象的描述了过拟合和欠拟合的区别：

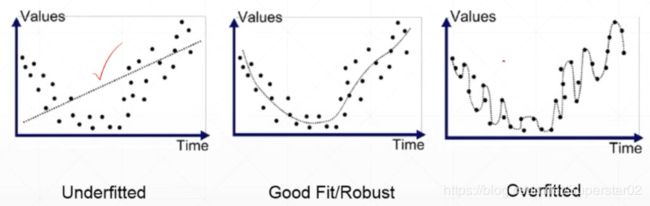
可以看出，图（1）是欠拟合的情况，图（3）则是过拟合的情况，模型过于复杂，把噪声数据的特征也学习到模型中，导致模型的泛化能力下降，在后期应用过程中很容易输出错误的预测结果。
　　那么如果防止或者降低overfitting，我们有一下方法：

1）使用更多的训练数据。更多的样本能够让模型学习到更多更有效的特征，减小噪声的影响。当然，直接增加实验数据一般是很困难的，但是可以通过一定的规则来扩充训练数据。比如，在图像分类的问题上，可以通过图像的平移、旋转、缩放等方式扩充数据；更进一步地，可以使用生成式对抗网络来合成大量的新训练数据。

2）降低模型复杂度。在数据较少时，模型过于复杂是产生过拟合的主要因素，适当降低模型复杂度可以避免模型拟合过多的采样噪声。例如，在神经网络模型中 Dropout 减少网络层数、神经元个数等。

3）正则化（regularization）方法。给模型的参数加上一定的正则约束，比如将权值的大小加入到损失函数中。文章会详细讲解正则化方法。

4）集成学习方法。集成学习是把多个模型集成在一起，来降低单一模型的过拟合风险，如Bagging方法。

 

如何 降低“欠拟合” 风险的方法：

1）添加新特征。当特征不足或者现有特征与样本标签的相关性不强时，模型容易出现欠拟合。通过挖掘“上下文特征”“ID类特征”“组合特征”等新的特征，往往能够取得更好的效果。在深度学习潮流中，有很多模型可以帮助完成特征工程，如因子分解机、梯度提升决策树、Deep-crossing等都可以成为丰富特征的方法。

2）增加模型复杂度。简单模型的学习能力较差，通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如，在线性模型中添加高次项，在神经网络模型中增加网络层数或神经元个数等。

3）减小正则化系数。正则化是用来防止过拟合的，但当模型出现欠拟合现象时，则需要有针对性地减小正则化系数。

交叉验证

前面介绍了欠拟合和过拟合的相关概念及如何解决两者的方法，其中最常见的是过拟合，我们如何检测是否过拟合呢，如下图，我们想要的是蓝色线，但是由于网络出现过拟合，造成了黄色线的结果，虽然很好的拟合了原始数据黑色点，但是对于测试点橙色是不好，即训练的loss很低，但是测试的loss很高。

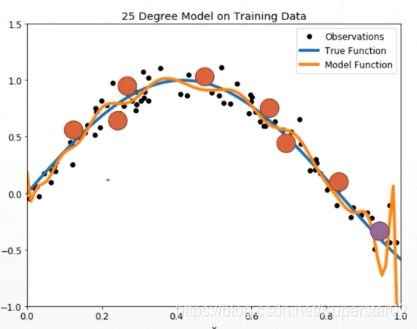
　　那么我们可以利用这种现象，我们把dataset划分为train set和test set, 数据集是同一数据，所以分布肯定是一样的，如果在train set表现好，test set表现差，那就是出现过拟合啦。在训练中，我们可以训练一个epoch，然后测试一次，然后看测试的performance，保留测试最好的网络参数，即网络训练的最好的模型。
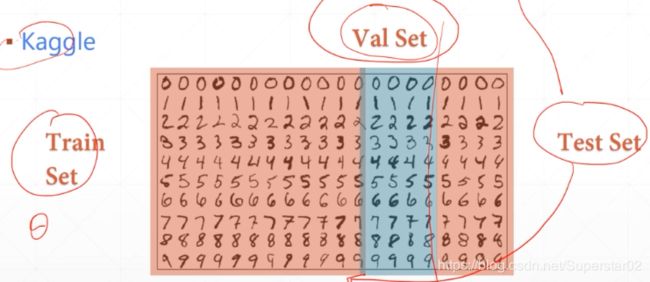
　　上面只是思路，一般我们做训练时，上述的test为validation（验证集），用来真真正正挑选参数的，而test是让客户来验证这个网络模型对的性能的。

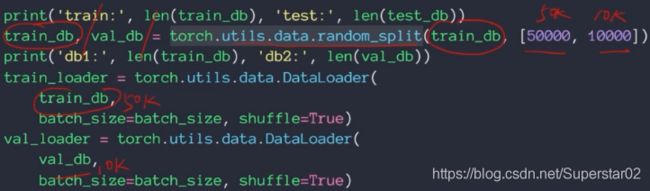
　　代码划分三个数据集实现，从MINIST下载的数据为train和test，所以我们使用torch.utils.data.random_split, 将train人为切割成50000,10000，来构建validation（验证集）。然后还有原来的10000 个test，

　　如果按照上述划分，有20k的数据没有来做backward，test的数据肯定是不能用的，但是val（验证集）是可以合理利用的，比如假设60000个数据有顺序，第一次把前50k，做train，后10k做验证集，第二次把前40k和后10k做train，40k-50k数据做验证集。。。以此类推，从时间上讲，这60k数据每一个都用于了backwrad，是有利于我们训练模型的，提升不太大，不过会稍微有提升。
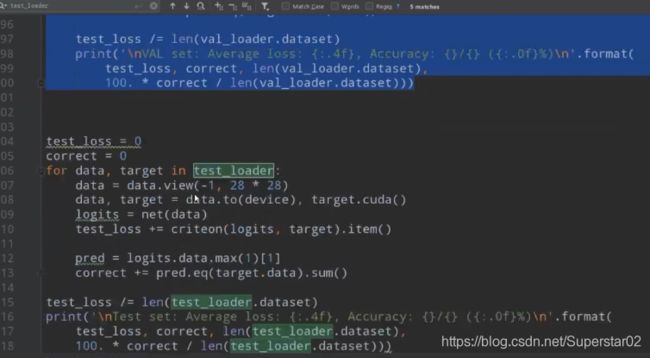
　　在代码实战中，我们在每一个epoch中用val_loader来做验证网络的参数，比如做了5000个epoch，在3612个epoch的验证集效果好，那么我们可以加载此模型的参数，然后用test集来训练。即在下图101-103行 加响应的代码来加载最好的模型参数，再用于测试。

正则化regularization

给模型的参数加上一定的正则约束，比如将权值的大小加入到损失函数中。之前的交叉熵loss大家应该还记得，我们在后面加一项，如下图：

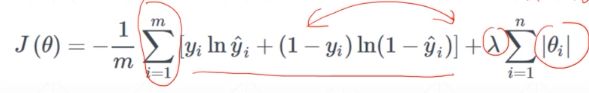
上式中λ有点类似于学习率，0.01这样子。这样子有什么好处呢，我们的loss的目标就是minimize，minimize前一部分，使得预测值和真实值的部分更加接近，minimize后一部分，使得θ参数的范数会接近0，也就是迫使参数的范数w/b的值接近于零，以减少模型的复杂度。怎么理解呢？解释1，看一维情况，如果参数接近于零，那么曲线是不是会更加平滑，泛化力也强，解释2，我们希望参数小，但是模型的表达能力还要足够用，那么就会β₀，β₁，β₂…的值，刚好能够很好的表达数据的分布，然后后面高维的参数就会非常小，会是网络结构退化成相当于更少次方的网络结构，使得网络即很好表达了数据分布，又降低了网络的复杂度，避免了overfitting。此外，这个除了叫Regularization外，还叫做weight decay。

更直观的角度来看，下图左图的表达能力比较强，分割面比较复杂，能够很好地学到复杂的模型，但是我们本身的数据时不复杂的，他学到的可能是一些噪声造成的，它的泛化能力就不强了。下图右图是我们加了L2-regularization的效果，分割面比较 平滑，具有较强的泛化能力，恰好是我们想要的。即正则化防止了过拟合。

两种常见的regularization如下图，L2-regularization是我们最常用的。

在pytorch中作L2-regularization非常方便，只需要设置weight _decay参数即可，也就数我们前面讲的λ参数，需要注意的是设置这个参数之后，会使网络的参数降低很多，如果没有过拟合，设置weight _decay，会使性能下降，因为当前没有过拟合，说明网络当前的复杂度刚好，设置会使复杂度降低，导致性能下降。如果过拟合，设置weight _decay，网络的性能基本不受影响，并且test性能会提高一点，也就是泛化能力会增强。

对于L1正则化，pytorch目前没有提供相应的接口，我们可以通过以下代码实现：