9. 二叉堆

1 堆

1. 设计一种数据结构，用来存放整数，要求提供 3 个接口
   1. 添加元素
   2. 获取最大值
   3. 删除最大值
      
2. 堆中获取最大值：O(1)、删除最大值：O(logn)、添加元素：O(logn)
3. 堆的性质
   1. 是一种树状的数据结构（不要跟内存模型中的“堆空间”混淆）
   2. 任意节点的值总是 ≥（ ≤ ）子节点的值
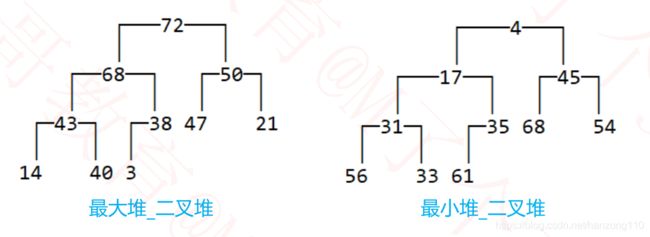
   3. 如果任意节点的值总是 ≥ 子节点的值，称为：最大堆、大根堆、大顶堆
   4. 如果任意节点的值总是 ≤ 子节点的值，称为：最小堆、小根堆、小顶堆
   5. 堆中的元素必须具备可比较性
      

2 二叉堆（Binary Heap）

1. 二叉堆的逻辑结构就是一棵完全二叉树，所以也叫完全二叉堆
2. 鉴于完全二叉树的一些特性，二叉堆的底层（物理结构）一般用数组实现即可
   
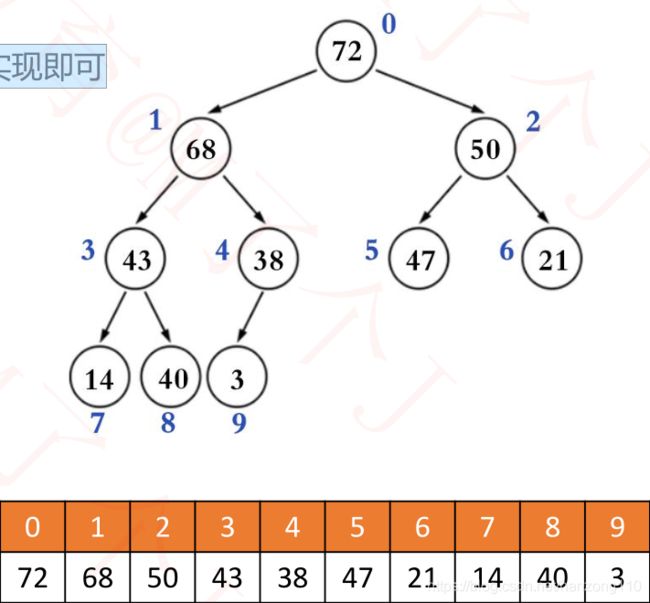
3. 获取最大值：直接获取数组索引0的元素
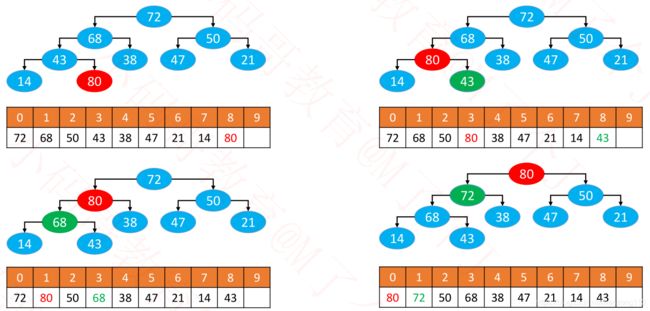
4. 添加
   1. 将元素添加到数组最后一个位置
   2. 对该元素进行上滤(sift up)
      1. 循环执行如果node>父节点，与父节点换位
      2. 如果node<=父节点，退出循环
         
      3. 上滤的优化：不交换位置，只让父节点依次覆盖上溢的节点，最后停留的位置由上溢节点覆盖
         
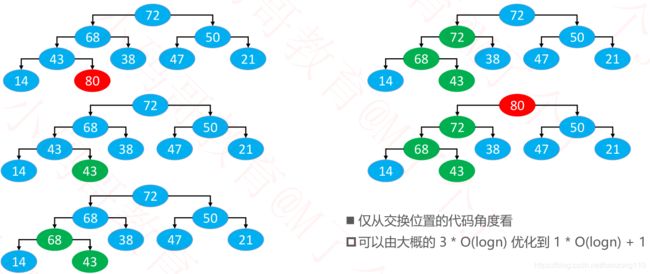
      4. 上滤时间复杂度为O(logn)
5. 删除
   1. 使用数组中最后一个元素覆盖第一个元素，删除最后一个元素
   2. 将新的第一个元素进行下滤
      1. 循环，如果 node < 最大的子节点，与最大的子节点交换位置
      2. 如果 node ≥ 最大的子节点， 或者 node 没有子节点，退出循环
   3. 下滤时间复杂度也是O(logn)
      
6. replace：使用新元素替换堆顶元素
   1. 使用新传入的元素替换数组中第一个元素
   2. 对新的第一个元素进行下滤
7. 批量建堆
   1. 自上而下的上滤：从非根节点开始，从上到下，从左到右，对所有节点进行上滤，逻辑其实与添加逻辑相同，因此可以保证结果有堆的性质
      
   2. 自下而上的下滤：从第一个非叶子节点开始，从右至左，从下到上，对所有节点进行下滤，和删除的逻辑类似，因此也能保证最后结果有堆的性质
      
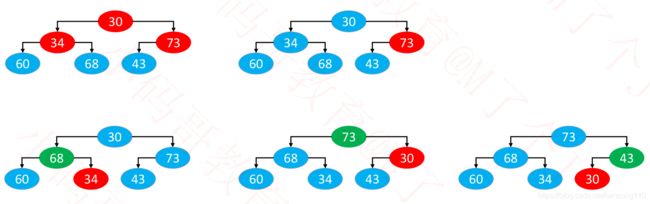
8. 批量建堆效率对比
   1. 对于自上而下的上滤，底层大量的节点，需要执行的上滤次数反而多，而对于自下而上的下滤，对于底层大量的节点，需要执行下滤的次数少
   2. 对于自上而下：时间复杂度就是所有节点的深度之和，复杂度为O(nlogn)
      1. 仅仅是叶子节点，就有近 n/2 个，而且每一个叶子节点的深度都是 O(logn) 级别的
      2. 因此，在叶子节点这一块，就达到了 O(nlogn) 级别
      3. O(nlogn) 的时间复杂度足以利用排序算法对所有节点进行全排序
   3. 对于自下而上：时间复杂度为所有节点的高度之和，复杂度为O(n)
   4. 因此批量建堆时，不要直接调用堆的add方法
9. 构建小顶堆：只需修改Comparator中compare逻辑，或者Comparable中compareTo逻辑
10. Heap

package com.mj.heap;

public interface Heap<E> {
	int size();	// 元素的数量
	boolean isEmpty();	// 是否为空
	void clear();	// 清空
	void add(E element);	 // 添加元素
	E get();	// 获得堆顶元素
	E remove(); // 删除堆顶元素
	E replace(E element); // 删除堆顶元素的同时插入一个新元素
}

11. AbstractHeap

package com.mj.heap;

import java.util.Comparator;

@SuppressWarnings("unchecked")
public abstract class AbstractHeap<E> implements Heap<E> {
	protected int size;
	protected Comparator<E> comparator;
	
	public AbstractHeap(Comparator<E> comparator) {
		this.comparator = comparator;
	}
	
	public AbstractHeap() {
		this(null);
	}
	
	@Override
	public int size() {
		return size;
	}

	@Override
	public boolean isEmpty() {
		return size == 0;
	}
	
	protected int compare(E e1, E e2) {
		return comparator != null ? comparator.compare(e1, e2) 
				: ((Comparable<E>)e1).compareTo(e2);
	}
}

12. BinaryHeap

package com.mj.heap;

import java.util.Comparator;

import com.mj.printer.BinaryTreeInfo;

/**
 * 二叉堆（最大堆）
 * @author MJ Lee
 *
 * @param 
 */
@SuppressWarnings("unchecked")
public class BinaryHeap<E> extends AbstractHeap<E> implements BinaryTreeInfo {
	private E[] elements;
	private static final int DEFAULT_CAPACITY = 10;
	
	public BinaryHeap(E[] elements, Comparator<E> comparator)  {
		super(comparator);
		
		if (elements == null || elements.length == 0) {
			this.elements = (E[]) new Object[DEFAULT_CAPACITY];
		} else {
			size = elements.length;
			int capacity = Math.max(elements.length, DEFAULT_CAPACITY);
			this.elements = (E[]) new Object[capacity];
			for (int i = 0; i < elements.length; i++) {
				//不能直接使用传入的数组，不然外面对该数组改动，内部也会被改动，因此先将传入的数组拷贝一份
				this.elements[i] = elements[i];
			}
			heapify();
		}
	}
	
	public BinaryHeap(E[] elements)  {
		this(elements, null);
	}
	
	public BinaryHeap(Comparator<E> comparator) {
		this(null, comparator);
	}
	
	public BinaryHeap() {
		this(null, null);
	}

	@Override
	public void clear() {
		for (int i = 0; i < size; i++) {
			elements[i] = null;
		}
		size = 0;
	}

	@Override
	public void add(E element) {
		//由于二叉堆要求元素必须具备可比较性，所以不能传null值进来
		elementNotNullCheck(element);
		//就是复用之前动态数组的扩容逻辑
		ensureCapacity(size + 1);
		elements[size++] = element;
		siftUp(size - 1);
	}

	@Override
	public E get() {
		emptyCheck();
		return elements[0];
	}

	@Override
	public E remove() {
		emptyCheck();
		
		int lastIndex = --size;
		E root = elements[0];
		elements[0] = elements[lastIndex];
		elements[lastIndex] = null;
		
		siftDown(0);
		return root;
	}

	@Override
	public E replace(E element) {
		elementNotNullCheck(element);
		
		E root = null;
		//如果放入的是第一个元素，那么不需要删除，直接添加就可以了
		if (size == 0) {
			elements[0] = element;
			size++;
		} else {
			root = elements[0];
			elements[0] = element;
			siftDown(0);
		}
		return root;
	}
	
	/**
	 * 批量建堆
	 */
	private void heapify() {
		// 自上而下的上滤
//		for (int i = 1; i < size; i++) {
//			siftUp(i);
//		}
		
		// 自下而上的下滤
		for (int i = (size >> 1) - 1; i >= 0; i--) {
			siftDown(i);
		}
	}
	
	/**
	 * 让index位置的元素下滤
	 * @param index
	 */
	private void siftDown(int index) {
		E element = elements[index];
		int half = size >> 1;
		// 第一个叶子节点的索引 == 非叶子节点的数量
		// index < 第一个叶子节点的索引
		//对于完全二叉树，其非叶子节点，数量应该是floor(n/2)
		// 必须保证index位置是非叶子节点
		while (index < half) { 
			// index的节点有2种情况
			// 1.只有左子节点
			// 2.同时有左右子节点
			
			// 默认为左子节点跟它进行比较
			//编号从0开始，那么左子节点编号就是2i+1
			int childIndex = (index << 1) + 1;
			E child = elements[childIndex];
			
			// 右子节点，2i+2，其实就是左子节点+1
			int rightIndex = childIndex + 1;
			
			// 选出左右子节点最大的那个
			//如果索引在正常范围内，表示右子节点存在
			//如果右边比左边大，选右边元素作为child(右侧元素值赋给child，并将右侧元素索引给child)与element进行比较
			if (rightIndex < size && compare(elements[rightIndex], child) > 0) {
				child = elements[childIndex = rightIndex];
			}
			
			if (compare(element, child) >= 0) break;

			// 将子节点存放到index位置
			elements[index] = child;
			// 重新设置index
			index = childIndex;
		}
		elements[index] = element;
	}
	
	/**
	 * 让index位置的元素上滤
	 * @param index
	 */
	private void siftUp(int index) {
//		E e = elements[index];
//		while (index > 0) {
//			int pindex = (index - 1) >> 1;
//			E p = elements[pindex];
			//如果自身小于父节点，就不用继续上滤了
//			if (compare(e, p) <= 0) return;
//			
//			// 交换父子节点在数组中位置
//			E tmp = elements[index];
//			elements[index] = elements[pindex];
//			elements[pindex] = tmp;
//			
//			// 当做完一次交换之后，由新节点已经到了原来父节点的索引处，所以此时为了继续上滤，应该使用该节点当前的索引，继续上滤
//			index = pindex;
//		}
		E element = elements[index];
		//index>0才表示该节点有父节点，可以进行上滤
		while (index > 0) {
			//获取父节点索引
			int parentIndex = (index - 1) >> 1;
			E parent = elements[parentIndex];
			if (compare(element, parent) <= 0) break;
			
			//此处照比之前省略了两行代码，省略了每次将新添加的元素放入到新的位置的代码
			// 将父元素存储在index位置
			elements[index] = parent;
			
			// 重新赋值index
			index = parentIndex;
		}
		//当循环退出时，记录的index的位置，就是该节点最终应该放的位置
		elements[index] = element;
	}
	
	private void ensureCapacity(int capacity) {
		int oldCapacity = elements.length;
		if (oldCapacity >= capacity) return;
		
		// 新容量为旧容量的1.5倍
		int newCapacity = oldCapacity + (oldCapacity >> 1);
		E[] newElements = (E[]) new Object[newCapacity];
		for (int i = 0; i < size; i++) {
			newElements[i] = elements[i];
		}
		elements = newElements;
	}
	
	private void emptyCheck() {
		if (size == 0) {
			throw new IndexOutOfBoundsException("Heap is empty");
		}
	}
	
	private void elementNotNullCheck(E element) {
		if (element == null) {
			throw new IllegalArgumentException("element must not be null");
		}
	}

	@Override
	public Object root() {
		return 0;
	}

	@Override
	public Object left(Object node) {
		int index = ((int)node << 1) + 1;
		return index >= size ? null : index;
	}

	@Override
	public Object right(Object node) {
		int index = ((int)node << 1) + 2;
		return index >= size ? null : index;
	}

	@Override
	public Object string(Object node) {
		return elements[(int)node];
	}
}

3 Top K问题

1. 从 n 个整数中，找出最大的前 k 个数（ k 远远小于 n ）
2. 如果使用排序算法进行全排序，需要 O(nlogn) 的时间复杂度
3. 如果使用二叉堆来解决，可以使用 O(nlogk) 的时间复杂度来解决
4. 解决方案
   1. 新建一个小顶堆
   2. 扫描 n 个整数
   3. 先将遍历到的前 k 个数放入堆中
   4. 从第 k + 1 个数开始，如果大于堆顶元素，就使用 replace 操作（删除堆顶元素，将第 k + 1 个数添加到堆中）
   5. 扫描完毕后，堆中剩下的就是最大的前 k 个数

package com.mj;

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;

import com.mj.heap.BinaryHeap;
import com.mj.printer.BinaryTrees;

public class Main {
	static void test4() {
		// 新建一个小顶堆
		BinaryHeap<Integer> heap = new BinaryHeap<>(new Comparator<Integer>() {
			public int compare(Integer o1, Integer o2) {
				return o2 - o1;
			}
		});

		// 找出最大的前k个数
		int k = 3;
		Integer[] data = { 51, 30, 39, 92, 74, 25, 16, 93, 91, 19, 54, 47, 73, 62, 76, 63, 35, 18, 90, 6, 65, 49, 3, 26,
				61, 21, 48 };
		for (int i = 0; i < data.length; i++) {
			if (heap.size() < k) { // 前k个数添加到小顶堆
				heap.add(data[i]); // logk
			} else if (data[i] > heap.get()) { // 如果是第k + 1个数，并且大于堆顶元素
				heap.replace(data[i]); // logk
			}
		}
		// O(nlogk)
		BinaryTrees.println(heap);
	}
	public static void main(String[] args) {
		test4();
		test5();
	}
}

4 优先级队列（Priority Queue）

1. 按添加元素的从小到大顺序出队
2. 底层使用堆来实现，PriorityQueue就是Java中的最小堆

public int compareTo(Person o){
	//只要是使用自身的属性，减去传入的属性，就说明，遵守PriorityQueue的默认比较顺序(从小到大)
	//如果为o.boneBreak - boneBreak，说明与PriorityQueue的默认比较顺序完全相反，因此是从大到小，即最大堆
	return boneBreak - o.boneBreak;
}
public int compare(Integer o1, Integer o2) {
	//同理，如果为o1-o2，表示采用默认的比较顺序
	//如果为o2-o1，表示采用与默认相反的比较顺序
	return o2 - o1;
}