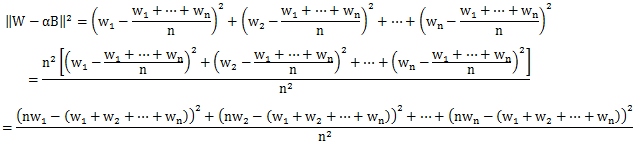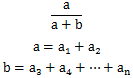2016 Multi-University Training Contest 2题解报告
此文章可以使用目录功能哟↑(点击上方[+])
多校做得越来越没底气了,难的不会,易的不对,前途坎坷...
话说多校都放题解了,不过还是打算自己写写,加深印象
2016 Multi-University Training Contest 2官方题解
链接→2016 Multi-University Training Contest 2
Problem 1001 Acperience
Accept: 0 Submit: 0
Time Limit: 4000/2000 MS (Java/Others) Memory Limit : 65536/65536K (Java/Others)
Problem Description
Deep neural networks (DNN) have shown significant improvements in several application domains including computer vision and speech recognition. In computer vision, a particular type of DNN, known as Convolutional Neural Networks (CNN), have demonstrated state-of-the-art results in object recognition and detection.
Convolutional neural networks show reliable results on object recognition and detection that are useful in real world applications. Concurrent to the recent progress in recognition, interesting advancements have been happening in virtual reality (VR by Oculus), augmented reality (AR by HoloLens), and smart wearable devices. Putting these two pieces together, we argue that it is the right time to equip smart portable devices with the power of state-of-the-art recognition systems. However, CNN-based recognition systems need large amounts of memory and computational power. While they perform well on expensive, GPU-based machines, they are often unsuitable for smaller devices like cell phones and embedded electronics.
In order to simplify the networks, Professor Zhang tries to introduce simple, efficient, and accurate approximations to CNNs by binarizing the weights. Professor Zhang needs your help.
More specifically, you are given a weighted vector 
. Professor Zhang would like to find a binary vector
(bi∈{+1,−1}) and a scaling factor α≥0 in such a manner that
is minimum.
Note that 
denotes the Euclidean norm (i.e.
, where X=(x1,x2,...,xn)).
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains an integers n (1≤n≤100000) -- the length of the vector. The next line contains n integers: w1,w2,...,wn (−10000≤wi≤10000).
Output
For each test case, output the minimum value of as an irreducible fraction "p/q" where p, q are integers, q>0.
Sample Input
4
1 2 3 4
4
2 2 2 2
5
5 6 2 3 4
Sample Output
0/1
10/1
Problem Idea
解题思路:
【题意】
给你一个加权向量,需要我们找到一个二进制向量和一个比例因子α,使得最小
运算:
【类型】
暴力
【分析】
首先,观察下列式子
我们可以得到此题要我们求解的式子
等式右边有没有一种熟悉的感觉
没错,很想方差公式,但是还有些许出入,我们知道,要使方差最小,α需要取w1,w2,……,wn的平均数
而二进制向量的存在,则是进一步减小平均值,只需要对所有的wi取绝对值,那么新得到的平均值会小于等于原先的平均数
比如,当wi<0时,此时只需把bi取为负,那么就和wi>0时,bi取为正等价了
好了,现在我们已经定好了二进制向量和比例因子
那么可以对原式进行化简
然后,因为wi的值是已给的,那上述结果即为所求
其实一开始的时候,博主并不是用这种方法做的,而是采取下列这种方法:
有了公式之后,就循环求解每一项了,然而却一直WA,表示不是很明白,公式也是成立的,为什么就会WA呢
最后得出结论,可能是中间过程超过了__int64的大小,ORZ,错了n发
【时间复杂度&&优化】
O(nT)
题目链接→HDU 5734 Acperience
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1005 Eureka
Accept: 0 Submit: 0
Time Limit: 8000/4000 MS (Java/Others) Memory Limit : 65536/65536K (Java/Others)
Problem Description
A set P (P contains the label of the points) is called best set if and only if there are at least one best pair in P. Two numbers u and v (u,v∈P,u≠v) are called best pair, if for every w∈P, f(u,v)≥g(u,v,w), where
and
.
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains an integer n (1≤n≤1000) -- then number of points.
Each of the following n lines contains two integers xi and yi (−10^9≤xi,yi≤10^9) -- coordinates of the i-th point.
Output
For each test case, output an integer denoting the answer.
Sample Input
3
1 1
1 1
1 1
3
0 0
0 1
1 0
1
0 0
Sample Output
3
0
Problem Idea
解题思路:
【题意】
给你n个点的坐标,求符合条件的best sets有几个
【类型】
几何+有序化思想
【分析】
一个点集P是best sets当且仅当该点集至少包含一对best pair
而一对点{u,v}是best pair当且仅当该点集P中的任意一点w均满足f(u,v)≥g(u,v,w)
所以我们首先要对不等式进行化简
再看函数f(u,v)
由公式可以看出f(u,v)表示点u和点v之间的距离
那么不等式的含义就是:两边之和小于等于第三边?显然,这与三角形的定理是相矛盾的,由此可以得出,一个best sets就是该点集内所有点共线
就这么巧妙的,题目转化了,就是问,给你n个点的坐标,求有多少个不同的点集,满足点集内的所有点共线
比赛的时候判断共线采用的是将两点确定的直线y=kx+b的斜率k和截距b作为map的键值保存在map中,值则是该直线上的点数,时间复杂度是O(n^2logn),然而却是TLE,据说是因为卡常数
而暂且抛开TLE不说,其实这想法就算不卡常数,也能被精度吊死,毕竟斜率k和截距b都是double类型
也罢,换种想法,判断共线可以以向量形式进行存储
对于以点u作为起点,u(x1,y1)->v(x2,y2)的向量坐标为ξ(x2-x1,y2-y1)
对于以点u作为起点,u(x1,y1)->w(x3,y3)的向量坐标为υ(x3-x1,y3-y1)
因为有共同的起点,向量共线其实就是两向量之间存在一定的比例因子k,满足ξ=kυ,那我们不妨将坐标化简,这样所有共线的末点就被压缩至了一点
压缩后的向量坐标:ξ((x2-x1)/k,(y2-y1)/k),k为(x2-x1)与(y2-y1)的最大公约数,向量υ的坐标同理
假设起点u重点个数为cnt个,除点u以外与u共线的点有knt个
那么,该直线上满足条件的点集个数为
具体见代码,有不懂的地方再问
【时间复杂度&&优化】
O(n^2logn)
题目链接→HDU 5738 Eureka
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1009 It's All In The Mind
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536K (Java/Others)
Problem Description
Professor Zhang has a number sequence a1,a2,...,an. However, the sequence is not complete and some elements are missing. Fortunately, Professor Zhang remembers some properties of the sequence:
1. For every i∈{1,2,...,n}, 0≤ai≤100.
2. The sequence is non-increasing, i.e. a1≥a2≥...≥an.
3. The sum of all elements in the sequence is not zero.
Professor Zhang wants to know the maximum value of 
among all the possible sequences.
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first contains two integers n and m (2≤n≤100,0≤m≤n) -- the length of the sequence and the number of known elements.
In the next m lines, each contains two integers xi and yi (1≤xi≤n,0≤yi≤100,xi
Output
For each test case, output the answer as an irreducible fraction "p/q", where p, q are integers, q>0.
Sample Input
2 0
3 1
3 1
Sample Output
200/201
Problem Idea
解题思路:
【题意】
有一个非递增序列,其每个元素的取值为0~100,现在已知其中的m项元素值,求的最大值
【类型】
数学
【分析】
对于式子
显然,可以看成如下形式
再简化一点
这时,我们可以发现,当a值一定时,b值越小,整体结果越大,因为b越小,整体越趋近于1
就像1/(1+4)<1/(1+3)<1/(1+2)
当b值固定时,a越大,整体结果越大,显然,a值越大,b在a+b中所占的比例越小,整体越趋近于1
如2/(2+1)<3/(3+1)<4/(4+1)
所以,我们从序列尾部开始赋值,尽可能赋小,而前两项赋大,当然,已经知道的项,要确保其前面的未知项要等于该项,这样问题就解决了
【时间复杂度&&优化】
O(nT)
题目链接→HDU 5742 It's All In The Mind
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1011 Keep On Movin
Accept: 0 Submit: 0
Time Limit: 4000/2000 MS (Java/Others) Memory Limit : 65536/65536K (Java/Others)
Problem Description
Professor Zhang has kinds of characters and the quantity of the i-th character is ai. Professor Zhang wants to use all the characters build several palindromic strings. He also wants to maximize the length of the shortest palindromic string.
For example, there are 4 kinds of characters denoted as 'a', 'b', 'c', 'd' and the quantity of each character is {2,3,2,2} . Professor Zhang can build {"acdbbbdca"}, {"abbba", "cddc"}, {"aca", "bbb", "dcd"}, or {"acdbdca", "bb"}. The first is the optimal solution where the length of the shortest palindromic string is 9.
Note that a string is called palindromic if it can be read the same way in either direction.
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains an integer n (1≤n≤10^5) -- the number of kinds of characters. The second line contains n integers a1,a2,...,an (0≤ai≤10^4).
Output
Sample Input
4
1 1 2 4
3
2 2 2
5
1 1 1 1 1
5
1 1 2 2 3
Sample Output
6
1
3
Problem Idea
解题思路:
【题意】
n种字符,每种ai个,现要将这些字符全用来构成回文串,问所构成的回文串中最小的那串的长度的最大值为多少
【类型】
奇偶性判断
【分析】
首先,奇数个的字符种类数决定了回文串的个数
因为该字符必须放置在回文串的正中间
若无奇数个的字符,则可以构成一整串字符串,长度为总字符数
由于奇数个字符组成的字符串长度必定为奇数长,所以(总字符数/回文串数)为偶数时,最短的回文串长为(总字符数/回文串数-1)
【时间复杂度&&优化】
O(nT)
题目链接→HDU 5744 Keep On Movin
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include Problem 1012 La Vie en rose
Accept: 0 Submit: 0
Time Limit: 14000/7000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Problem Description
Professor Zhang would like to solve the multiple pattern matching problem, but he only has only one pattern string p=p1p2...pm. So, he wants to generate as many as possible pattern strings from p using the following method:
1. select some indices i1,i2,...,ik such that 1≤i1
Now, for a given a string s=s1s2...sn, Professor Zhang wants to find all occurrences of all the generated patterns in s.
Input
The first line contains two integers n and m (1≤n≤10^5,1≤m≤min{5000,n}) -- the length of s and p.
The second line contains the string s and the third line contains the string p. Both the strings consist of only lowercase English letters.
Output
Sample Input
4 1
abac
a
4 2
aaaa
aa
9 3
abcbacacb
abc
Sample Output
1110
100100100
Problem Idea
解题思路:
【题意】
字符串s与字符串p,从字符串p中选取k个互不相邻的字符,将其与各自右边的那个字符交换得到新的模式串,将这些模式串与字符串s进行匹配
匹配正确的位置记为1,否则记为0
【类型】
据说DP,然后竟然暴力过了
【分析】
一开始的时候着实被这题的正确率惊吓到了,然而却没有任何想法,如果愣是把p可能转化的模式串全找出来在用AC自动机,感觉有点爆炸
所以应该换个方向,去鼓捣字符串s
然后万万没想到竟然能够暴力过
对于从si位置开始的字符串s,与p串进行一一匹配,或交叉匹配(因为有交换操作),若整串匹配成功,则在位置i标记1,否则标记0
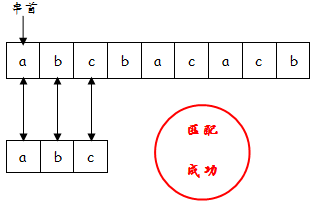
为了便于理解,我们对样例3的匹配过程进行模拟
①以s[0]为串首进行匹配时,直接匹配成功
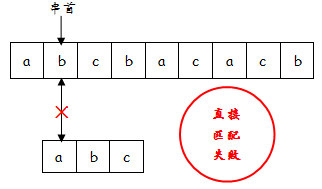
②以s[1]为串首进行匹配时,直接匹配失败,因为'b'!='a'
交叉匹配也失败,因为'c'!='a'
③同理,以s[2]为串首时,匹配也是失败的
④当以s[3]为串首时,交叉匹配成功
据大神说,此题可以篡改KMP的next数组进行匹配,然而本人目前并不知道如何修改
【时间复杂度&&优化】
O(mnT)
题目链接→HDU 5745 La Vie en rose
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include
#include
#include
#include
#include
#include
#include
#include