一文搞懂交叉熵损失

本文从信息熵和最大似然估计来推导交叉熵作为分类损失的依据。

从熵来看交叉熵损失

信息量

信息量来衡量一个事件的不确定性，一个事件发生的概率越大，不确定性越小，则其携带的信息量就越小。

设$X$是一个离散型随机变量，其取值为集合$X=x_0,x_1,\dots ,x_n$ ，则其概率分布函数为$p(x)=Pr(X=x),x\in X$，则定义事件$X=x_0$ 的信息量为：
$$I(x_0)=-\log (p(x_0))$$
当$p(x_0)=1$时，该事件必定发生，其信息量为0.

熵

熵用来衡量一个系统的混乱程度，代表系统中信息量的总和；熵值越大，表明这个系统的不确定性就越大。

信息量是衡量某个事件的不确定性，而熵是衡量一个系统（所有事件）的不确定性。

熵的计算公式
$$H(x)=-\sum _{i=1}^{n}p(x_i)\log (p(x_i))$$
其中，$p(x_i)$为事件$X=x_i$的概率，$-log(p(x_i))$为事件$X=x_i$的信息量。

可以看出，熵是信息量的期望值，是一个随机变量（一个系统，事件所有可能性）不确定性的度量。熵值越大，随机变量的取值就越难确定，系统也就越不稳定；熵值越小，随机变量的取值也就越容易确定，系统越稳定。

相对熵 Relative entropy

相对熵也称为KL散度(Kullback-Leibler divergence)，表示同一个随机变量的两个不同分布间的距离。

设 $p(x),q(x)$ 分别是 离散随机变量$X$的两个概率分布，则$p$对$q$的相对熵是：
$$D_{KL}(p\parallel q)=\sum _{i}p(x_i)log(\frac{p(x_i)}{q(x_i)})$$

相对熵具有以下性质：

• 如果$p(x)$和$q(x)$的分布相同，则其相对熵等于0
• $D_{KL}(p\parallel q)\ne D_{KL}(q\parallel p)$，也就是相对熵不具有对称性。
• $D_{KL}(p\parallel q)\ge 0$

总的来说，相对熵是用来衡量同一个随机变量的两个不同分布之间的距离。在实际应用中，假如$p(x)$是目标真实的分布，而$q(x)$是预测得来的分布，为了让这两个分布尽可能的相同的，就需要最小化KL散度。

交叉熵 Cross Entropy

设 $p(x),q(x)$ 分别是 离散随机变量$X$的两个概率分布，其中$p(x)$是目标分布，$p$和$q$的交叉熵可以看做是，使用分布$q(x)$ 表示目标分布$p(x)$的困难程度：
$$H(p,q)=\sum _{i}p(x_i)log\frac{1}{\log q(x_i)}=-\sum _{i}p(x_i)\log q(x_i)$$
将熵、相对熵以及交叉熵的公式放到一起，
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ H(p) &= -\sum_…
通过上面三个公式就可以得到
$$D_{KL}(p,q)=H(p,q)-H(p)$$
在机器学习中，目标的分布$p(x)$ 通常是训练数据的分布是固定，即是$H(p)$ 是一个常量。这样两个分布的交叉熵$H(p,q)$ 也就等价于最小化这两个分布的相对熵$D_{KL}(p\parallel q)$。

设$p(x)$ 是目标分布（训练数据的分布），我们的目标的就让训练得到的分布$q(x)$尽可能的接近$p(x)$，这时候就可以最小化$D_{KL}(p\parallel q)$，等价于最小化交叉熵$H(p,q)$ 。

从最大似然看交叉熵

设有一组训练样本$X=\{x_1,x_2,\cdots ,x_m\}$ ,该样本的分布为$p(x)$ 。假设使用$\theta$ 参数化模型得到$q(x;\theta )$ ，现用这个模型来估计$X$ 的概率分布，得到似然函数
$$L(\theta )=q(X;\theta )=\prod _i^{m}q(x_i;\theta )$$
最大似然估计就是求得$\theta$ 使得$L(\theta )$ 的值最大，也就是
$${\theta }_{ML}=arg\underset{\theta }{\max }\prod _i^{m}q(x_i;\theta )$$
对上式的两边同时取$\log$ ，等价优化$\log$ 的最大似然估计即log-likelyhood ，最大对数似然估计
$${\theta }_{ML}=arg\underset{\theta }{\max }\sum _i^m\log q(x_i;\theta )$$
对上式的右边进行缩放并不会改变$arg\max$ 的解，上式的右边除以样本的个数$m$
$${\theta }_{ML}=arg\underset{\theta }{\max }\frac{1}{m}\sum _i^m\log q(x_i;\theta )$$

和相对熵等价

上式的最大化${\theta }_{ML}$ 是和没有训练样本没有关联的，就需要某种变换使其可以用训练的样本分布来表示，因为训练样本的分布可以看作是已知的，也是对最大化似然的一个约束条件。

注意上式的
$$\frac{1}{m}\sum _i^m\log q(x_i;\theta )$$
相当于求随机变量$X$ 的函数$\log (X;\theta )$ 的均值 ，根据大数定理，随着样本容量的增加，样本的算术平均值将趋近于随机变量的期望。 也就是说
$$\frac{1}{m}\sum _i^m\log q(x_i;\theta )\to E_{x\sim P}(\log q(x;\theta ))$$
其中$E_{X\sim P}$ 表示符合样本分布$P$ 的期望，这样就将最大似然估计使用真实样本的期望来表示
$$\begin{array}{rl}{\theta }_{ML}& =arg\underset{\theta }{\max }{E}_{x\sim P}(\log q(x;\theta ))\\ & =arg\underset{\theta }{\min }{E}_{x\sim P}(-\log q(x;\theta ))\end{array}$$
对右边取负号，将最大化变成最小化运算。

上述的推导过程，可以参考 《Deep Learning》 的第五章。 但是，在书中变为期望的只有一句话，将式子的右边除以样本数量$m$ 进行缩放，从而可以将其变为$E_{x\sim p}\log q(x;\theta )$，没有细节过程，也可能是作者默认上面的变换对读者是一直。 确实是理解不了，查了很多文章，都是对这个变换的细节含糊其辞。一个周，对这个点一直耿耿于怀，就看了些关于概率论的科普书籍，其中共有介绍大数定理的：当样本容量趋于无穷时，样本的均值趋于其期望。

针对上面公式，除以$m$后，$\frac{1}{m}{\sum }_i^m\log q(x_i;\theta )$ ，确实是关于随机变量函数$\log q(x)$ 的算术平均值，而$x$ 是训练样本其分布是已知的$p(x)$ ，这样就得到了$E_{x\sim p}(\log q(x))$ 。

$$\begin{array}{rl}{D}_{KL}(p\parallel q)& =\sum _{i}p(x_i)log(\frac{p(x_i)}{q(x_i)})\\ & =E_{x\sim p}(\log \frac{p(x)}{q(x)})\\ & =E_{x\sim p}(\log p(x)-\log q(x))\\ & =E_{x\sim p}(\log p(x))-E_{x\sim p}(\log q(x))\end{array}$$

由于$E_{x\sim p}(\log p(x))$ 是训练样本的期望，是个固定的常数，在求最小值时可以忽略，所以最小化$D_{KL}(p\parallel q)$ 就变成了最小化$-E_{x\sim p}(\log q(x))$ ，这和最大似然估计是等价的。

和交叉熵等价

最大似然估计、相对熵、交叉熵的公式如下
$$\begin{array}{rl}{\theta }_{ML}& =-arg\underset{\theta }{\min }{E}_{x\sim p}\log q(x;\theta )\\ D_{KL}& =E_{x\sim p}\log p(x)-E_{x\sim p}\log q(x)\\ H(p,q)& =-\sum _i^{m}p(x_i)\log q(x_i)=-E_{x\sim p}\log q(x)\end{array}$$
从上面可以看出，最小化交叉熵，也就是最小化$D_{KL}$ ，从而预测的分布$q(x)$ 和训练样本的真实分布$p(x)$ 最接近。而最小化$D_{KL}$ 和最大似然估计是等价的。

多分类交叉熵

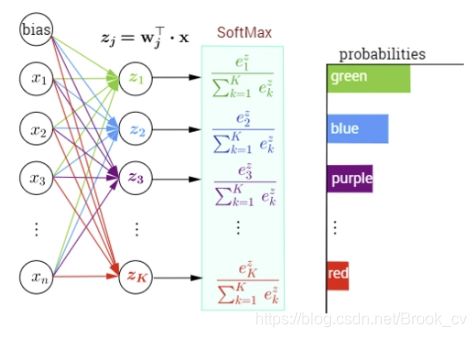
多分类任务中输出的是目标属于每个类别的概率，所有类别概率的和为1，其中概率最大的类别就是目标所属的分类。 而softmax 函数能将一个向量的每个分量映射到$[0,1]$ 区间，并且对整个向量的输出做了归一化，保证所有分量输出的和为1，正好满足多分类任务的输出要求。所以，在多分类中，在最后就需要将提取的到特征经过softmax函数的，输出为每个类别的概率，然后再使用交叉熵 作为损失函数。

softmax函数定义如下：
$$S_i=\frac{e^{z_i}}{{\sum }_{i=1}^n{e}^{z_i}}$$
其中，输入的向量为$z_i(i=1,2,\dots ,n)$ 。

更直观的参见下图

通过前面的特征提取到的特征向量为$(z_1,z_2,\dots ,z_k)$ ，将向量输入到softmax函数中，即可得到目标属于每个类别的概率，概率最大的就是预测得到的目标的类别。

Cross Entropy Loss

使用softmax函数可以将特征向量映射为所属类别的概率，可以看作是预测类别的概率分布$q(c_i)$ ，有
$$q(c_i)=\frac{e^{z_i}}{{\sum }_{i=1}^n{e}^{z_i}}$$

其中$c_i$ 为某个类别。

设训练数据中类别的概率分布为$p(c_i)$ ，那么目标分布$p(c_i)$ 和预测分布$q(c_i)$的交叉熵为
$$H(p,q)=-\sum _{i}p(c_i)\log q(c_i)$$
每个训练样本所属的类别是已知的，并且每个样本只会属于一个类别（概率为1），属于其他类别概率为0。具体的，可以假设有个三分类任务，三个类分别是：猫，猪，狗。现有一个训练样本类别为猫，则有：
$$\begin{array}{rl}p(cat)& =1\\ p(pig)& =0\\ p(dog)& =0\end{array}$$

通过预测得到的三个类别的概率分别为：$q(cat)=0.6,q(pig)=0.2,q(dog)=0.2$ ，计算$p$ 和$q$ 的交叉熵为：
$$\begin{array}{rl}H(p,q)& =-(p(cat)\log q(cat)+p(pig)+\log q(pig)+\log q(dog))\\ & =-(1\cdot \log 0.6+0\cdot \log 0.2+0\cdot \log 0.2)\\ & =-\log 0.6\\ & =-\log q(cat)\end{array}$$
利用这种特性，可以将样本的类别进行重新编码，就可以简化交叉熵的计算，这种编码方式就是one-hot 编码。以上面例子为例，
$$\begin{array}{rl}\text{cat}& =(100)\\ \text{pig}& =(010)\\ \text{dog}& =(001)\end{array}$$
通过这种编码方式，在计算交叉熵时，只需要计算和训练样本对应类别预测概率的值，其他的项都是$0\cdot \log q(c_i)=0$ 。

具体的，交叉熵计算公式变成如下：
$$\text{Cross\_Entropy}(p,q)=-\log q(c_i)$$
其中$c_i$ 为训练样本对应的类别，上式也被称为负对数似然（negative log-likelihood,nll）。

PyTorch中的Cross Entropy

PyTorch中实现交叉熵损失的有三个函数torch.nn.CrossEntropyLoss，torch.nn.LogSoftmax以及torch.nn.NLLLoss。

• torch.nn.functional.log_softmax 比较简单，输入为$n$维向量，指定要计算的维度dim，输出为$log(Softmax(x))$。其计算公式如下：
  $$\text{LogSoftmax}(x_i)=\log (\frac{\exp (x_i)}{{\sum }_j\exp (x_j)})$$
  没有额外的处理，就是对输入的$n$维向量的每个元素进行上述运算。

• torch.nn.functional.nll_loss 负对数似然损失（Negative Log Likelihood Loss)，用于多分类，其输入的通常是torch.nn.functional.log_softmax的输出值。其函数如下

torch.nn.functional.nll_loss(input, target, weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

input 也就是log_softmax的输出值，各个类别的对数概率。target 目标正确类别,weight 针对类别不平衡问题，可以为类别设置不同的权值；ignore_index 要忽略的类别，不参与loss的计算；比较重要的是reduction 的值，有三个取值：none 不做处理，输出的结果为向量；mean 将none结果求均值后输出；sum 将none 结果求和后输出。

• torch.nn.CrossEntropyLoss就是上面两个函数的组合nll_loss(log_softmax(input))。

二分类交叉熵

多分类中使用softmax函数将最后的输出映射为每个类别的概率，而在二分类中则通常使用sigmoid 将输出映射为正样本的概率。这是因为二分类中，只有两个类别：{正样本，负样本}，只需要求得正样本的概率$q$,则$1-q$ 就是负样本的概率。这也是多分类和二分类不同的地方。

$\text{sigmoid}$ 函数的表达式如下：
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
sigmoid的输入为$z$ ，其输出为$(0,1)$ ，可以表示分类为正样本的概率。

二分类的交叉熵可以看作是交叉熵损失的一个特列，交叉熵为
$$\text{Cross\_Entropy}(p,q)=-\sum _i^{m}p(x_i)\log q(x_i)$$
这里只有两个类别$x\in x_1,x_2$ ，则有
$$\begin{array}{rl}\text{Cross\_Entropy}(p,q)& =-(p(x_1)\log q(x_1)+p(x_2)\log q(x_2))\end{array}$$
因为只有两个选择，则有$p(x_1)+p(x_2)=1,q(x_1)+q(x_2)=1$ 。设，训练样本中$x_1$的概率为$p$，则$x_2$为$1-p$; 预测的$x_1$的概率为$q$，则$x_2$的预测概率为$1-q$ 。则上式可改写为
$$\text{Cross\_Entropy}(p,q)=-(p\log q+(1-p)\log (1-q))$$
也就是二分类交叉熵的损失函数。

总结

相对熵可以用来度量两个分布相似性，假设分布$p$是训练样本的分布，$q$是预测得到的分布。分类训练的过程实际上就是最小化$D_{KL}(p\parallel q)$，由于由于交叉熵
$$H(p,q)=D_{KL}(p\parallel q)+H(p)$$
其中,$H(p)$是训练样本的熵，是一个已知的常量，这样最小化相对熵就等价于最小化交叉熵。

从最大似然估计转化为最小化负对数似然
$${\theta }_{ML}=-arg\underset{\theta }{\min }{E}_{x\sim p}\log q(x;\theta )$$
也等价于最小化相对熵。