HDU 1198 Farm Irrigation (并查集 和 dfs两种实现)
Farm Irrigation
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 4977 Accepted Submission(s): 2137
Problem Description
Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.
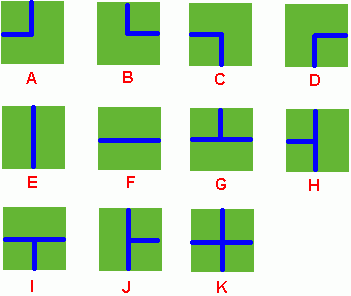
Figure 1
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
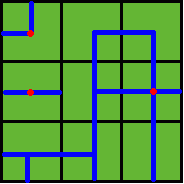
Figure 2
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map
ADC
FJK
IHE
then the water pipes are distributed like
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.
Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?
Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.
Input
There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.
Output
For each test case, output in one line the least number of wellsprings needed.
Sample Input
2 2 DK HF 3 3 ADC FJK IHE -1 -1
Sample Output
2 3
题意:有如上图11种土地块,块中的绿色线条为土地块中修好的水渠,现在一片土地由上述的各种土地块组成,需要浇水,问需要打多少口井。
例如下面这个土地块
ADC
FJK
IHE
then the water pipes are distributed like
#include
#include
#include
const int MAX = 550;
//存储11中类型的土地,二维中的0 1 2 3分别代表这种类型的土地的左上右下
//为1表示这个方向有接口,为0表示这个方向没有接口
const int type[11][4]={{1,1,0,0},{0,1,1,0},
{1,0,0,1},{0,0,1,1},
{0,1,0,1},{1,0,1,0},
{1,1,1,0},{1,1,0,1},
{1,0,1,1},{0,1,1,1},
{1,1,1,1}
};
const bool VERTICAL = true;
//pre数组就是正常的并查集中所用,但是在合并的时候要注意将二维坐标转换成一维的标号,此处用行优先
int pre[MAX*MAX+1],cnt,m,n;
char farm[MAX][MAX];
void init(int n){
int i;
for(i=1;i<=n;++i){
pre[i] = i;
}
cnt = n;
}
int root(int x){
if(x!=pre[x]){
pre[x] = root(pre[x]);
}
return pre[x];
}
void merge(int ax,int ay,int bx,int by,bool dir){
if(bx>n || by>m)return;//超出地图的部分不进行合并
bool mark = false;//标识两块地是否可连
int ta,tb;//两点的类型值0-10
ta = farm[ax][ay]-'A';
tb = farm[bx][by]-'A';
if(dir){//竖直方向判断可连性
if(type[ta][3] && type[tb][1])mark = true;
}else{//水平方向判断可连性
if(type[ta][2] && type[tb][0])mark = true;
}
if(mark){//只要可连就合并,这就是正常的并查集了
int fx = root((ax-1)*m+ay);
int fy = root((bx-1)*m+by);
if(fx!=fy){
pre[fy] = fx;
--cnt;
}
}
}
int main(){
//freopen("in.txt","r",stdin);
int i,j;
while(scanf("%d %d",&n,&m)!=EOF){
if(n==-1 && m==-1)break;
init(n*m);
for(i=1;i<=n;++i){
scanf("%s",farm[i]+1);
}
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
merge(i,j,i+1,j,VERTICAL);
merge(i,j,i,j+1,!VERTICAL);
}
}
printf("%d\n",cnt);
}
return 0;
}
#include
#include
#include
const int MAX = 550;
const int type[11] = {3,6,9,12,10,5,7,11,13,14,15};
const bool VERTICAL = true;
//pre数组就是正常的并查集中所用,但是在合并的时候要注意将二维坐标转换成一维的标号,此处用行优先
int pre[MAX*MAX+1],cnt,m,n;
char farm[MAX][MAX];
void init(int n){
int i;
for(i=1;i<=n;++i){
pre[i] = i;
}
cnt = n;
}
int root(int x){
if(x!=pre[x]){
pre[x] = root(pre[x]);
}
return pre[x];
}
void merge(int ax,int ay,int bx,int by,bool dir){
if(bx>n || by>m)return;//超出地图的部分不进行合并
bool mark = false;//标识两块地是否可连
int ta,tb;//两点的类型值0-10
ta = farm[ax][ay]-'A';
tb = farm[bx][by]-'A';
if(dir){//竖直方向判断可连性
if(((type[ta]>>3) & 1) && ((type[tb]>>1) & 1))mark = true;
}else{//水平方向判断可连性
if(((type[ta]>>2) & 1) && (type[tb] & 1))mark = true;
}
if(mark){//只要可连就合并,这就是正常的并查集了
int fx = root((ax-1)*m+ay);
int fy = root((bx-1)*m+by);
if(fx!=fy){
pre[fy] = fx;
--cnt;
}
}
}
int main(){
//freopen("in.txt","r",stdin);
int i,j;
while(scanf("%d %d",&n,&m)!=EOF){
if(n==-1 && m==-1)break;
init(n*m);
for(i=1;i<=n;++i){
scanf("%s",farm[i]+1);
}
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
merge(i,j,i+1,j,VERTICAL);
merge(i,j,i,j+1,!VERTICAL);
}
}
printf("%d\n",cnt);
}
return 0;
}
#include
#include
#include
#include
const int MAX = 550;
const int type[11] = {3,6,9,12,10,5,7,11,13,14,15};
const int dirx[4] = {0,-1,0,1},diry[4]={-1,0,1,0};
int m,n;
char farm[MAX][MAX];
int visit[MAX][MAX];
bool yes(int ax,int ay,int bx,int by,int dir){
bool mark = false;
int ta,tb;
if(bx<1 || bx>n || by<1 || by>m)return false;
ta = farm[ax][ay]-'A';
tb = farm[bx][by]-'A';
if(dir==0){//向左
if((type[ta] & 1) && ((type[tb]>>2) & 1))mark = true;
}else if(dir==1){//向上判断可连性
if(((type[ta]>>1) & 1) && ((type[tb]>>3) & 1))mark = true;
}else if(dir==2){//水平向右
if(((type[ta]>>2) & 1) && (type[tb] & 1))mark = true;
}else{//水平向下判断可连性
if(((type[ta]>>3) & 1) && ((type[tb]>>1) & 1))mark = true;
}
return mark;
}
void dfs(int x,int y){
if(visit[x][y])return;
visit[x][y] = 1;
int tx,ty,i;
for(i=0;i<4;++i){
tx = x + dirx[i];
ty = y + diry[i];
if(yes(x,y,tx,ty,i)){
dfs(tx,ty);
}
}
}
int main(){
//freopen("in.txt","r",stdin);
int i,j,ans;
while(scanf("%d %d",&n,&m)!=EOF){
if(n==-1 && m==-1)break;
ans = 0;
memset(visit,0,sizeof(visit));
for(i=1;i<=n;++i){
scanf("%s",farm[i]+1);
}
for(i=1;i<=n;++i){
for(j=1;j<=m;++j){
if(visit[i][j])continue;
++ans;
dfs(i,j);
}
}
printf("%d\n",ans);
}
return 0;
}