PyTorch入门实战教程笔记(十三):梯度相关操作4
PyTorch入门实战教程笔记(十三):梯度相关操作4
MLP反向传播
在前面介绍我们了解到,对于多层感知机误差E对Wjk的偏导为(Ok-tk)Ok(1 - Ok)x0j , 如果前面在添加一层,其输出为OjJ ,那么 误差E对Wjk的偏导为(Ok-tk)Ok(1 - Ok)Oj J。如下图:
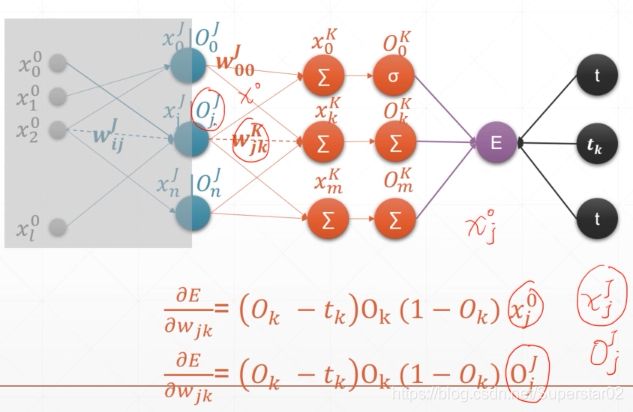
那么对于多层的感知机MLP,链式求导详细推导如下图:下图第5行运用链式法则来求导,最终结果如红框所示,Oi即图中的xi,这样写为了表达Oi为前一层的输出。
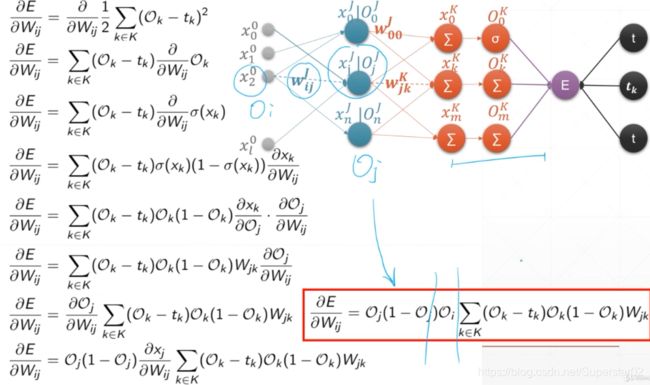
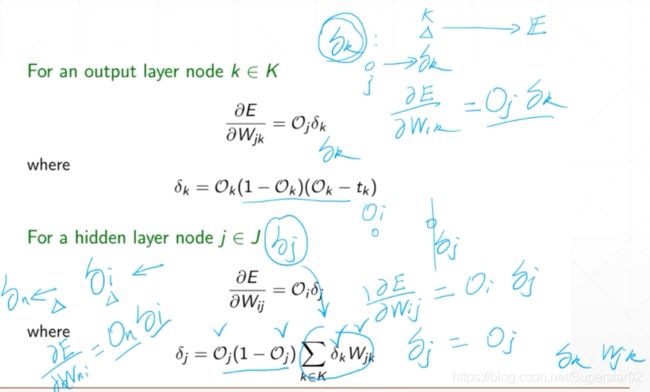
下面,我们对上述公式详细分析简化并推导,E对Wjk的偏导等于Ok(1 - Ok)(Ok-tk)Oj 。令δk = Ok(1 - Ok)(Ok-tk),那么E对Wjk的偏导就等于Oj δk,那么E对Wij的偏导就等于OiOj(1 - Oj)ΣδkWjk,令δj = Oj(1 - Oj)ΣδkWjk,那么E对Wij的偏导就等于Oiδj ,上述的W,O都是已知的,然后通过反复迭代,就能求出再前一层δi,再再前一层的δn等等,这样就能反向传播求出E对所有层的W的偏导数,进而求得各W的梯度,来更新W,不停的更新W,直到权值W到达我们想要的程度。如下图:
2D函数优化实例
给定下面的函数Himmelblau function:科学家找到这样一个函数,通过这种可视化的示例函数,看看设计的优化器能不能找到优化的解。
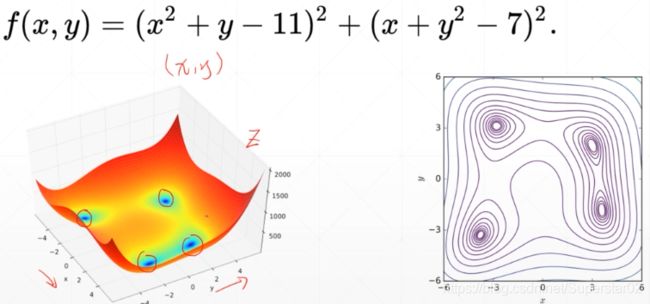
函数的四个解如下:

首先我们将该函数实现出来并可视化出来:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import torch
def himmelblau(x):
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y) #将(x,y)值传进去,并生成相应的坐标
print('X,Y maps:', X.shape, Y.shape) #输出为(120,120),(120,120)
Z = himmelblau([X, Y])
#绘图
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
结果如下图:
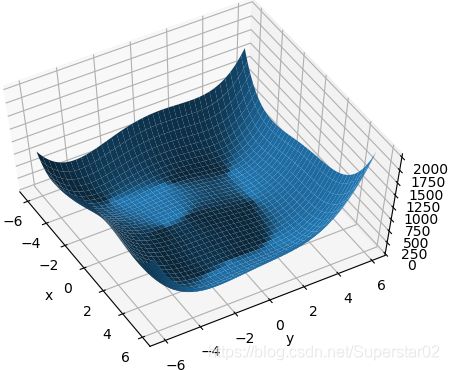
通过优化器优化这个函数,注意,我们优化的是预测值和x,而不是error的E和权值W,代码如下:
# [1., 0.], [-4, 0.], [4, 0.]
x = torch.tensor([-4., 0.], requires_grad=True)
#优化器自动完成x[0],x[1](即x,y)的梯度更新,
#x' = x - lr▽x,y' = y - lr▽y
optimizer = torch.optim.Adam([x], lr=1e-3)
for step in range(20000):
pred = himmelblau(x) #预测值z应该等于真实值
optimizer.zero_grad() #将梯度信息清零,否则会叠加
pred.backward()
optimizer.step() #更新一次x' = x - lr▽x,y' = y - lr▽y
if step % 2000 == 0:
print ('step {}: x = {}, f(x) = {}'
.format(step, x.tolist(), pred.item()))
运算结果:
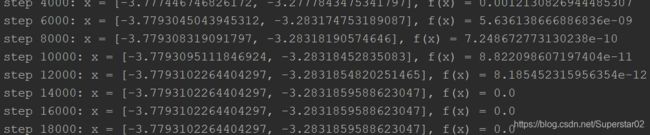
当我们改变初始x为x = torch.tensor([1., 0.], requires_grad=True),运算结果如下:
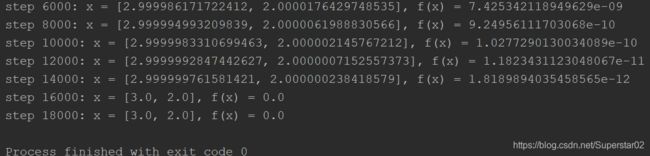
可以看到,不同的初始化,找到的局部最小值是不一样的,所以初始化是非常重要。