深度学习之Autoencoder及其在图像去噪上的应用

导言：“自编码器”（Autoencoder）是一种无监督的学习方法（更准确地用语应该是自监督），主要用于数据的降维或者特征的抽取。在作用上有点类似于PCA、字典学习，或者压缩感知。这里的数据降维，也可以理解为数据压缩，总之就是给高维的原始数据产生一个低维的表达，并要求这个低维表达最大程度地保持原始数据中的重要信息。可以类比于PCA中提取的主成分。但Autoencoder的压缩功能有三个特点：１）这种压缩是有损的；２）这种压缩或特征提取是针对特定数据的；３）这种压缩需要从数据中自动学习。另外，在几乎所有使用术语“自编码器”的语境下，数据压缩（包括解压缩）或特征提取都是通过神经网络实现的。

 

一、理论模型

更具体地说，我们有一些原始数据（通常是高维的），例如图像。然后用一个神经网络来对其进行压缩。这样的神经网络也被称为“编码器”（Encoder），原始数据经编码器处理后得到一个压缩的低维表达，如下图所示。

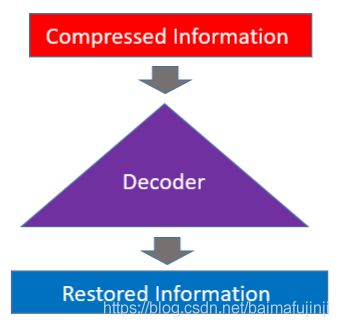
与编码器相对应的，还有“解码器”（Decoder），如下图所示。解码器也是一个神经网络，它把低维表达（也就是压缩后的信息）还原成与原始信息维度相同的复原信息。因为是有损压缩，所以这里的复原信息与原始信息是不会完全相同的。而我们所期望的是二者之间的差距尽可能地小。

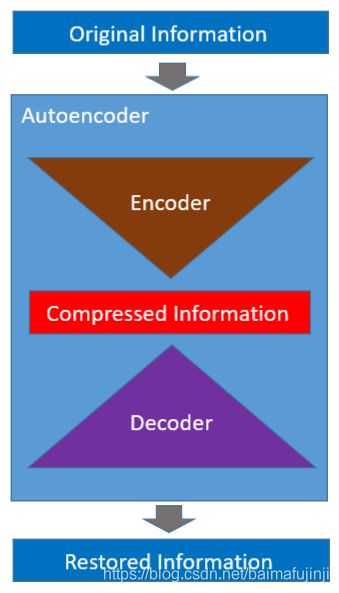
最后，把编码器和解码器整合起来，就得到了如下图所示的完整的Autoencoder框架。事实上，在神经网络训练阶段，编码器和解码器是同时构建的。这一点，在后面的实例中，也会看到。

假设，我们面对的原始数据是MNIST数据库中的一幅图像。可以知道，原始数据的维度有784。经过自编码器压缩后，数据可以降维到几十甚至更低。如下图所示，经过还原得到的图像仍然是可以辨识的。图像中绝大部分主要信息都得以保留。

但正如开篇导言中所所说的，这种基于自编码器的压缩有若干特点，这与传统意义上的压缩是存在区别的：

1. 自编码器是针对特定数据的，这意味着它们只能压缩那些同训练集中数据类似的数据。举例来说，传统的JPEG图像压缩算法可以通用于任何图像，而非特定类型的图像。但如果我们用于训练Autoencoder的数据集是MNIST，那么该Autoencoder就只能用来对这种手写数字产生低维表达。因此，在人脸图像上训练得到的自编码器如果用于压缩花草树木类图像，那么其表现可想而知是相当差的。
2. 自编码器是有损的，这意味着与原始输入相比，解压缩后得到的输出结果质量较原始数据相比会有所劣化（类似于MP3或JPEG压缩）。这与无损压缩方法（例如LZW编码算法）不同。
3. 自编码器是从数据实例中自动学习的，这是一个有用的属性：这意味着经特定数据集训练而得的模型将在特定类型的输入上表现良好。而且这样过程并不需要复杂的人工干预，后面给出的基于MNIST的实例会演示这一点。

要构建自编码器，您需要三件事：编码器，解码器，以及用于衡量原始数据与解压缩后的恢复数据之间信息丢失量的距离函数（即“损失”函数）。编码器和解码器通常都是神经网络，并且相对于距离函数是可微的，因此可以使用随机梯度下降等优化算法来求得编码/解码器的参数，以最大程度地减少重建损失。

二、一个问题

我们反复用到了压缩这个词，读者可能会问Autoencoder擅长数据压缩吗？或者说，它能用来取代传统的JPEG或者MP3算法吗？通常情况下答案是否定的。例如，在图片压缩中，很难训练出比JPEG等基本算法做得更好的自编码器。而且，Autoencoder的用武之地，通常需要限定处理的图像是非常特定的图片类型（而且是JPEG效果显然不佳时）。自编码器需要针对特定数据的事实使它们通常对于现实世界中的数据压缩问题不切实际，这也是我们反复强调的，你只能将它们用于与训练数据相似的数据上。如要使其更加通用，可能需要大量的训练数据。当然，或许未来随着技术的进步，这一点上可能会有所改善，当目前这仍然是它的一个局限。

三、自编码器的优点

自编码器的两个有趣的实际应用是数据去噪（我们将在本文后面的实例中加以演示）和用于数据可视化的降维。有了适当的尺寸和稀疏性约束，自编码器可以学习到比PCA或其他基本技术更有趣的数据映射。特别是对于2D可视化，t-SNE可能是已知的最好的算法，但它通常需要相对低维的数据。因此，可视化高维数据中相似关系的一种好策略是开始使用自编码器将数据压缩到低维空间（例如32维），然后再使用t-SNE将压缩后的数据映射到2D平面。

自编码器不是真正的无监督学习技术（这将意味着完全不同的学习过程），尽管它在训练时不需要“标签”，但更准确地说，它们是一种自监督技术，是从输入数据生成目标的有监督学习的特定实例。为了让自监督的模型学习到有意义的功能，你必须提出一个有意义的综合目标和损失函数，这就是问题的所在：仅学习细致地重建输入可能不是正确的选择（或者不是最好的选择）。试想一下，在准确地对输入进行重构中的同时，更能对我们感兴趣的主要任务（例如分类或定位等）上实现更高的性能或表现，岂不更好。更进一步，即使损失前者（也就是重构表现欠佳），但提取后的特征使得我们感兴趣的主要任务（例如分类或定位等）有较大突破，这或许才真应该是我们所追求的。

四、在MNIST上基于Keras完成的实例

下面以MNIST数据集为例，来演示Autoencoder的构建。在Keras上实现Autoencoder是非常容易的。首先，还是导入必要的包和数据集。

import keras
from keras.layers import Input, Dense
from keras.models import Model
from keras import regularizers

import matplotlib.pyplot as plt
%matplotlib inline

from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

作为一个简单的开始，我们采用最简单的单层全连接神经网络来作为编/解码器。优化器选择Adadelta，损失函数选择per-pixel binary crossentropy loss。经过编码器，原始784维的数据被压缩成了一个32维的数据。

# this is the size of our encoded representations
encoding_dim = 32  # 32 floats -> compression of factor 24.5, assuming the input is 784 floats

# this is our input placeholder
input_img = Input(shape=(784,))
# "encoded" is the encoded representation of the input
encoded = Dense(encoding_dim, activation='relu')(input_img)
# "decoded" is the lossy reconstruction of the input
decoded = Dense(784, activation='sigmoid')(encoded)

# this model maps an input to its reconstruction
autoencoder = Model(input_img, decoded)

# this model maps an input to its encoded representation
encoder = Model(input_img, encoded)

# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))
# retrieve the last layer of the autoencoder model
decoder_layer = autoencoder.layers[-1]
# create the decoder model
decoder = Model(encoded_input, decoder_layer(encoded_input))

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

训练模型50个epochs。

autoencoder.fit(x_train, x_train,
                epochs=50,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

最后，来展示一下原始图像与对应的恢复图像。

encoded_imgs = encoder.predict(x_test)
decoded_imgs = decoder.predict(encoded_imgs)

n = 10  # how many digits we will display
plt.figure(figsize=(20, 4))
for i in range(n):
    # display original
    ax = plt.subplot(2, n, i + 1)
    plt.imshow(x_test[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

    # display reconstruction
    ax = plt.subplot(2, n, i + 1 + n)
    plt.imshow(decoded_imgs[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

如下图所示，可见恢复后的图像很好地保持了原图中最重要的信息，同时，较原始图像而言，恢复后的图像质量有所劣化。

在前面的例子中，数据的低维表示仅仅限制于一个32维的向量，也就是说，我们只从向量维度这个角度对数据的低维表示做要求。这样做的通常结果是，神经网络的隐藏层仅仅学习到了一个与PCA相近似结果。除此之外，我们还可添加新的限制从而要求数据的低维表示满足稀疏性的要求。在Keras中，我们对Dense层添加一个activity_regularizer即可实现上述要求。

# add a Dense layer with a L1 activity regularizer
encoded = Dense(encoding_dim, activation='relu',
                activity_regularizer=regularizers.l1(10e-8))(input_img)

注意，在Keras中的官方教程【２】中，上述代码里使用的参数是10e-5，但经测试这样收敛的速度很慢，于是建议将其改为10e-8。即使这样，还是需要增加模型训练的epochs至100个。我个人测试的结果显示，训练loss和验证loss会分别收敛于0.101和0.996左右。下图给出的对比效果，显示添加了稀疏性限制之后的图像复原结果与之前给出的效果相比并无明显差异。但低维表示的稀疏性是有所增加的，这一点读者可以自己验证一下。

更进一步，还可以增加Dense层的层数，例如在构建编/解码器时，用下面的代码替换原程序中的对应代码：

# this is the size of our encoded representations
encoding_dim = 32  # 32 floats -> compression of factor 24.5, assuming the input is 784 floats

# this is our input placeholder
input_img = Input(shape=(784,))
encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(64, activation='relu')(encoded)
encoder_output = Dense(encoding_dim, activation='relu')(encoded)

decoded = Dense(64, activation='relu')(encoder_output)
decoded = Dense(128, activation='relu')(decoded)
decoded = Dense(784, activation='sigmoid')(decoded)

# this model maps an input to its reconstruction
autoencoder = Model(input_img, decoded)

# this model maps an input to its encoded representation
encoder = Model(input_img, encoder_output)

# autoencoder.summary()

# create a placeholder for an encoded (32-dimensional) input
encoded_input = Input(shape=(encoding_dim,))

# create the decoder model
deco = autoencoder.layers[-3](encoded_input)
deco = autoencoder.layers[-2](deco)
deco = autoencoder.layers[-1](deco)
# create the decoder model
decoder = Model(encoded_input, deco)

#decoder.summary()

autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

autoencoder.fit(x_train, x_train,
                epochs=100,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

需要注意的是decoder的实现部分，原始代码 works for single-layer because only last layer is decoder, for 3-layer encoders and decoders, you have to call all 3 layers for defining decoder。下面输出的重构结果显示增加网络隐藏层层数使得复原图像的质量有所提高。

注意到我们这里处理的是图像数据，前面一直使用的是全连接神经网络（Fully-connected NN），但实践中在处理图像时采用更多的是卷积神经网络（CNN）。于是下面，我们对之前的程序继续进行改写，转而采用CNN来构建Autoencoder。首先，还是读入必要的package以及数据集。由于接下来会采用CNN，所以这里数据维度转换的部分会跟之前代码的处理方式不同。

from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K

import matplotlib.pyplot as plt
%matplotlib inline

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))  # adapt this if using `channels_first` image data format
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))  # adapt this if using `channels_first` image data format

下面是神经网络结构构建的部分。注意在构建decoder的时候，我们使用了UpSampling2D，即上采样函数。其中的参数(2,2)分别给出了行放大倍数（这里取2的话代表原来的一行变成了两行，就是一行那么粗，变成了两行那么粗）和列放大倍数（这里取2的话代表原来的一列变成了两行，就是一列那么粗，变成了两列那么粗）。所以，(2,2)其实就等于将原图放大四倍（水平两倍，垂直两倍），例如32*32 变成 62*64的图像。

input_img = Input(shape=(28, 28, 1))  # adapt this if using `channels_first` image data format

x = Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)

# at this point the representation is (4, 4, 8) i.e. 128-dimensional

x = Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
x = Conv2D(16, (3, 3), activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)

# this model maps an input to its encoded representation
encoder = Model(input_img, encoded)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

train_history = autoencoder.fit(x_train, x_train,
                epochs=100,
                batch_size=128,
                shuffle=True,
                validation_data=(x_test, x_test))

在训练100个epochs之后，我们来看看重构结果与原始图像的对比效果。

decoded_imgs = autoencoder.predict(x_test)

n = 10
plt.figure(figsize=(20, 4))
for i in range(1, 10):
    # display original
    ax = plt.subplot(2, n, i)
    plt.imshow(x_test[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

    # display reconstruction
    ax = plt.subplot(2, n, i + n)
    plt.imshow(decoded_imgs[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

如下图所示，可见采用CNN的autoencoder可以得到更高质量的复原图像。

还可以可视化地展示训练历史中模型在训练集与验证集上loss的变化情况。

plt.plot(train_history.history['loss'])
plt.plot(train_history.history['val_loss'])
plt.title('Model Loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.show()

如下图所示，模型在训练集和验证集上最终的loss会收敛到0.1以下。

如果你有兴趣，还可以把图像的编码表达（encoded representations）绘制出来。前面的代码中已经指出，这个表达的维度是(4,4,8)，也就是总计 128维。为了把它以图像的形式绘制出来，这里将其转化成 4x32的灰度图像并做展示。

encoded_imgs = encoder.predict(x_test)

n = 10
plt.figure(figsize=(10, 4))
for i in range(n):
    ax = plt.subplot(1, n, i+1)
    plt.imshow(encoded_imgs[i].reshape(4, 4 * 8).T)
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

结果如下图所示。

最后，我们来见识一下Autoencoder的神奇的降噪能力。首先读入数据，并引入高斯噪声。

from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K

import matplotlib.pyplot as plt
%matplotlib inline

from keras.datasets import mnist
import numpy as np

(x_train, _), (x_test, _) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))  # adapt this if using `channels_first` image data format
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))  # adapt this if using `channels_first` image data format

noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape) 
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape) 

x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)

可以把带有噪声的图像绘制出来。

n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
    ax = plt.subplot(1, n, i+1)
    plt.imshow(x_test_noisy[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

可见，我们加入的噪声对图像影响较大，图像的质量已经严重劣化。

为了获得更好的效果，将之前的代码略作修改。注意，我们仍然采用CNN版的Autoencoder，但每个卷积层里设置更多的filters。

input_img = Input(shape=(28, 28, 1))  # adapt this if using `channels_first` image data format

x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D((2, 2), padding='same')(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D((2, 2), padding='same')(x)

# at this point the representation is (7, 7, 32)

x = Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)

autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')

train_history = autoencoder.fit(x_train_noisy, x_train,
                epochs=100,
                batch_size=128,
                shuffle=True,
                validation_data=(x_test_noisy, x_test))

由于Autoencoder是在没有噪声的MNIST数据集上训练出来的，所以它会更多地学到“干净”的手写数字图像特征。在利用已经训练好的模型进行图像重构时，输入有噪声的图像，Autoencoder会把它们尽量还原成跟训练数据集相近的样子（因为这是神经网络已经掌握和熟悉的知识）。于是，便起到了去噪的作用。

decoded_imgs = autoencoder.predict(x_test_noisy)

n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
    ax = plt.subplot(1, n, i+1)
    plt.imshow(decoded_imgs[i].reshape(28, 28))
    plt.gray()
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

下图是去噪后的效果图。注意，这是传统的去躁方法（高斯模糊、中值滤波、小波变换、JPEG去噪）都无法企及的效果！但是，但是，一定要注意，我们最开始讨论过的Autoencoder的限制，即它是data-specific的，也就是只能针对特定类型的数据。如果你用刚刚这个Autoencoder来一张含有噪声的花花草草图像做处理，是没有任何意义的。

最后需要补充的是，Autoencoder还有很多新的发展，例如基于LSTM的自编码器，有兴趣的读者不妨参考相关文献以了解更多。

 

*本文中所有的完整代码之Jupyter Notebook文件可以从【云盘链接】 下载得到（提取码: wvni）

---

 

参考文献

【１】How to reduce image noises by autoencoder　（文中部分示例图片引用自该文）

【２】Building Autoencoders in Keras　（文中部分示例图片和代码引用自该文，但示例中代码执行有误，笔者有修改）

【３】字典学习与图像去噪实践