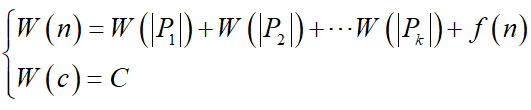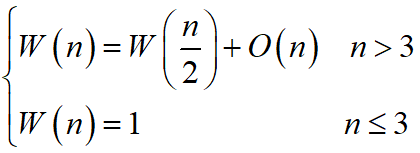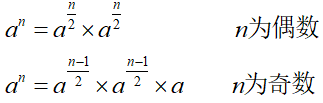分治策略

设 $P$ 是待求解的问题，$|P|$ 代表该问题的输入规模，一般的分治算法 Divide-and-Conquer 的伪码描述如下：

上述伪码说明：如果问题规模不超过 $c$，算法停止递归，直接求解 $P$，，Solve()就代表直接求解的过程；否则将 $P$ 规约成 $k$ 个彼此独立的子问题 $P_1,P_2,\cdots ,P_k$，然后递归地依次求解这些子问题，得到解 $y_1,y_2,\cdots ,y_k$；最后将 $k$ 个解归并得到原问题的解，Merge()代表归并子问题的解得过程.

根据上面伪代码，分治算法时间复杂度的递推方程的一般形式是：

观察上面递推方程，不难发现：如果子问题的规模都一样，方程得求解比较简单.

当子问题的划分比较均匀时，时间的复杂度也相对较低.

所以，分治算法的核心就是如何划分子问题，以及划分的正确性的证明！

---

【例 1】有 $n$ 片芯片，已知其中好芯片比坏芯片最少多 $1$ 片. 现在需要通过测试从中找出 $1$ 片好芯片. 测试的方法是：将 $2$ 片芯片放到测试台上，$2$ 片芯片互相测试并报告测试结果：”好“ 或者 ”坏“. 假定好芯片的报告是正确的，坏芯片的报告是不可靠的(可能是对的，也可能是错的). 请设计一个算法，使用最少的测试次数来找出 $1$ 片好芯片.

【解】

由于好芯片比坏芯片至少多 $1$ 片，对 $1$ 片芯片来说，如果至少有 $\lfloor \frac{n}{2}\rfloor$ 片芯片到报告它是 “好的”，那么这片芯片一定是好的，否则它就是坏芯片。

最直接的想法就是蛮力法，挨个芯片这般检查，最坏情况下，前 $\lfloor \frac{n}{2}\rfloor$ 片芯片可能都是坏的，最坏情况下的时间复杂度为 $\Theta (n^2)$

要想降低问题的复杂度，初始的想法就是，如何筛选芯片的数量，使比较时的规模减小，从而降低复杂度，这里要考虑 $2$ 个问题：

• 采取什么样的淘汰规则，能够确保下一轮的好芯片比坏芯片至少多 $1$ 片；换句话说，每轮测试丢弃的坏芯片数至少和丢弃的好芯片数一样多
• 每轮测试淘汰的芯片数占测试芯片数的比例是多少，这设计规模减小的有多快，它决定了算法的效率

分析算法一般都是递归算法，子问题一般只是规模减小，但是，其它限定条件一般和原问题一样

先看看不同测试结果报告究竟给出了什么信息：

测试结果

	A报告	B报告	结论
1	B 是好的	A 是好的	A，B都好或都坏
2	B 是好的	A 是坏的	至少一片是坏的
3	B 是坏的	A 是好的	至少一片是坏的
4	B 是坏的	A 是坏的	至少一片是坏的

根据我们要考虑的第一个问题，如果是测试结果 1，那么 A，B 中留 $1$ 片，丢 $1$ 片；如果是后三种情况，则把 A 和 B 全部丢掉

为什么这样可以呢？

当 $n$ 是偶数时，设 A、B 都是好芯片的有 $i$ 组，A、B 一好一坏的有 $j$ 组，A、B 都坏的有 $k$ 组，那么

$$2i+2j+2k=n$$且$$2i+j>2k+j\Rightarrow i>k$$

经过淘汰后，剩下的好芯片数为 $i$，坏芯片数至多为 $k$，满足 $i>k$

但是当 $n$ 是奇数，没被分组而轮空的是 $1$ 片坏芯片时，可能出现淘汰后剩下的好芯片数与坏芯片数相等，对于奇数的情况，可以增加一轮特殊处理，将其按照蛮力法的判断方法，和其他芯片都检测一次，得出芯片的好坏，如果它是好的，算法结束，如果它是坏的，丢弃它.

这些额外的工作需要 $O(n)$ 次测试，而分组内的测试也需要 $O(n)$ 次（精确说是 $\lfloor \frac{n}{2}\rfloor$ 次），因此，不管是奇数还是偶数，规约子问题的工作量都是 $O(N)$

至于第 $2$ 个问题，由于每组至少丢弃掉 $1$ 片芯片，剩下的芯片数至多 $\lfloor \frac{n}{2}\rfloor$

该算法的伪码描述如下：

考虑该算法最坏情况下的时间复杂度，有如下递推方程：

根据前面分析结果，$W(n)=O(n)$，比起蛮力算法，效率有明显提高.

---

【例 2】设 $a$ 是一个给定实数，计算 $a^n$，其中 $n$ 为自然数

【解】

如果使用蛮力算法，算法的时间复杂度是 $O(n)$.

下面考虑分治算法. 将 $a^n$ 看作两部分幂的乘积，每部分都是一个子问题，即 $a^{\frac{n}{2}}$ 幂. 更确切的说，有：

该算法的最坏情况下的时间复杂度有：

$$\begin{array}{rl}W(n)& =W(\frac{n}{2})+O(1)\\ W(1)& =0\end{array}$$

于是得到 $W(n)=O(\log n)$