Fibonacci数列优化以及应用

斐波那契数列是一个非常美丽、和谐的数列，也是一个黄金分割数列。符合黄金分割比0.618。有人说它起源于一对繁殖力惊人、基因非常优秀的兔子，也有人说远古时期的鹦鹉就知道这个规律。
每一个学理工科的学生都知道斐波那契数列，斐波那契数列由如下递推关系式定义：
F(0)=0, F(1)=1, n>1时，F(n)=F(n-1)+F(n-2)。

下面简单地分析一下常见的Fibonacci数列求解算法
1、递归法

int Fibonacci(int n)
{
    if (n <= 0)
        return 0;
    if (n==1 || n==2)
        return 1;
    return Fibonacci(n-1)+Fibonacci(n-2); 
}

递归算法与定义公式十分吻合，容易理解，但计算过程存在大量重复的运算，时间复杂度达到了O(2^n)，使用的内存空间也随着函数调用栈的增长而增长。这显然不适于实用的程序。

2、迭代法

int Fibonacci(int n)
{
    if (n <= 0)
        return 0;
    if (n==1 || n==2)
        return 1;
    int numa=1, numb=1, num;
    for (int i=3; i<=n; ++i)
    {
        num = numa + numb;
        numa = numb;
        numb = num;
    }
    return numb;
}

迭代法的时间复杂度为O(n)，使用的内存空间也不会动态上涨

3、矩阵乘法优化
分两步推导：


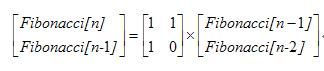
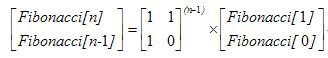
问题的求解就变成矩阵乘法 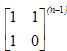求斐波那契数列的解决，而幂的求可用二分法来求。

//Fibonacci矩阵
struct Matrix
{
    long long arr[2][2]; 
};
//基矩阵
Matrix A = 
{
    1, 1,
    1, 0,
};
//单位矩阵
Matrix I = 
{
    1, 0,
    0, 1,
};
//两个矩阵的乘积
Matrix multi(Matrix a, Matrix b)
{
    Matrix ans;
    for (int i=0; i<2; ++i)
    {
        for (int j=0; j<2; ++j)
        {
            ans.arr[i][j] = 0;
            for (int k=0; k<2; ++k)
                ans.arr[i][j] += a.arr[i][k]*b.arr[k][j];
        }
    }
    return ans;
}
//基矩阵的k次方
Matrix power(Matrix m, int k)
{
    Matrix ans = I, tmp=A;
    while (k > 0)
    {
        if (k & 1)
        {
            ans = multi(ans, tmp); 
        }
        k >>= 1;
        tmp = multi(tmp, tmp); 
    }
    return ans;
}

4、进阶问题：1
给出N和K，求Fib(N) mod Fib(K)，由于结果太大，输出Mod 1000000007的结果
1 <= N, K <= 10^18， N<=1000

分析：可以看出本题就是直接求,虽然这里的很大，但是比较小啊，只到1000，那么实际上在Fibonacci数列中有很多有用的性质，比如：

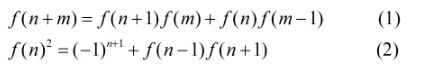
实际上，这个两个公式的推导过程也比较简单。（两种证明方法：带入公式验证；数学归纳法）
所以，我们可以这样来把原表达式变形，即：

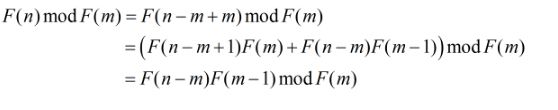
那么，我们继续对用同样的方法对F(n-m)递归下去，容易得到：

可以看出，到了这一步，我们就把所有的Fibonacci数列的下标减小了，基本可以直接计算了。
可以得到
所以到了这里，本题基本就说完了，只需要预处理前1000个Fibonacci数列即可

#include 

using namespace std;

const int N = 1005;
const int MOD = 1000000007;
long long arr[N]; 

//Fibonacci矩阵
struct Matrix
{
    long long arr[2][2]; 
};
Matrix A = 
{
    1, 1,
    1, 0,
};
Matrix I = 
{
    1, 0,
    0, 1,
};

Matrix multi(Matrix a, Matrix b)
{
    Matrix ans;
    for (int i=0; i<2; ++i)
    {
        for (int j=0; j<2; ++j)
        {
            ans.arr[i][j] = 0;
            for (int k=0; k<2; ++k)
            { 
                ans.arr[i][j] += (a.arr[i][k]*b.arr[k][j]) % MOD;
                ans.arr[i][j] %= MOD; 
            }
        }
    }
    return ans;
}

Matrix power(Matrix m, int k)
{
    Matrix ans = I, tmp=A;
    while (k > 0)
    {
        if (k & 1)
        {
            ans = multi(ans, tmp); 
        }
        k >>= 1;
        tmp = multi(tmp, tmp); 
    }
    return ans;
}

int main()
{
    long long n, m;
    cin >> n >> m;
    int numa = n/m;
    int numb = n%m;
    //得到前1000个Fibonacci数列
    for (int i=1; i<=N; ++i)
    {
        arr[i] = power(A, i-1).arr[0][0]; 
        cout << arr[i] << ' '; 
    }

    return 0;
}