「8-Queens Problem」皇后问题局部极值启发式搜索方法
「8-Queens Problem」皇后问题局部极值启发式搜索方法
Backgrounds
背景说明:
皇后问题是算法领域的著名问题,问题的背景是在8*8的国际象棋棋盘上摆满8个皇后使之互相不能攻击(由于皇后在国际象棋规则中横、纵、斜三个方向均可以移动,即摆放要使得皇后两两不在同一横、纵、斜线上)。放松这个问题的变长条件,我们可以将其扩大至N*N的棋盘上摆放N个皇后,使之各自在三个方向上不重复出现。
大一时刚刚学习编程语言的我们,在初次接到这道题时,主要是运用了递归函数和回溯的思想去解决问题,通过深度优先搜索(depth-first search, DFS)策略,依次增加棋盘上可以摆放的位置。若遇到第k步棋子摆放的所有可能位置都发生冲突,则退回到第k-1步,修改k-1的状态,以达到期望的最终解。
State space of 8-queens problem
皇后问题的状态空间:
状态空间,这里理解成所有摆放的可能性情况。
皇后问题广义的解的状态空间,在没有过多限制条件的情况下是非常庞大的。
在64个互不重复的位置上选择无差别的8个位置,总计应该有C(64, 8)=4,426,165,368 (44亿)大小的状态空间. 图示为较为集中的分布情况和可以完全分散开的分布情况。
图 1.1 皇后分布紧凑 图 1.2 皇后分布松散
注意⚠这里C(N*N, N)表示在N*N种方案中选择N个的方案数
不同约束条件下的不同状态空间规模:
实际上,全局解状态空间的大小也由我们的限制条件决定,下面提出两种解决方案。但总体上策略一致地是,我们用一个长度为8的一维数组表示每一列皇后的位置,这种表示方法首先就压缩掉了很大一部分的解的状态空间——因为相当于即使在横向上有皇后可能会重合,这种每列一个位置数的表示方式放弃了同一列上出现多个皇后的情况。图示为横纵均不重合分散分布和允许行重复的分布情况。
图 2.1 允许同行冲突 图 2.2 保证横纵均不冲突
但上述两种表示方法出于求解出尽可能多的局部极值和尽快求解出最优解的考虑,依然是稳妥的。此时状态空间的大小至多已经被压缩至8^8=16,777,216 (1670万)种,相比于44亿已经极大地压缩了解的数量。
(1).第一种表示方法,我们在允许行重合的情况下,每次操作只在该列上对棋子进行上下移动,并考虑每次移动对于总冲突数的影响。
此种排列的状态空间为8^8=16,777,216.
(2).第二种表示方法,我们对1~8的数字进行全排列,得到{a1, a2, …, ai, …, a8}用于表示第i 列上的皇后位置,这样可以保证行列均不重复。
此种排列的状态空间为8!=40,320.
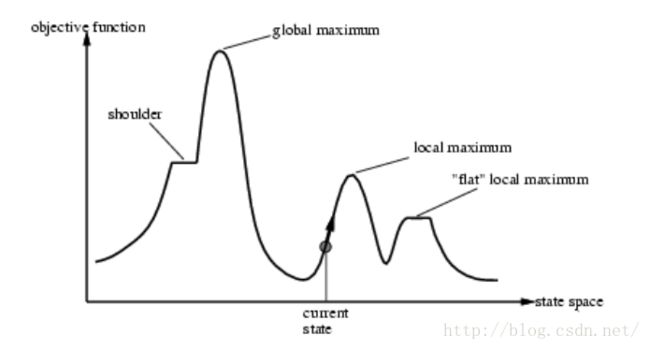
局部极值和全局最值的理解:
全局最值,是对于每一个搜索问题需要找到的最终结果。对于不同的问题,其问题的离散/连续性可能不同,解的数量、状态分布也不相同。皇后问题本身是一个离散问题(解的状态空间数量是有限个数的,虽然解空间总规模可能非常大),且解的数量也是巨大的。至少对于8皇后,不存在唯一的状态。后续运行程序可知,在不考虑翻转、旋转等价的情况下,有92组互不相同的解。即在横纵均不重合的40,320规模的状态空间(或在更大范围的状态空间中)有92组全局最值。
局部极值,是我们通过某种途径趋向全局最值时经过的、不能再用当前算法得出相对更进一步的结果(而必须由重启、重新打乱而继续开始一次新的搜索)时,“卡住”的状态。
图 3 搜索路径与全局最优、局部最优的关系
(state space为构成搜索路径的n维解空间的子集,objective function为目标函数)
对于同一个问题,我们考虑f(x1, x2, …, xi, …, xn)=K的目标函数,希望通过启发式搜索的方式寻找全局K的最优值,即在n维解空间上,我们得到由目标函数f(.)决定的决策-目标曲面。在这个n+1维曲面S(X
其中Ls是某种启发式搜索算法的搜索路径,对于特定的搜索算法,Ls是n维解状态空间的有向路径。记Ls上的每一步解为Xj, 并设该条路径从某一初始状态X0出发,经过p步可以到达全局或局部最优值(其中任意Xj都是n维状态空间上的点),则该路径Ls可以表示为Ls={X0, X1, …, Xj, …, Xp}. 由于状态空间的不平整性,显然通过不同的算法定义到的局部最优解(局部极值)也是不同的。
注意⚠这里的定义包括后续目标函数的定义、估值函数的定义、最终的求解目的等等
Evaluation function
估值函数:
对于启发式搜索,我们需要在巨大的解的状态空间中尽可能快地找出尽可能多的全局最优解,这就需要我们在做每一步选择(选择继续扩大解的已知范围,使之尽快铺展至n维或跳转至下一个解的暂留状态)时,能有效评判该解对于“发现最优解”这一目的的贡献意义的函数。或者我们也可以这样理解:搜索算法在在搜索路径的每一个解Xj停留时,并不知道该解是否处于到达全局最优的必经路径上,因此搜算算法会根据一个估值函数,对“该步操作可以到达全局最优或局部最优”这一事件做出概率分析。当搜索路径Ls走到Xj-1这一步时,会对所有可能的后续状态集合{Xj’|Xj’=Xj’1, Xj’2,…}进行估值,最后选出估值最大的一个Xj’作为Xj下一步。后续也据此方法继续走下去。
当最终走到某一步,估值函数对所有可能的后继都没有最优估值或正向估值时,就说明搜索路径已经到达极值。此时检查目标函数K即可判断当前解是否是全局最优。
需要说明的是,对于全局最优,我们也可以有不同的定义方法。在本问题中,我们选择用“冲突行、列或斜线上棋子数减一”表示冲突情况,即当某行、列或斜线上皇后棋子数目为0个或1个时,认为没有冲突;皇后棋子数目为2个及以上时,认为冲突数是皇后数目-1.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
int
getChange(
int
i,
int
j) {
int
pi = position[i], pj = position[j];
// i-pi, j-pj
// left: i+pi==j+pj, right: i-pi==j-pj
// left[i+pi-1] left[j+pj-1] right[N-(i-pi)] right[N-(j-pj)]
if
(i+pi == j+pj) {
// same left line
return
((left[i+pi-1]>=3)+1)
+ (right[N-(i-pi)]>=2)
+ (right[N-(j-pj)]>=2)
- ((right[N-(i-pj)]>=1)+1)
- (left[i+pj-1]>=1)
- (left[j+pi-1]>=1);
}
else
if
(i-pi == j-pj) {
// same right line
return
((right[N-(i-pi)]>=3)+1)
+ (left[i+pi-1]>=2)
+ (left[j+pj-1]>=2)
- ((left[i+pj-1]>=1)+1)
- (right[N-(i-pj)]>=1)
- (right[N-(j-pi)]>=1);
}
else
{
// (i, j) no collision
return
(left[i+pi-1]>=2)
+ (left[j+pj-1]>=2)
+ (right[N-(i-pi)]>=2)
+ (right[N-(j-pj)]>=2)
- (left[i+pj-1]>=1)
- (left[j+pi-1]>=1)
- (right[N-(i-pj)]>=1)
- (right[N-(j-pi)]>=1);
}
}
|
图 4 估值函数
当发现两列(i, j) 可以被操作时,我们通过计算“交换后”与“交换前”两种状态(两个不同的解的停留点)之间目标函数即总冲突数的变化量,判断该步操作是否应被执行。其中我们考虑了交换前的(i, j)两列处于左斜向冲突(交换后存在右斜向冲突)、右斜向冲突(交换后存在左斜向冲突)、无冲突(交换后彼此依然无冲突)三种情况。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
void
statistic() {
clear();
for
(
int
i=1; i<=N; ++i) {
int
pi=position[i];
left[i+pi-1]++;
right[N-(i-pi)]++;
}
}
void
reCount() {
statistic();
Collision = 0;
leftCollision = 0, rightCollision = 0;
for
(
int
i=1; i<=2*N-1; ++i) {
if
(left[i]>=2) leftCollision += left[i]-1;
if
(right[i]>=2) rightCollision += right[i]-1;
}
Collision = leftCollision + rightCollision;
}
|
图 5 目标函数定义,显然Collision=0时取得全局最优解
Main Algorithm
状态空间压缩:
我们选择交换不重复的列来完成全局最优的搜索结果,这样可以在本身就比较小的状态空间(40,320种)范围内得出结果。并且对于全局最优来说,由于所有的全局最优解均包含在该状态空间中,全局最优的分布率也最高。
重启策略:
初始化时生成1到8的升序列并进行时间复杂度O(n)的遍历,每次随机出一个位置,将其与当前扫到的位置做一次交换。之后每次重启仅对现有列进行一次随机交换即可得到一个新的解空间上的X0作为新的一条搜索路径Ls的起点。
搜索策略:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public
:
void
solve(
bool
ptl) {
bool
moveOn =
true
;
int
EFT = 0;
rebootCount = 0;
reCount();
// initialization process
startCTime =
clock
();
while
(!finish()) {
// Terminate
reboot();
rebootCount++;
reCount();
EFT=0; moveOn=
true
;
while
(moveOn) {
moveOn =
false
;
for
(
int
i=1; i<=N; ++i) {
for
(
int
j=1; j
// -------------beginforeach i, j
EFT = 0;
// for any 'i' col & 'j' col
if
(collapsed(i, j)) {
// (i, j) pair collapsed
EFT = getChange(i, j);
}
else
EFT = -1;
if
(EFT>0) {
// still trends to minimal
moveOn =
true
;
// do position swapping
// maintain the array 'left' & 'right'
execSwap(i, j);
}
reCount();
// -------------------------- endforeach i, j
}
}
}
if
(ptl) {
puff();
prinf();
}
}
endCTime =
clock
();
costCTime = endCTime - startCTime;
}
|
图 6 主要搜索方法
用两个主要变量控制搜索进程:
int EFT用来衡量每次可交换列的对(i, j)交换后的估值函数值;
bool moveOn判断当前循环是否有效,即是否有正向估值产生。
每当一步搜索不能产生正向估值,即无论如何移动也不能使总的冲突数减小时,一个新的局部极值就可能被找到了。这时我们若判断出总冲突数降至0则可以进一步说明这个极值也是一个全局最优。
Local search strategy
贪心与模拟退火:
爬山问题中,我们判断当前搜索方向是否还会继续趋向于更大值。若当前搜索方向上不再出现上升态势,搜索会停止并驻留在当前解上(即局部最优解),所以爬山策略是一种严格贪心算法,不保证可以找到全局最优。
模拟退火算法正是通过增加一定几率的反向跳转趋势,使得搜索位置得以“逃脱”局部最优,获得移动到全局最优的可能;通过控制反向跳转几率的收敛,使得解有更大可能性最终停留在全局最优解上。
局部搜索策略:
皇后问题中,局部最优解的分布较为稠密,全局最优解的比例也相对较高。这使得模拟退火等一般意义上的概率收敛不一定能取得较好的效果。
Simple Statistic
简单统计结果:
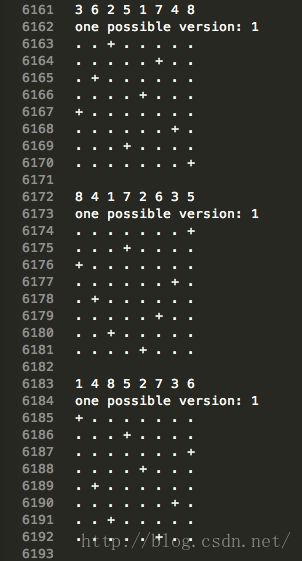
下面给一个运行的例子
50000次运行求出最优解,平均每个最优解的求得只需要2.6次重启,即经过2.6个局部最优解到达了全局最优;启动最多的也只有25次;平均耗时极短。
程序打印出的一些局部极值示意图
ps. 最近新开通了博客 会放一些学习过程中的心得体会(和一些作业或者报告)
如果你觉得有用,欢迎分享,谢谢!