关于《剑指offer》的66道编程题的总结(六)
2019年9月9日16:37:41
文章目录
- (第五十一题)矩形覆盖
- (第五十二题)树的子结构
- (第五十三题)顺时针打印矩阵
- (第五十四题)删除链表中重复的节点
- (第五十五题)连续子数组的最大和
- (第五十六题)链表中环的入口结点
- (第五十七题)剪绳子
- (第五十八题)机器人的运动范围
- (第五十九题)数据流中的中位数
- (第六十题)滑动窗口的最大值
(第五十一题)矩形覆盖
2019年9月9日16:43:33
题目链接:
https://www.nowcoder.com/practice/72a5a919508a4251859fb2cfb987a0e6?tpId=13&tqId=11163&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:原理和斐波那契数列一样
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月9日16:40:13
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间: 2019年9月9日16:44:19
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include (2) n等于2时,总共有2种方法。
2*1的矩形,横着或竖着分别一种。
(3) n等于3时,总共有3种方法。
- 2 * 1的矩形全部竖着放;
2)第一列 21的矩形竖着放,后面两列横着放两个21的矩形;
3)前面两行横着放两个21的矩形,最后一列竖着放一个21的矩形。
我们可以看到,由于21的小矩形可以横着放也可以竖着放,当n=3的时候,在n=2的基础上其实只有一种放法了,就是把第三个21的小矩形竖着放,在n=1的基础上,把第二个和第三个2*1的小矩形横着放(有人会说为什么竖着放两个不算,这已经包括在n=2的情况下了)。所以抽象表示就是f(3)=f(2)+f(1)。
类似于 斐波那契数列。注:做题的时候,不要慌 认真分析一下,列举几个数据 总结规律。这考的不是代码能力,而是数学分析总结能力。
(第五十二题)树的子结构
2019年9月9日17:20:57
题目链接:
https://www.nowcoder.com/practice/6e196c44c7004d15b1610b9afca8bd88?tpId=13&tqId=11170&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月9日16:44:19
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间: 2019年9月9日17:21:13
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include (第五十三题)顺时针打印矩阵
2019年9月9日18:54:54
题目链接:
https://www.nowcoder.com/practice/9b4c81a02cd34f76be2659fa0d54342a?tpId=13&tqId=11172&tPage=1&rp=1&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月9日18:19:04
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间:2019年9月9日18:54:12
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include (第五十四题)删除链表中重复的节点
2019年9月9日20:26:51
题目链接:
https://www.nowcoder.com/practice/fc533c45b73a41b0b44ccba763f866ef?tpId=13&tqId=11209&tPage=3&rp=3&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月9日19:02:07
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间: 2019年9月9日20:18:19
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include (第五十五题)连续子数组的最大和
2019年9月9日20:58:47
题目链接:
https://www.nowcoder.com/practice/459bd355da1549fa8a49e350bf3df484?tpId=13&tqId=11183&tPage=2&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月9日20:33:23
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间: 2019年9月9日20:59:40
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include (第五十六题)链表中环的入口结点
2019年9月10日12:31:51
题目链接:
https://www.nowcoder.com/practice/253d2c59ec3e4bc68da16833f79a38e4?tpId=13&tqId=11208&tPage=3&rp=3&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
/**══════════════════════════════════╗
*作 者:songjinzhou ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub:https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
*═══════════════════════════════════╣
*创建时间:2019年9月10日11:04:43
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间: 2019年9月10日11:29:45
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include
#include
#include 
分析如下:
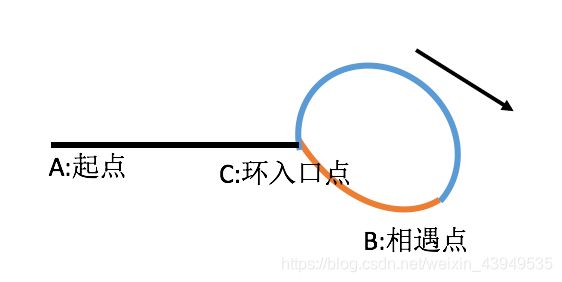
假设x为环前面的路程(黑色路程),a为环入口到相遇点的路程(蓝色路程,假设顺时针走), c为环的长度(蓝色+橙色路程)
当快慢指针相遇的时候:
此时慢指针走的路程为Sslow = x + m * c + a
快指针走的路程为Sfast = x + n * c + a
2 Sslow = Sfast
2 * ( x + m * c + a ) = (x + n * c + a)
从而可以推导出:
x = (n - 2 * m ) * c - a
= (n - 2 * m -1 ) * c + c - a
即环前面的路程 = 数个环的长度(为可能为0) + c - a
什么是c - a?这是相遇点后,环后面部分的路程。(橙色路程)
所以,我们可以让一个指针从起点A开始走,让一个指针从相遇点B开始继续往后走,
2个指针速度一样,那么,当从原点的指针走到环入口点的时候(此时刚好走了x)
从相遇点开始走的那个指针也一定刚好到达环入口点。
所以2者会相遇,且恰好相遇在环的入口点。
最后,判断是否有环,且找环的算法复杂度为:
时间复杂度:O(n)
空间复杂度:O(1)

2019年9月10日14:08:08
(第五十七题)剪绳子
2019年9月10日15:28:38
题目链接:
https://www.nowcoder.com/practice/57d85990ba5b440ab888fc72b0751bf8?tpId=13&tqId=33257&tPage=4&rp=4&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:

方法1:数学归纳,最好的方法。但是不做重点,因为我们是在学习。
代码如下:
/**
* 题目分析:
* 先举几个例子,可以看出规律来。
* 4 : 2*2
* 5 : 2*3
* 6 : 3*3
* 7 : 2*2*3 或者4*3
* 8 : 2*3*3
* 9 : 3*3*3
* 10:2*2*3*3 或者4*3*3
* 11:2*3*3*3
* 12:3*3*3*3
* 13:2*2*3*3*3 或者4*3*3*3
*
* 下面是分析:
* 首先判断k[0]到k[m]可能有哪些数字,实际上只可能是2或者3。
* 当然也可能有4,但是4=2*2,我们就简单些不考虑了。
* 5<2*3,6<3*3,比6更大的数字我们就更不用考虑了,肯定要继续分。
* 其次看2和3的数量,2的数量肯定小于3个,为什么呢?
6=2+2+2 6=3+3
因为2*2*2<3*3,那么题目就简单了。
* 直接用n除以3,根据得到的余数判断是一个2还是两个2还是没有2就行了。
* 由于题目规定m>1,所以2只能是1*1,3只能是2*1,这两个特殊情况直接返回就行了。
*
* n % 3只能有0 1 2三种情况
* 0则全分成3
* 1的话:比如13 可以分成3 3 3 3 1,则为81 ;而后面的3+1=4 可以分成2 * 2 =4 > 3
* 2的话:比如14、8等可以分成3 3 3 3 2,直接相乘即可
*
* 乘方运算的复杂度为:O(log n),用DP来做会耗时比较多。
*/
class Solution {
public:
int cutRope(int number)
{
if (number <= 1)
return 0;
if (number == 2 || number == 3)
return number - 1;
int save_of_3 = number % 3;//n的余数
int numb_of_3 = number / 3;//最多可以分出来几个3
if (save_of_3 == 0)
{
return pow(3, numb_of_3);//全分成3
}
else if (save_of_3 == 1)
{
return pow(3, numb_of_3 - 1) * 2 * 2;//最后留出一个4 变成2*2
}
else
{
return pow(3, numb_of_3) * 2;//留下的2 乘上即可
}
}
};
int main()
{
Solution solution;
cout << solution.cutRope(8) << endl;
return 0;
}
方法2:贪心算法:尽量剪出长度3,若最后剩长度4,就剪2 * 2
当n大于等于5时,我们尽可能多的剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。 为什么选2,3为最小的子问题?因为2,3包含于各个问题中,如果再往下剪得话,乘积就会变小。 为什么选长度为3?因为当n≥5时,3(n−3)≥2(n−2)。
代码如下:
class Solution {
public:
int cutRope(int number)
{
if (number <= 1)
return 0;
if (number == 2 || number == 3)
return number - 1;
int save_of_3 = number % 3;//n的余数
int numb_of_3 = number / 3;//最多可以分出来几个3
//贪心算法:
//余数是1的话:比如13 可以分成3 3 3 3 1,则为81 ;
//而后面的3+1=4 可以分成2 * 2 =4 > 3
if (save_of_3 == 1)
numb_of_3--;//最多可以分出来的 拿出来给2分
//最多可以分出来几个2
int numb_of_2 = (number - 3 * numb_of_3) / 2;
return pow(3, numb_of_3) * pow(2, numb_of_2);
}
};
方法3:DP
动态规划求解问题的四个特征:
①求一个问题的最优解;
②整体的问题的最优解是依赖于各个子问题的最优解;
③小问题之间还有相互重叠的更小的子问题;
④从上往下分析问题,从下往上求解问题;
动态规划:长度为i的可得最大乘积:dp[i]=dp[j]*dp[i-j]的最大值。动态规划:最大成绩,有点类似于完全背包问题。
class Solution {
public:
int cutRope(int number)
{
if (number <= 1)
return 0;
if (number == 2 || number == 3)
return number - 1;
vector<int>myvec_dp;
myvec_dp.push_back(0);
myvec_dp.push_back(1);
myvec_dp.push_back(2);
myvec_dp.push_back(3);
//动态规划:长度为i的可得最大乘积:dp[i]=dp[j]*dp[i-j]的最大值
for (int i = 4; i <= number; ++i)//i从4开始
{
int maxlen = 0;
for (int j = 2; j <= i/2; ++j)
{
if (myvec_dp[j] * myvec_dp[i - j] > maxlen)
maxlen = myvec_dp[j] * myvec_dp[i - j];
}
myvec_dp.push_back(maxlen);//这就是dp[i]的值
}
return myvec_dp[number];
}
};
(第五十八题)机器人的运动范围
2019年9月10日18:17:40
题目链接:
https://www.nowcoder.com/practice/6e5207314b5241fb83f2329e89fdecc8?tpId=13&tqId=11219&tPage=4&rp=4&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
class Solution {
public:
int getNum(int number)
{
if (number < 10)
return number;
else
{
int result = 0;
while (number != 0)
{
result += number % 10;
number /= 10;
}
return result;
}
}
int moving_Operator(int threshold, int rows, int cols,int i,int j, bool* isVisited)
{
int num = 0;
if (0 <= i && i < rows && 0 <= j && j < cols && !isVisited[i * cols + j]
&& (getNum(i) + getNum(j) <= threshold))
{
isVisited[i * cols + j] = 1;//没有被访问过 且 满足条件
num++;
num += moving_Operator(threshold, rows, cols, i, j + 1, isVisited);
num += moving_Operator(threshold, rows, cols, i - 1, j, isVisited);
num += moving_Operator(threshold, rows, cols, i + 1, j, isVisited);
num += moving_Operator(threshold, rows, cols, i, j - 1, isVisited);
}
return num;
}
int movingCount(int threshold, int rows, int cols)
{
if (rows <= 0 || cols <= 0 || threshold <= 0)
return 0;
//m行n列
//假如说 从左下角开始(0,0)一直到右上角(m-1,n-1)
bool* isVisited = new bool[rows * cols];
memset(isVisited, 0, cols * rows);
int totalnum = moving_Operator(threshold, rows, cols, 0, 0, isVisited);
delete[]isVisited;
return totalnum;
}
};
2019年9月10日18:19:04
(第五十九题)数据流中的中位数
2019年9月10日19:47:25
题目链接:
https://www.nowcoder.com/practice/9be0172896bd43948f8a32fb954e1be1?tpId=13&tqId=11216&tPage=4&rp=4&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
class Solution {
public:
void Insert(int num)
{
myvec.push_back(num);
sort(myvec.begin(), myvec.end());
}
double GetMedian()
{
int size = myvec.size();
if (size % 2 == 1)
{
return (double)myvec[size / 2];
}
else
{
double val1 = (double)myvec[size / 2 - 1];
double val2 = (double)myvec[size / 2];
return (val1 + val2) / 2;
}
}
private:
vector<int>myvec;
};
2019年9月10日20:24:21
(第六十题)滑动窗口的最大值
2019年9月10日20:24:56
题目链接:
https://www.nowcoder.com/practice/1624bc35a45c42c0bc17d17fa0cba788?tpId=13&tqId=11217&tPage=4&rp=4&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking
题目描述:
代码如下:
class Solution {
public:
vector<int> maxInWindows(const vector<int>& num, unsigned int size)
{
vector<int>myvec;
if (size == 0 || num.size() == 0 || size > num.size())
return myvec;
int len = num.size();
//if (size >= len)
//{
// int maxval = num[0];
// for (int val : num)
// {
// if (val > maxval)
// maxval = val;
// }
// myvec.push_back(maxval);
//}
for (int i = 0; i <= len-size; ++i)
{
vector<int>temp_vec;
for (int j = 0; j < size; ++j)
{
temp_vec.push_back(num[j + i]);
}
sort(temp_vec.begin(), temp_vec.end());
myvec.push_back(temp_vec[size - 1]);
}
return myvec;
}
};
2019年9月10日20:25:54