Matrix的用法详解

稀释矩阵顾名思义是非零值分布较少的矩阵，处理稀释矩阵一般用到三个包，Matrix,slam and glmnet包，前两个用于存储与处理稀释矩阵，后者是用于稀释矩阵的广义线性模型的分析。

Matrix 包

Doug Bates 的Matrix包能够非常方便地将矩阵在全矩阵和稀释矩阵间转换

举个例子，用系统自带的matrix函数生成1000*1000的数值为零的矩阵，和用Matrix函数生成同样的矩阵，如下所示：

1 2 3 4 5 6 7 8 9

library('Matrix')   m1 <- matrix(0, nrow =1000, ncol =1000) m2 <- Matrix(0, nrow =1000, ncol =1000, sparse = TRUE)   object.size(m1) # 8000200 bytes object.size(m2) # 5632 bytes

你能看到，matrix生成的矩阵占有的内存（RAM）比Matrix高1500倍以上，但是假如两个矩阵用的是非零矩阵，效果会如何呢？

1 2 3 4 5 6 7

m1[500,500]<-1 m2[500,500]<-1   object.size(m1) # 8000200 bytes object.size(m2) # 5648 bytes

全矩阵并未改变内存值，因为所有零值一开始就已经被展示出来了，而稀释矩阵在非零值增加后，其内存值就发生了改变。测试发现，稀释矩阵增加一个非零值，其内存增加16BYTES，因此将所有零值替换为非零值，稀释矩阵将增加5632+16*1000*1000BYTES，即16005632BYTES，差不多是用matrix函数创建的矩阵所占内存的两倍。

因此，假如你的矩阵是稀释的，那么用Matrix会相当高效，而非稀释的话，则相对低效。

除了初始化和指定任务作业上，我们也能用Matrix包做很多其它操作，如向量相乘、相加、相减和转换：

1 2 3 4

m2 %*% rnorm(1000) m2 + m2 m2 - m2 t(m2)

同时，也能用cBind和rBind进行合并工作；

1 2 3 4 5 6 7

m3 <- cBind(m2, m2) nrow(m3) ncol(m3)   m4 <- rBind(m2, m2) nrow(m4) ncol(m4)

slam 包

Slam包是由Kurt Hornik设计的，使用这个包生成的稀释矩阵远比用Matrix包要小的多。

比如，生成一个上述第一个这样的稀释矩阵只要1032BYTES：

1 2 3 4 5 6 7 8 9

library('slam')   m1 <- matrix(0, nrow =1000, ncol =1000) m2 <- simple_triplet_zero_matrix(nrow =1000, ncol =1000)   object.size(m1) # 8000200 bytes object.size(m2) # 1032 bytes

当然，我们也要看看每增加一个非零值，内存增量是多少（结果可以自己运算比较一下）：

1 2 3 4 5 6

m1[500,500]<-1 m2[500,500]<-1   object.size(m1) object.size(m2)

最后，所有对矩阵的运算方式和Matrix一样：

1 2 3 4

m2 %*% rnorm(1000) m2 + m2 m2 - m2 t(m2)

glmnet 包

当然，以上所有处理的目的是用于最终分析的，不然就无降低内存的意义；GLM是分析该数据的一种通用性较广的方法，多数时候用线性和逻辑回归就足以，当然需要加上部分规则以优化模型。

Glmnet包可被用于处理稀释矩阵而无需转换成如数据框的形式：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

library('Matrix') library('glmnet')   n <-10000 p <-500   x <- matrix(rnorm(n * p), n, p) iz <- sample(1:(n * p),              size = n * p *0.85,              replace = FALSE) x[iz]<-0   object.size(x)   sx <- Matrix(x, sparse = TRUE)   object.size(sx)   beta <- rnorm(p)   y <- x %*% beta + rnorm(n)   glmnet.fit<- glmnet(x, y)

使用稀释矩阵有多高效？下面用GLMNET包对稀释矩阵和全矩阵的处理速度作了对比

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

library('Matrix') library('glmnet')   set.seed(1) performance <- data.frame()   for(sim in 1:10) {    n <-10000    p <-500      nzc <- trunc(p /10)      x <- matrix(rnorm(n * p), n, p)    iz <- sample(1:(n * p),                size = n * p *0.85,                replace = FALSE)    x[iz]<-0    sx <- Matrix(x, sparse = TRUE)      beta <- rnorm(nzc)    fx <- x[, seq(nzc)]%*% beta      eps <- rnorm(n)    y <- fx + eps      sparse.times<- system.time(fit1 <- glmnet(sx, y))    full.times<- system.time(fit2 <- glmnet(x, y))    sparse.size<- as.numeric(object.size(sx))    full.size<- as.numeric(object.size(x))      performance <- rbind(performance, data.frame(Format ='Sparse',                                                UserTime = sparse.times[1],                                                 SystemTime = sparse.times[2],                                                 ElapsedTime = sparse.times[3],                                                 Size = sparse.size))    performance <- rbind(performance, data.frame(Format ='Full',                                                 UserTime = full.times[1],                                                 SystemTime = full.times[2],                                                ElapsedTime = full.times[3],                                                 Size = full.size)) }   ggplot(performance, aes(x = Format, y = UserTime, fill = Format))+    stat_summary(fun.data='mean_cl_boot', geom ='bar')+    stat_summary(fun.data='mean_cl_boot', geom ='errorbar')+    ylab('User Time in Seconds')+    opts(legend.position='none') ggsave('sparse_vs_full_user_time.pdf')   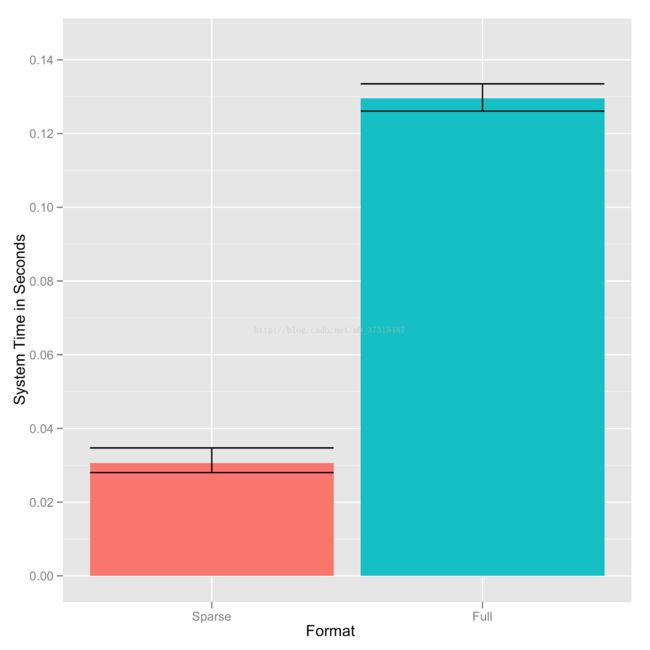ggplot(performance, aes(x = Format, y = SystemTime, fill = Format))+    stat_summary(fun.data='mean_cl_boot', geom ='bar')+    stat_summary(fun.data='mean_cl_boot', geom ='errorbar')+    ylab('System Time in Seconds')+    opts(legend.position='none') ggsave('sparse_vs_full_system_time.pdf')   ggplot(performance, aes(x = Format, y = ElapsedTime, fill = Format))+    stat_summary(fun.data='mean_cl_boot', geom ='bar')+    stat_summary(fun.data='mean_cl_boot', geom ='errorbar')+    ylab('Elapsed Time in Seconds')+    opts(legend.position='none') ggsave('sparse_vs_full_elapsed_time.pdf')   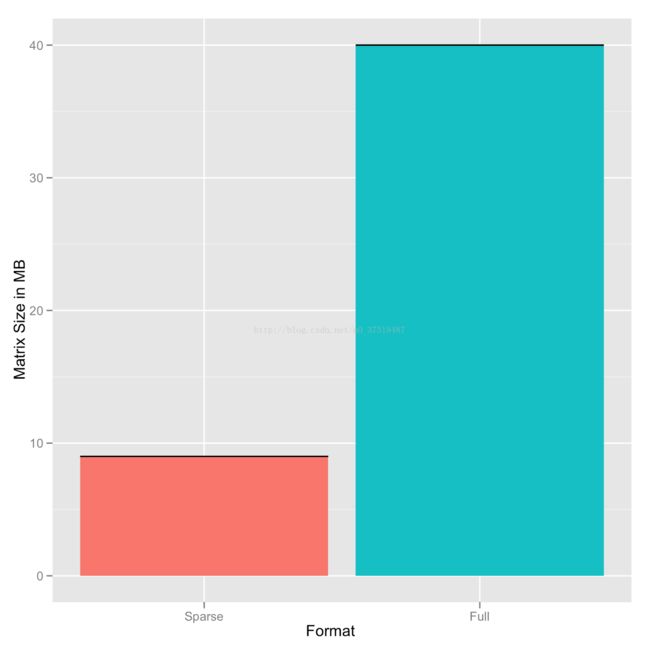ggplot(performance, aes(x = Format, y = Size /1000000, fill = Format))+    stat_summary(fun.data='mean_cl_boot', geom ='bar')+    stat_summary(fun.data='mean_cl_boot', geom ='errorbar')+    ylab('Matrix Size in MB')+    opts(legend.position='none') ggsave('sparse_vs_full_memory.pdf')

以下是结果图:

########################################################################

欢迎微信交流：左码为作者微信，右码为作者公众号（博客文章会同步于公众号发布）