线段树进阶学习(例题)--树状数组学习+离散化+成端更新+区间合并+扫描线
树状数组
一、树状数组简介
树状数组(Binary Indexed Trees,简称BIT)是一种特殊的数据结构,这种数据结构的时空复杂度和线段树相似,但是它的系数要小得多。它可以方便地查询出一段区间中的数字之和。其查询和修改的时间复杂度均为O(lbN),并且是一个在线的数据结构,可以随时修改并查询。我接下来用一道题目来介绍树状数组的几个基本操作。
【引例】
假设有一列数{Ai}(1<=i<=n),支持如下两种操作:
1. 将Ak的值加D。(k,D是输入的数)
2. 输出 (s,t都是输入的数,s<=t)
这道题目用线段树很容易可以解决,我就不多说了,那么如何用树状数组来解决呢?我们新增一个数组C[],其中C[i]=a[i-2k+1]+……+a[i] (k为i在二进制形式下末尾0的个数)。根据定义我们可以得出一下这张表格:
i 二进制 K
1 (1)2 0 c[1]=a[1]
2 (10) 2 1 c[2]=a[1]+a[2]=c[1]+a[2]
3 (11) 2 0 c[3]=a[3]
4 (100) 2 2 c[4]=a[1]+a[2]+a[3]+a[4]=c[2]+c[3]+a[4]
5 (101) 2 0 c[5]=a[5]
6 (110) 2 1 c[6]=a[5]+a[6]=c[5]+a[6]
……
在这里,我们会发现k值的求解会有一些难度,这就引出了树状数组的第一个操作:低位技术,也叫Lowbit(k)。
对于Lowbit这里我提三种不同的写法(这三种形式是等价的,读者有兴趣可以去证明一下):
1.Lowbit(k)=k and (k or (k-1))
2.Lowbit(k)=k and not (k-1)
3.Lowbit(x)=k and –k
然后我来分析引例的树状数组解法,为了可以更好地理解这种方法,读者可以根据以下这幅图来加以理解。
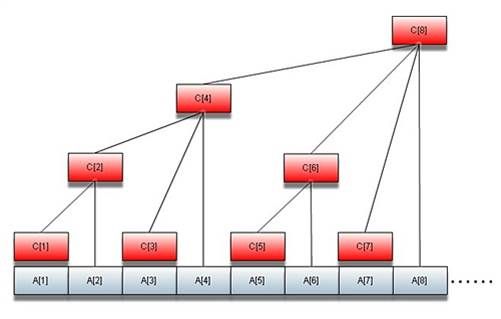
两个基本操作
void add(int k,int d)
{
while(kint sum(int k)
{
int ret=0;
while(k>0)
{
ret+=arr[k];
k-=k&-k;
}
return ret;
} 模式一:更改某些位上的数值,比如第i个数+k,-k等。
模式二:更改一个区间
在这种模式下,a[i]已经不再表示真实的值了,只不过是一个没有意义的、用来辅助的数组。这时我们真正需要的是另一个假想的数组b[],b[i] 才表示真实的元素值。但 c[] 数组却始终是为a[]数组服务的,这一点大家要明确。此时Sum(i)虽然也是求a[i]之前的元素和,但它现在表示的是实际我要的值,也就是 b[i]。
比如现在我要对图1 中a[]数组中红色区域的值全部1。当然你可以用模式一的 Modify(i)对该区间内的每一个元素都修改一次,但如果这个区间很大,那么每次修改的复杂度就都是O(NlbN),m次修改就是O(MNlbN),这在M和N很大的时候仍是不满足要求的。这时模式二便派上了用场。我只要将该区域的第一个元素+1,最后一个元素的下一位置-1,对每个位置Sum(i)以后的值见图2:
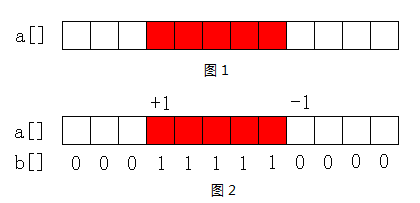
例题poj2481
题意就是求出每个区间被真子覆盖(即被覆盖,但区间不一样)的次数。
将每个区间按Ri从大到小进行排序,若Ri相等,按Li从小到大排序。
为什么,这样排保证从0~n-1每次加入的区间一定不会被后面的覆盖,换句话说加进来后就可以立刻求出覆盖(注意这里是覆盖,不是真子覆盖)他的区间数。每次加进一个区间,那么整个区间[i,j]要加1,用树状数组的话只需i的位置+1;j+1的位置-1。而计算覆盖他的区间数就等于区间左端点位置上的数(即sum(i))。
由于是真子覆盖,所以要去掉区间相等,不多解释,看代码吧-。-
#include scanf("%d %d",&cow[i].s,&cow[i].e);
cow[i].id=i;
cow[i].s++,cow[i].e++;
kn=max(kn,cow[i].e);
}
qsort(cow,n,sizeof(struct _cow),mcmp);
int cnt=1;
for(int i=1;iif(cow[i].e==cow[i-1].e&&cow[i].s==cow[i-1].s)
{ans[cow[i].id]-=cnt;cnt++;}
else cnt=1;
}
for(int i=0;i1);
add(cow[i].e+1,-1);
}
for(int i=0;iprintf("%d%c",ans[i],i==n-1?'\n':' ' );
}
return 0;
} 例题poj1990
题意: 奶牛节:N头奶牛每头耳背程度v,坐标x。两牛交流需要音量为distance * max(v(i),v(j)),求所有牛两两交流所需总和?
刚接触树状数组,完全没想到用两个树状数组来做这道题,看别人题解也是看了半天才明白。。。。药丸
将牛按照耳背程度升序后,一头一头地加入奶牛节。这样是为了保证加入每一头的时候,这头牛的耳背程度肯定是最大的,那么就用这头牛的耳背程度乘以这头牛到当前所有牛的距离即可。
所以问题就转化为求这头牛到当前所有牛的距离。
假设这头牛当前位置为x,它左边有l头牛,右边有r头牛;
∑|x-pi|=∑(x-l _pi)+∑(r _pi-x)=l*x-∑l _pi+∑r _pi-r *x;
这题用到了两个BIT,分别是个数BIT和距离BIT。这样就可以用个数bit求出l和r,用距离BIT求出l _pi和r _pi。(看了别人代码才懂,。。。。。)
#include scanf("%d %d",&cow[i].v,&cow[i].pos);
qsort(cow,n,sizeof(struct _cow),cmp);
ms(cnt_bit);
ms(dis_bit);
LL res=0;
for(int i=0;iint tv=cow[i].v,x=cow[i].pos;
int l=sum(cnt_bit,1,x),r=sum(cnt_bit,x+1,20010);
res+=(LL)tv*(l*x-sum(dis_bit,1,x)+sum(dis_bit,x+1,20010)-r*x);
add(cnt_bit,x,1);
add(dis_bit,x,x);
}
printf("%lld\n",res );
return 0;
} 例题poj2155
二维树状数组
做这道题类比一维数组的区间更新,更新[i,j]是将i的位置+1,将j+1的位置-1.所以二维应该是将(a,b)的位置+1,(a,c+1)的位置-1,(d+1,b)的位置-1,再将(c+1,d+1)的位置+1.(更新的是矩形(a,b)—(c,d))
完全可以扩展到三维将(a,b,c)的位置+1,(a,b,f+1)的位置-1,(a,e+1,c)的位置-1,再将(d+1,b,c)的位置-1,(a,e+1,f+1)的位置+1,(d+1,e+1,c)的位置+1,再将(d+1,b,f+1)的位置+1,再将(d+1,e+1,f+1)的位置-1。(更新的是长方体(a,b,c)—(d,e,f)))
容斥原理23333
#include 离散化
就是简单哈希,例如把154 456 6767映成1 2 3,当然一半要保证能映回去。以下这道例题非常经典,计算离散化错了也能水过去。
比如1-4 5-10和
1-4 6-10一般离散化后都是1-2 3-4,
所以如果两个数字之间的差大于一就应该在他们中间加一个数
比如 51 74 108 109 391
应该先变为51 73 74 107 108 109 390 391 。
这样子就应该能理解。
这道题要用到成段更新(lazy标记),简而言之就是每次更新不更新到底。怎么做到呢?使用一个标记它更新了,等到要访问它儿子时才更新它的儿子,然后lazy标记就传给它的儿子。
例题POJ2528 Mayor’s posters
#include int mid=l+((r-l)>>1);
if(hash[mid]1;
else if(hash[mid]>num) r=mid;
else return mid;
}
return -1;
}
void pushdown(int tn)
{
if(lazy[tn]){
lazy[tn<<1]=lazy[tn<<1|1]=lazy[tn];
lazy[tn]=0;
}
}
void chang(int tn,int l,int r,int c,int x,int y)
{
if(x<=l&&r<=y) {lazy[tn]=c;return;}
pushdown(tn);
int mid=l+((r-l)>>1);
if(x<=mid) chang(tn<<1,l,mid,c,x,y);
if(y>mid) chang(tn<<1|1,mid+1,r,c,x,y);
}
void query(int tn,int l,int r)
{
if(lazy[tn]) {
if(!iscv[lazy[tn]]) cnt++;
iscv[lazy[tn]]=true;
return;}
if(l>=r) return;
int mid=l+((r-l)>>1);
query(tn<<1,l,mid);
query(tn<<1|1,mid+1,r);
}
int main(int argc, char const *argv[])
{
int c;
cin>>c;
while(c--)
{
int n;
scanf("%d",&n);
int mmm=0;
for(int i=0;iscanf("%d %d",li+i,ri+i);
hash[mmm++]=li[i];
hash[mmm++]=ri[i];
}
sort(hash,hash+mmm);
m=1;
for(int i=1;iif(hash[i]!=hash[i-1]) hash[m++]=hash[i];
for(int i=m-1;i>0;i--)
if(hash[i]!=hash[i-1]+1) hash[m++]=hash[i-1]+1;
sort(hash,hash+m);
ms(lazy);
for(int i=0;iint l=find(li[i]),r=find(ri[i]);
chang(1,0,m-1,i+1,l,r);
}
ms(iscv);
cnt=0;
query(1,0,m-1);
printf("%d\n",cnt);
}
return 0;
} 成段更新
例题poj3225 HELP WITH INTERVALS
用0和1表示区间的覆盖情况,-1表示延迟标记已经下移,同时也表示这个区间是被部分覆盖
对于[a,b],用奇数来代表开区间,偶数来代表闭区间
比如(a,b),就应该转化为[2 *a+1,2 *b-1]
(a,b], [ 2 *a+1, 2 *b]
[a,b), [ 2 *a, 2 *b-1]
对于每一个操作,
U [i, j], [i,j]=1
I [i,j] (-oo,i-1] U [j+1,+oo]=0
D [i,j] [i,j] =0
C [i,j] (-oo,i-1] U [j+1,+oo]=0并且[i,j]对1异或
S [i,j] [i,j]对1异或
难点在于区间对1异或
如果一个区间被覆盖后,异或标记应该被销毁。
当一个节点得到异或标记时,应该先判断覆盖标记,如果是0或1,直接改变覆盖标记,否则改异或标记。
最后扫一遍,把所有坐标上的点的状态记录起来。
#include if(myhash[i]){
if(s==-1) s=i;
t=i;
}
else if(s!=-1){
if(flg) putchar(' ');
flg=true;
printf("%c%d,%d%c",(s&1)?'(':'[',
s>>1,(t+1)>>1,(t&1)?')':']' );
s=-1;
}
if(flg) putchar('\n');
else puts("empty set");
return 0;
} 区间合并
区间合并难点就是在push_up函数,也是看了很久才懂。
例题hdu3308 LCIS
两个难点: 向上更新和查找
向上更新(查找差不多一样,不累赘)
两种情况
1.左儿子最右边的值<右儿子最左边的值
cntl=(左儿子cntl==左儿子的len)?左儿子的len+右儿子的cntl:左儿子的cntl;
cntr=(右儿子cntl==右儿子的len)?左儿子的cntr+右儿子的len:右儿子的cntr;
cnt=max(左儿子的cntr+右儿子的cntl,左儿子的cnt,右儿子的cnt);
2.左儿子最右边的值>=右儿子最左边的值
cntl=左儿子的cntl;
cntr=右儿子的cntr;
cnt=max(左儿子的cnt,右儿子的cnt);
#include 1|1].fsnm)
{
tree[tn].cntl=
(tree[tn<<1].cntl==tree[tn<<1].len)?(tree[tn<<1].len+tree[tn<<1|1].cntl):tree[tn<<1].cntl;
tree[tn].cntr=
(tree[tn<<1|1].cntr==tree[tn<<1|1].len)?(tree[tn<<1].cntr+tree[tn<<1|1].len):tree[tn<<1|1].cntr;
tree[tn].cnt=max(tree[tn<<1].cnt,tree[tn<<1|1].cnt);
tree[tn].cnt=max(tree[tn].cnt,tree[tn<<1].cntr+tree[tn<<1|1].cntl);
}
else
{
tree[tn].cntl=tree[tn<<1].cntl;
tree[tn].cntr=tree[tn<<1|1].cntr;
tree[tn].cnt=max(tree[tn<<1].cnt,tree[tn<<1|1].cnt);
}
}
void build(int tn,int l,int r)
{
tree[tn].len=r-l+1;
if(l==r) {
scanf("%d",&tree[tn].lsnm);
tree[tn].fsnm=tree[tn].lsnm;
tree[tn].cntl=tree[tn].cntr=tree[tn].cnt=1;
return;
}
int mid=(l+r)>>1;
build(tn<<1,l,mid);
build(tn<<1|1,mid+1,r);
push_up(tn);
}
void update(int tn,int l,int r,int a,int b)
{
if(l==a&&r==a) {
tree[tn].fsnm=tree[tn].lsnm=b;
return;}
int mid=(l+r)>>1;
if(a<=mid) update(tn<<1,l,mid,a,b);
else update(tn<<1|1,mid+1,r,a,b);
push_up(tn);
}
int query(int tn,int l,int r,int yl,int yr)
{
if(yl<=l&&r<=yr) return tree[tn].cnt;
int mid=(l+r)>>1,res;
if(yr<=mid) return query(tn<<1,l,mid,yl,yr);
else if(yl>mid) return query(tn<<1|1,mid+1,r,yl,yr);
else{
res=max(query(tn<<1,l,mid,yl,mid),query(tn<<1|1,mid+1,r,mid+1,yr));
if(tree[tn<<1].lsnm1|1].fsnm)
res=max(res,min(tree[tn<<1].cntr,mid-yl+1)+min(tree[tn<<1|1].cntl,yr-mid));//走右要+1
return res;
}
}
int main(int argc, char const *argv[])
{
int t;
cin>>t;
while(t--)
{
ms(tree);
int n,m;
scanf("%d %d",&n,&m);
build(1,0,n-1);
for(int i=0;ichar ss[3];
int a,b;
scanf("%s %d %d",ss,&a,&b);
if(ss[0]=='U') update(1,0,n-1,a,b);
else printf("%d\n",query(1,0,n-1,a,b) );
}
}
return 0;
}
/*
两个难点: 向上更新和查找
##向上更新
两种情况
1.左儿子最右边的值<右儿子最左边的值
cntl=(左儿子cntl==左儿子的len)?左儿子的len+右儿子的cntl:左儿子的cntl;
cntr=(右儿子cntl==右儿子的len)?左儿子的cntr+右儿子的len:右儿子的cntr;
cnt=max(左儿子的cntr+右儿子的cntl,左儿子的cnt,右儿子的cnt);
2.左儿子最右边的值>=右儿子最左边的值
cntl=左儿子的cntl;
cntr=右儿子的cntr;
cnt=max(左儿子的cnt,右儿子的cnt);
*/ 例题poj3667 HOTEL
这道题真的不错,好好做,比起上一道题多了push_down函数,没错,要用到成端更新。
#include 1].cntr+tree[tn<<1|1].cntl)
{
tree[tn].cnt=tree[tn<<1].cntr+tree[tn<<1|1].cntl;
tree[tn].fs=m-tree[tn<<1].cntr+1;
}
else if(tree[tn].cnt==tree[tn<<1].cntr+tree[tn<<1|1].cntl)
tree[tn].fs=min(tree[tn].fs,m-tree[tn<<1].cntr+1);
}
void build(int tn,int l,int r)
{
tree[tn].len=r-l+1;
if(l==r) {tree[tn].cnt=tree[tn].cntl=tree[tn].cntr=1;
tree[tn].fs=l;
return ;}
int m=(l+r)>>1;
build(tn<<1,l,m);
build(tn<<1|1,m+1,r);
push_up(tn,l,r);
}
void push_down(int tn,int l,int r)
{
int m=(l+r)>>1;
if(tree[tn].lazy){
tree[tn<<1].lazy=tree[tn<<1|1].lazy=tree[tn].lazy;
tree[tn<<1].cntl=tree[tn<<1].cntr=tree[tn<<1].cnt=(tree[tn].lazy==1)?0:tree[tn<<1].len;
tree[tn<<1|1].cntl=tree[tn<<1|1].cntr=tree[tn<<1|1].cnt=(tree[tn].lazy==1)?0:tree[tn<<1|1].len;
tree[tn<<1].fs=(tree[tn].lazy==1)?-1:l;
tree[tn<<1|1].fs=(tree[tn].lazy==1)?-1:(m+1);
tree[tn].lazy=0;
}
}
void add(int tn,int l,int r,int yl,int yr,int flg)
{
if(yl<=l&&r<=yr) {
tree[tn].cnt=tree[tn].cntl=tree[tn].cntr=(flg==1)?0:tree[tn].len;
tree[tn].fs=(flg==1)?-1:l;
tree[tn].lazy=flg;
return ;}
//if(tn==6) printf("%d\n",tree[6].lazy );
push_down(tn,l,r);
//if(tn==6) printf("%d %d %d\n",tree[6].lazy,tree[12].cntl,tree[13].cntl );
int m=(l+r)>>1;
if(yr<=m) add(tn<<1,l,m,yl,yr,flg);
else if(yl>m) add(tn<<1|1,m+1,r,yl,yr,flg);
else{
add(tn<<1,l,m,yl,m,flg);
add(tn<<1|1,m+1,r,m+1,yr,flg);
}
push_up(tn,l,r);
}
int checkin(int tn,int l,int r,int num)
{
if(tree[tn].cnt==num) {
int res=tree[tn].fs;
add(tn,l,r,tree[tn].fs,tree[tn].fs+num-1,1);
return res;}
int m=(l+r)>>1,res;
if(num<=tree[tn<<1].cntl) {res=l;
add(tn,l,r,l,l+num-1,1);}
else if(num<=tree[tn<<1].cnt) res=checkin(tn<<1,l,m,num);
else if(num<=tree[tn<<1].cntr+tree[tn<<1|1].cntl)
{
res= m-tree[tn<<1].cntr+1;
add(tn,l,r,m-tree[tn<<1].cntr+1,m+num-tree[tn<<1].cntr,1);
}
else res= checkin(tn<<1|1,m+1,r,num);
push_up(tn,l,r);
return res;
}
int main(int argc, char const *argv[])
{
int n,m;
cin>>n>>m;
ms(tree);
build(1,1,n);
while(m--)
{
int d;
scanf("%d",&d);
if(d==1){
int a;
scanf("%d",&a);
if(tree[1].cnt"0");
else printf("%d\n",checkin(1,1,n,a) );
}
else {
int a,b;
scanf("%d %d",&a,&b);
add(1,1,n,a,a+b-1,-1);
}
}
return 0;
} 扫描线
扫描线我也是看了两天才会的。
假设向上扫描,每个矩形下边记为1,入边,上边记为-1,出边。
< A1,B1 >首先被扫,更新线段树,接着扫到B2所在的纵轴,是入边,更新线段树并计算这两条扫描线之间的面积,继续扫到A3所在的纵轴,出边,计算这两条扫描线之间的面积,,,,,,
相信不少人看完还是很懵,原理应该能懂吧,我其实也是看代码看懂的。
PS 网上有些代码是错的。
相信有人会不理解这一步。
其实这里线段树每个节点代表的是端点,不是一个线段。
如果代表的是线段,比如父节点1-11,
那左儿子1-6,7-11.这样是对的。
但是当代表的是点时,比如父节点 点1-11
那左儿子1-6,7-11.这样就错了,因为6,7这两个点之间的线段没了!!!
所以只能是1-6,6-11.
build(tn<<1,l,mid);
build(tn<<1|1,mid,r);例题hdu 1542 Atlantis
#include double tx1,ty1,tx2,ty2;
scanf("%lf %lf %lf %lf",&tx1,&ty1,&tx2,&ty2);
line[t].x=tx1,line[t].yy1=ty1,line[t].yy2=ty2;
y[t]=ty1;
line[t++].f=1;
line[t].x=tx2,line[t].yy1=ty1,line[t].yy2=ty2;
y[t]=ty2;
line[t++].f=-1;
}
qsort(line,t,sizeof(struct _Line),cmp);
sort(y,y+t);
build(1,0,t-1);
update(1,&line[0]);
double res=0.0;
for(int i=1;i1].len*(line[i].x-line[i-1].x);
update(1,&line[i]);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",++ti,res );
}
return 0;
} poj1177 picture
这道题需要用到一点技巧,当然x轴扫一边,y轴扫一边也是可以的,就是代码量太大了。
需要标记每个区间左右节点是否会被覆盖。
比如root 1-12
现在近来1-8,那么它会分为
1-6,6-8。此时就会多出一个segnum,所以算1-8会多出1(事实上有可能不止)。但有了标记之后,由于1-6的右节点和6-8的左节点都被覆盖,所以segnum–;
#include int a,b,c,d;
scanf("%d %d %d %d",&a,&b,&c,&d);
line[t].x=a,line[t].yy1=b,line[t].yy2=d;
y[t]=b;line[t++].f=1;
line[t].x=c,line[t].yy1=b,line[t].yy2=d;
y[t]=d;line[t++].f=-1;
}
sort(y,y+t);
int m=unique(y,y+t)-y;
qsort(line,t,sizeof(struct _Line),cmp);
build(1,0,m-1);
update(1,&line[0]);
int ans=mabs(tree[1].len),last=tree[1].len;
for(int i=1;i1].numseg*2*(line[i].x-line[i-1].x);
update(1,&line[i]);
ans+=mabs(tree[1].len-last);
last=tree[1].len;
}
printf("%d\n",ans );
return 0;
} 例题hdu1225覆盖的面积
这道题可以说是altantis的加强版,可以加强对扫描线的理解。
第一个if应该很好理解,
第二个if,tree[tn].more=当前区间整个区间完全覆盖一次(已满足)与两个子区间覆盖一次以上的面积之和。
第三个 if,tree[tn].more便只能等于两个子区间覆盖两次以上的面积和。
void calen(int tn)
{
if(tree[tn].f>1)
{
tree[tn].more=tree[tn].len=tree[tn].rd-tree[tn].ld;
return;
}
if(tree[tn].f>0)
{
tree[tn].len=tree[tn].rd-tree[tn].ld;
if(tree[tn].l+1==tree[tn].r) tree[tn].more=0;
else tree[tn].more=tree[tn<<1].len+tree[tn<<1|1].len;
}
else
if(tree[tn].l+1==tree[tn].r) tree[tn].len=tree[tn].more=0;
else{
tree[tn].len=tree[tn<<1].len+tree[tn<<1|1].len;
tree[tn].more=tree[tn<<1].more+tree[tn<<1|1].more;
}
}#include double a,b,c,d;
scanf("%lf %lf %lf %lf",&a,&b,&c,&d);
line[t].x=a,line[t].yy1=b,line[t].yy2=d;
line[t].f=1;
y[t++]=b;
line[t].x=c,line[t].yy1=b,line[t].yy2=d;
line[t].f=-1;
y[t++]=d;
}
qsort(line,t,sizeof(struct _Line),cmp);
sort(y,y+t);
int nt=unique(y,y+t)-y;
build(1,0,nt-1);
update(1,&line[0]);
double res=0.0;
for(int i=1;i1].more*(line[i].x-line[i-1].x);
update(1,&line[i]);
}
printf("%.2f\n",res );
}
return 0;
} hdu5091Beam Cannon
组队赛遇到这道题完全没想到用扫描线,还以为是计算几何的题,太弱了。
题意:给n个点,和长w宽h的矩形,问矩形最多能包含多少个点。
思路:对于每一个点(x,y),转化为(x,y)–(x,y+h)线段,入边,标记为1。
并且再加(x+w,y)–(x+w,y+h)线段,出边,标记为-1。
排序后x轴从左往右扫,然后维护区间内点最大的覆盖次数。
(有点难想到,我太弱了)
这道题和前面的题不一样,
之前的题
看这里,
build(tn<<1,l,mid);
build(tn<<1|1,mid,r);而这道题
build(tn<<1,l,md);
build(tn<<1|1,md+1,r);为什么?
之前tree存的是节点,维护的是区间的长度
而这道题tree存的是节点,维护的是区间中的点最大覆盖次数。
#include int x0,y0;
scanf("%d %d",&x0,&y0);
node[i].x=x0;
node[i].y1=y0;
node[i].y2=y0+h;
node[i].flg=1;
y[i+1]=y0;
node[n+i].x=x0+w;
node[n+i].y1=y0;
node[n+i].y2=y0+h;
node[n+i].flg=-1;
y[n+i+1]=y0+h;
}
qsort(node,2*n,sizeof(struct _Node),cmp);
sort(y+1,y+2*n+1);
int nnn=unique(y+1,y+2*n+1)-y-1;
build(1,1,nnn);
int ans=0;
for(int i=0;i<2*n;i++)
{
update(1,1,nnn,node[i].y1, node[i].y2,node[i].flg);
ans=max(ans,tree[1].ma_x);
}
printf("%d\n",ans );
}
return 0;
} 当初我也以为这样就以为理解扫描线了,其实不然。
(欢迎指出错误)
一道题:
大意:给出一个多边形,他的每一条边要么平行y轴要么平行x轴,点的顺序按边依次给出,最后一个点与第一个点是最后一条边。
例如: 0.0,0.0
1.0,0.0
1.0,1.0
0.0,1.0
就是一个正方形左下顶点0.0,0.0;右上顶点1.0,1.0;
求这个多边形的面积。
数据范围: 点的个数<=30000,x,y<=1e8.(x,y为浮点数)
如果直接用扫描线做会发现线段树基本不更新,23333.(当然你得先搞定那些边是入边,那些边是出边)
为什么呢?就是那个calen函数的原因,它只能对矩形这种出边和入边在扫描线上是一样的。
如果是x -3 y1 3 y2 13 (入边)1
扫到这条线后线段树的root长度更新为13-3=10
x -2 y1 3 y2 5(出边)-1
扫到这条线后线段树的root长度本来应更新为10-(5-3)=8.
但是事实上仍等于10.
那么扫描线就废了吗?不是还成段更新吗?
对,鄙人的想法就是用成段更新来做。
以下是鄙人的代码
#include else line[t].yy1=d,line[t].yy2=b;
line[t++].f=1;
y[yt++]=b;
y[yt++]=d;
for(int i=2;i2)
{
int x0,y0,xx0,yy0;
scanf("%d %d %d %d",&x0,&y0,&xx0,&yy0);
line[t].x=x0;
if(y0else line[t].yy1=yy0,line[t].yy2=y0;
line[t++].f=(mf*(yy0-y0))>0?1:-1;
y[yt++]=y0;
y[yt++]=yy0;
}
}
else {
int e,f;
scanf("%d %d",&e,&f);
mf=f-d;
line[t].x=e;
if(delse line[t].yy1=f,line[t].yy2=d;
line[t++].f=1;
y[yt++]=d;
y[yt++]=f;
for(int i=3;i1;i+=2)
{
int x0,y0,xx0,yy0;
scanf("%d %d %d %d",&x0,&y0,&xx0,&yy0);
line[t].x=x0;
if(y0else line[t].yy1=yy0,line[t].yy2=y0;
line[t++].f=(mf*(yy0-y0))>0?1:-1;
y[yt++]=y0;
y[yt++]=yy0;
}
scanf("%d %d",&e,&f);
line[t].x=e;
if(belse line[t].yy1=f,line[t].yy2=b;
line[t++].f=(mf*(b-f))>0?1:-1;
y[yt++]=f;
y[yt++]=b;
}
qsort(line,t,sizeof(struct _Line),cmp);
if(line[0].f==-1) {
for(int i=0;iint nt=unique(y,y+yt)-y;
build(1,0,nt-1);
update(1,&line[0]);
int ans=0;
for(int i=1;i1].len*(line[i].x-line[i-1].x);
update(1,&line[i]);
}
printf("%d\n",ans);
}
return 0;
}
/*
1//测试样例个数
10//点的数量
0 0
4 0
4 1
3 1
3 3
2 3
2 2
1 2
1 3
0 3
1
10
0 0
0 3
1 3
1 2
2 2
2 3
3 3
3 1
4 1
4 0
1
4
0 0
0 1
2 1
2 0
1
4
0 0
2 0
2 1
0 1
1
4
10 10
10 20
20 20
20 10
1
6
0 0
0 2
2 2
2 1
3 1
3 0
1
6
0 0
0 1
3 1
3 2
4 2
4 0
1
8
0 0
2 0
2 2
0 2
0 3
-1 3
-1 -1
0 -1
*/