qcwlmqy

ACM数论基础详细整理

目录

质数

质数的判定

试除法

MillerRobbin(米勒罗宾素数测试)

素数筛法

埃氏筛

线性筛

区间筛

Prime Distance

HDU6069 Counting Divisors（区间分解质因数）

阶乘分解

ural1055 Combinations

约数

算术基本定理的扩展

数值分块

BZOJ1257 余数之和

BZOJ2956 模积和

最大公约数

欧几里得算法

区间GCD

HDU 5726 GCD

HDU 5869 Different GCD Subarray Query

欧拉函数

POJ2478 Farey Sequence

POJ3090 Visible Lattice Points

POJ2480 Longge's problem

BZOJ 4804 欧拉心算心酸

HDU5780 gcd

HDU4676 Sum Of Gcd

同余

同余类

剩余系

POJ2773 Happy 2006

欧拉定理

欧拉定理推论

UVA106992 Huge Mods

HDU2837 Calculation

裴蜀定理

扩展欧几里得算法

POJ2115 Looooops

POJ1061 青蛙的约会

同余不等式

POJ3530 A Modular Arithmetic Challenge

线性同余方程组

中国剩余定理

非互质线性同余方程组

POJ2891 Strange Way to Express Integers

GCD Table

高次同余方程

BSGS算法

bzoj2242 [SDOI2011]计算器

原根与指标

例题代码

Prime Distance 代码

Counting Divisors代码

Combinations代码

余数之和代码

模积和代码

斐波那契公约数代码

GCD代码

Different GCD Subarray Query代码

Farey Sequence代码

Visible Lattice Points代码

Longge's problem代码

欧拉心算代码

gcd代码

Sum Of Gcd代码

Happy 2006代码

Huge Mods代码

Calculation代码

Looooops代码

青蛙的约会代码

A Modular Arithmetic Challenge代码

Strange Way to Express Integers代码

GCD Table代码

[SDOI2011]计算器代码

质数

质数的判定

试除法

若一个正整数 N 为合数，则一定存在一个能整除 N 的数字 $2 \leqslant T\leq \sqrt{N}$

MillerRobbin(米勒罗宾素数测试)

大于2的素数n，存在，d为奇数

以下任一条件成立，n为素数,a为任意整数

$a^d\equiv 1\mod n$

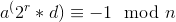
$a^(2^r*d)\equiv-1\mod n$ $0\leq r\leq s-1$

typedef long long LL;
bool check(LL a, LL n) {
	LL m = n - 1, x, y;
	int i, j = 0;
	while (~m & 1)m >>= 1, j++;
	x = quickpow(a, m, n);		//快速幂
	for (i = 1; i <= j; x = y, i++) {
		y = quickpow(x, 2, n);
		if (y == 1 && x != 1 && x != n - 1)
			return true;
	}
	return y != 1;
}
bool miller_rabin(int times, int n) {
	LL a;
	if (n == 1)return false;
	if (n == 2) return true;
	if (~n & 1)return false;
	while (times--)
		if (check(rand() % (n - 1) + 1, n))
			return false;
	return true;
}

素数筛法

埃氏筛

任意x的倍数都不是素数

线性筛

埃式筛法对同一个合数多次标记导致耗时非线性，比如

线性筛法通过唯一标记合数的方式来优化埃氏筛

for (int i = 2; i <= N; i++) {
	if (!vis[i])prime[cnt++] = i;
	for (int j = 0; j < cnt&&prime[j] * i <= N; j++) {
		vis[prime[j] * i] = true;
		if (i%prime[j] == 0)
			break;
	}
}

区间筛

一个合数 n 一定包含一个不超过 $\sqrt{n}$ 的质因数

用筛法求出 $\sqrt{Max}$ 以内的质数

用这些质数去标记 [L,R] 中的合数，未被标记的就是质数

const int maxm = 1000000;
bool v[maxm];
void interval_sieve(int l, int r) {
    memset(v,0,sizeof(v));
	if (l == 1)v[0] = true;
	for (int i = 0; i < cnt; i++) {
		for (int j = (l - 1) / prime[i] + 1; j <= r / prime[i]; j++) {
			if (j > 1) v[prime[i] * j - l] = true;
		}
	}
}

Prime Distance

给定整数L，R，求区间相邻两个质数的差最大是多少？

板子题

HDU6069 Counting Divisors（区间分解质因数）

求 $\sum_{i=1}{d(i^k)}\mod998244353$

积性函数

因子数

则

本题要用到区间筛法对L-R分解质因数

阶乘分解

阶乘 N！中包含质因子 x 的个数为 $\frac{N}{x}+\frac{N}{x^2}+\cdots+\frac{N}{x^n}$

ural1055 Combinations

求 Cm n (1 ≤n,m≤ 5∗105) 的不同质因子个数

$C\binom{n}{m}=\frac{n!}{(n-m)!*m!}$

分别求分子质因子个数和分母质因子个数，若分子个数比分母多则有效

约数

算术基本定理的扩展

约数个数

约数之和 $=(1+p_{1}+p_{1}^2+\cdots+p_{1}^c_{1})+(1+p_{2}+p_{2}^2+\cdots+p_{2}^c_{2})+\cdots+(1+p_{n}+p_{n}^2+\cdots+p_{n}^c_{n})$

数值分块

BZOJ1257 余数之和

给定正整数n，k，计算

$k \mod 1 + k \mod 2 + k \mod 3 + --- + k \mod n$

$k \mod i = k - k / i * i$

当 $i<\sqrt(k)$ 时，最多只有 $\sqrt{k}$ 个取值

当 $i>\sqrt{k}$ 时，最多只有 $\sqrt{k}$ 个取值

综上最多只有 $2\sqrt{k}$ 个取值，且数值单调递减，可以数值分块

BZOJ2956 模积和

求 $\sum_{i=1}^{n}\sum_{j=1}^{m}((n \mod i)*(m \mod j)) (i \neq j)$

$=\sum_{i=1}^{n} (n\mod i)*\sum_{j=1}^{m}(m \mod i)-\sum_{i=1}^{min(n,m)}(n \mod i)*(m \mod i)$

第一项与第二项与上题同

$=\sum_{i=1}^{min(n,m)}(n-n/i*i)*(m-m/i*i)$

$=\sum_{i=1}^{min(n,m)}(n*m-m*n/i*i-n*m/i*i+n/i*i*m/i*i)$

最大公约数

$\gcd (Fib(n),Fib(m))=\gcd(Fib(n-m),Fib(m))$

$\gcd(m^a,n^a)=\gcd(m,n)^a$

$gcd(a^m-b^m,a^n-b^n)=a^{gcd(m,n)}-b^{gcd(m,n)}$ （a,b互质）

欧几里得算法

$gcd(a.b)=gcd(b,a\mod b)$

设 a = q∗b+r，其中 r = a mod b

对于 a，b 的任意公约数 d，d|a，d|q*b

则 d|(a-q*b)，即 d|r

int gcd(int a,int b){
    return b? gcd(b,a%b):a;}
}

区间GCD

当固定区间的右端点，区间左端点越小，区间的GCD就越小，区间GCD的变化次数至多等于右端点的质因子数

a1=1, a2=2, a3=4, a4=6

从小到大枚举右端点，计算左端点的分界线,表示对于右端点,左端点属于时区间gcd都是相同的

$l[4]=4:gcd(j,4)=4(4\leq j\leq 4)$

$l[3]=2:gcd(j,4)=2(2\leq j\leq 3 )$

$l[1]=1:gcd(j,4)=1(1\leq j\leq 1 )$

在枚举的过程中，可以利用右端点在时数组的计算结果，因为区间内多一个数字时，区间GCD的段数单调不增，可以通过右端点在时候的分段合并得到

a5=9

复杂度

//a[i]为数组
//l[j]表示l[j]-j的区间gcd相同
//v[j]表示l[j]-j的区间gcd的值
for (int i = 1; i <= n; i++) {
	for (v[i] = a[i], j = l[i] = i; j; j = l[j] - 1) {    //通过l[j]移动
		v[j] = gcd(v[j], a[i]);
		while (l[j] > 1 && gcd(a[i], v[j] - 1) == gcd(a[i], v[j]))    //若两个区间gcd相同则合并
			l[j] = l[l[j] - 1];
	}
}

HDU 5726 GCD

给出数组a，询问L，R的区间gcd的值和与L，R区间gcd相同的组数

枚举i的右端点，将所有的l[j]和v[j]分别存储（本题相同值的组数要开longlong！！！）

HDU 5869 Different GCD Subarray Query

求L-R区间内区间gcd的值的数量

转化为求区间内颜色数量的问题，可以用离线树状数组或者主席树做，不会的可以看道例题学习下，洛谷 HH的项链

那么这题需要考虑的是怎么把区间的颜色转化到点上？

我们通过区间gcd可以知道L【j】- j的颜色，即只要包含右边界，就可以取到x

所以增加一个区间，相当于j点增加一种颜色

欧拉函数

欧拉函数 ϕ(N)：1 到 N 中与 N 互质的数字个数

$\Theta (N)=N*\frac{p_{1}}{p_{1}-1}*\frac{p_{2}}{p_{2}-1}*\cdots*\frac{p_{n}}{p_{n}-1}$

$gcd(n,m)=1->\Theta (n*m)=\Theta(n)*\Theta(m)$

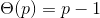
对于质数p， $\Theta (p)=p-1$

若a为质数, $\Theta(b*a)=\Theta(b)*a(b\mod a==0)$

//什么意思我也不懂 qwq

大概意思应该是n的所有因数的欧拉函数和为n

分解质因数求欧拉函数

int phi(int n){
	int ans=n;
	for(int i=2;i*i<=n;i++){
		if(n%i==0){
			ans=ans/i*(i-1);
			while(n%i==0) n/=i;
		}
	}
	if(n>1) ans=ans/n*(n-1);
	return ans;
}

线性筛求质因数

/*
特性 :
1.若a为质数,phi[a]=a-1;
2.若a为质数,b mod a=0,phi[a*b]=phi[b]*a
3.若a,b互质,phi[a*b]=phi[a]*phi[b](当a为质数时,if b mod a!=0 ,phi[a*b]=phi[a]*phi[b])
*/
bool vis[maxn+5];
int prime[maxn+5],cnt;
int phi[maxn+5];
void Phi() {
	phi[1]=1;
	vis[1]=true;
	for(int i=2; i<=maxn; i++) {
		if(!vis[i]) prime[cnt++]=i,phi[i]=i-1;
		for(int j=0; j

 
  POJ2478 Farey Sequence 
  求n以内的互质数对 
  欧拉函数求和，板子题 
    
  POJ3090 Visible Lattice Points 
  二维坐标站在（0，0）点上，能看到第一象限哪些点 
  看到的点的x,y都是互质的，考虑x,y轴和对角线 
    
  POJ2480 Longge's problem 
  求 
  枚举GCD 
  统计的个数，发现其个数为 
  因为x为N的因数，gcd（i，N）=x，i应与互质 
   
  欧拉函数是非完全积性函数，积性函数的约数和也是积性函数 
   
   
  若a为质数,b mod a=0,phi[a*b]=phi[b]*a 
   
   
  BZOJ 4804 欧拉心算   心酸 
  求 
  统计的个数，为 
  即若gcd(i,j)==x,则与互质 
  与上文中的Visible Lattice Points很像，即为二维坐标上互质的点， 
  综上，结论为,在来一波等值分块就能过了 
    
  HDU5780 gcd 
  求 
  先套一波上面的公式 
  同上题，取 
  并等值分块 
    
  HDU4676 Sum Of Gcd 
  求L和R， 
  一道RMQ问题，明显树状数组和线段树什么的无法维护，但可以用莫队做 
  那么我们只需要考虑莫队的转移就好 
  若d1----dn为n的所有因数， 
  设d1----dn为gcd(a[i],a[j]）的因数， 
  比如2，4，有cnt[1]=2,cnt[2]=2,cnt[4]=1,因为约数1，2出现两次，1、2为公约数，phi[1]+phi[2]=2=gcd(2,4) 
  若已知cnt[d]=x,x中任选2个，可以成为gcd（a[i],a[j]）的公约数 
  所以我们统计约数个数就能计算出a[j]与a[1]----a[j-1]的gcd之和 
    
  同余 
   
   若,则称a,b模m同余  
   
    
  同余类 
   
   将相同的数归入一个集合，称为同余类 
   
    
  剩余系 
   
   m 的 m 个同余类称为完全剩余系 
   所有与 m 互质的同余类称为简化剩余系 
   简化剩余系乘法封闭，若 a，b 分别和 m 互质，则 a*b 也 和 m 互质 
   
  POJ2773 Happy 2006 
  求与n互质的第k小的数字  
   
  同理， 
  如题，若 
  以n为周期，求余，暴力第k小 
  欧拉定理 
   
   若正整数 a,n 互质，有  
   
    
  欧拉定理推论 
   
   若正整数a,p互质，则对于正整数b

 当正整数 a,p 不一定互质时
 
   
    
  UVA106992 Huge Mods 
  求 
  欧拉降幂板子题 
    
    
  HDU2837 Calculation 
   
  同上题 
    
  裴蜀定理 
   
   对于任意正整数a,b，存在一对整数x,y满足 
   
    
  扩展欧几里得算法 
   
   证明裴蜀定理的过程求出了 x 和 y，这个计算方法称为扩展欧几里得算法 
   代码求出了 gcd(a,b)，并得到了 ax+by=gcd(a,b) 的一组特 解，x 和 y 需要以引用方式传入 
   
  //ax1+ by1= gcd(a,b);
//bx2 + (a mod b)y2 = gcd(b, a mod b);
//ax1 + by1 = bx2 + (a - [a / b] * b)y2 = ay2 + bx2 - [a / b] * by2;
//x1 = y2; y1 = x2 - [a / b] * y2;
LL gcd(LL a, LL b, LL &x, LL & y)
{
	if (b == 0) {
		x = 1, y = 0;
		return a;
	}
	int q = gcd(b, a%b, y, x);
	y -= a / b * x;
	return q;
} 
  POJ2115 Looooops 
  求以下程序段的循环次数，其中变量为 k 位无符号整数  
  for (variable = A; variable != B; variable += C) 
   
   
   
  特解： 
  要 
  最小解：注意负数 
    
  POJ1061 青蛙的约会 
  简直和上一题一模一样 
    
  同余不等式 
  POJ3530 A Modular Arithmetic Challenge 
  求x使得 
   
   
   
  y越小-->x越小 
  两边求余 
    
  线性同余方程组 
  中国剩余定理 
   
   两两互质，, 
   是线性同余方程的一个解 
   对于任意n个整数,方程组 
        
        
        
        
    
   
  for (int i = 1; i <= n; i++) {
		M[i] = M / m[i];
		d = gcd(m[i], M[i], x, y);
		ans += y * m[i] * M[i];
	} 
    
  非互质线性同余方程组 
   
   以1、2两式为例 
    
     
     
    
   两边求余 
   ，扩展欧几里得求解 
   将带会  式 
   且满足1，2两式 
    
   
  LL CRT() {
	LL m1, m2, a1, a2, x, y, c;
	m1 = m[1]; a1 = a[1];
	bool flag = true;
	for (int i = 2; i <= k; i++) {
		m2 = m[i]; a2 = a[i];
		c = exgcd(m1, m2, x, y);
		if ((a2 - a1) % c)
			flag = false;
		x = (a2 - a1) / c * x;
		y = m2 / c;
		x = (x % y + y) % y;
		a1 = x * m1 + a1;
		m1 = (m1 * m2) / c;
	}
	c = exgcd(1, m1, x, y);
	if (a1 % c) flag = false;
	if (!flag)
		return -1;
	x = a1 / c * x;
	y = m1 / c;
	x = (x % y + y) % y;
	return x;
} 
    
  POJ2891 Strange Way to Express Integers 
  板子题 
    
  GCD Table 
  题解链接 
    
  高次同余方程 
   
   给定整数,求一个非负整数x，使得 
   
    
  BSGS算法 
   
   设,其中是步长，这里取, 
   方程变为 
   即 
   将存入哈希表，枚举i,计算是否存在于哈希表中，即可更新答案 
   此处链接一位大神的博客 
   
  int bsgs(int a, int b, int p) {
	map H;
	H.clear();
	b %= p;
	int t = (int)sqrt(p) + 1;
	for (int i = 0; i < t; i++) {
		int val = (LL)b * quickpow(a, i, p) % p;
		H[val] = i;
	}
	a = quickpow(a, t, p);
	if (!a) return b ? -1 : 1;
	for (int i = 0; i <= t; i++) {
		int val = quickpow(a, i, p);
		int j = H.find(val) == H.end() ? -1 : H[val];
		if (j >= 0 && i * t >= j) return i * t - j;
	}
	return -1;
} 
  bzoj2242  [SDOI2011]计算器 
  板子题 
    
  原根与指标 
  知识点链接 
    
  例题代码 
  Prime Distance 代码 
  #include 
#include 
#include 
#include 
using namespace std;
const unsigned int max = 1 << 31;
const unsigned int maxn = 50000;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
bool vis[maxn + 5];
unsigned int prime[maxn + 5], cnt = 0;
void Init() {        //预处理<=R的素数
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = true;
			if (i % prime[j] == 0)break;
		}
	}
}
const unsigned int maxm = 1000000;
bool v[maxm + 10];
void interval_sieve(unsigned int l, unsigned int r) {    //区间筛
	unsigned int limit = sqrt(r * 1.0) + 1;
	if (l == 1)v[0] = true;
	for (int i = 0; i < cnt; i++) {
		if (prime[i] > limit) break;
		for (int j = (l - 1) / prime[i] + 1; j <= r / prime[i]; j++) {
			if (j > 1) v[prime[i] * j - l] = true;
		}
	}
}
int main() {
	Init();
	unsigned int l, r;
	while (cin >> l >> r) {
		interval_sieve(l, r);
		unsigned int p = 0, a = 0, b = 0, c = 0, d = 0, min = r - l + 1, max = 0;
		while (v[p])p++;
		bool flag = false;
		for (unsigned int i = p + 1; i <= r - l; i++) {
			if (!v[i]) {
				flag = true;
				if (i - p < min)
					a = p, b = i, min = i - p;
				if (i - p > max)
					c = p, d = i, max = i - p;
				p = i;
			}
		}
		if (!flag)printf("There are no adjacent primes.\n");
		else printf("%d,%d are closest, %d,%d are most distant.\n", a + l, b + l, c + l, d + l);
		fill(v, v + r - l + 10, 0);
	}
} 
  Counting Divisors代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
inline void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
const LL mod = 998244353;
const int maxn = 1000010;
bool vis[maxn + 5];
int prime[maxn + 5], cnt = 0;
void Prime() {
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i])prime[cnt++] = i;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = true;
			if (prime[j] % i == 0)break;
		}
	}
}
LL k, num[maxn], d[maxn];
void slove(LL l, LL r) {
	LL limit, g;
	limit = sqrt(r * 1.0) + 1;
	for (int i = 0; i < cnt; i++) {
		if (prime[i] > limit)break;
		LL s = (l + prime[i] - 1) / prime[i] * prime[i];
		for (LL j = s; j <= r; j += prime[i]) {    //用类似筛法的方法压缩时间
			if (num[j - l] % prime[i] == 0) {
				g = 0;
				while (num[j - l] % prime[i] == 0) {
					num[j - l] /= prime[i];
					g++;
				}
				d[j - l] = d[j - l] * (k * g + 1) % mod;
			}
		}
	}
}
int main() {
	io(); Prime();
	int t;cin >> t;
	while (t--){
		LL l, r;
		cin >> l >> r >> k;
		for (int i = 0; i <= r - l; i++)
			num[i] = i + l, d[i] = 1;
		slove(l, r);
		LL ans = 0;
		for (int i = 0; i <= r - l; i++) {
			if (num[i] > 1) {
				d[i] = d[i] * (k + 1) % mod;
			}
			ans += d[i]; ans %= mod;
		}
		cout << ans << '\n';
	}
} 
    
  Combinations代码 
  #include 
#include 
using namespace std;
const int maxn = 50005;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
void Prime() {
	prime[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i])prime[cnt++] = i;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = true;
			if (prime[j] % i == 0)break;
		}
	}
}
int GetNum(int N, int x) {
	int res = 0, m = x;
	while (N >= m) {
		res += N / m;
		m *= x;
	}
	return res;
}
int main() {
	io(); Prime();
	int n, m;
	while (cin >> n >> m) {
		int k = n - m, ans = 0, limit = n;
		for (int i = 0; i < cnt; i++) {
			if (prime[i] > limit)break;
			if (GetNum(n, prime[i]) - GetNum(k, prime[i]) - GetNum(m, prime[i]) > 0)
				ans++;
		}
		printf("%d\n", ans);
	}
} 
  余数之和代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
}
// k mod i= k - k / i * i
int main() {
	io();
	LL ans, n, k, r;
	cin >> n >> k;
	ans = n * k;
	n = min(n, k);
	for (LL l = 1; l <= n; l = r + 1) {
		LL u = k / l;
		r = min(k / u, n);
		ans -= (l + r) * (r - l + 1) / 2 * u;
	}
	cout << ans << '\n';
} 
  模积和代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
}
LL mod = 19940417;
LL inv[8];    //求逆元
void init() {
	inv[1] = 1;
	for (LL i = 2; i <= 6; i++) {
		inv[i] = (mod - mod / i) * (LL)1 * inv[mod % i] % mod;
	}
}
// k mod i= k - k / i * i
LL GetNum(LL n) {        //区间分块
	LL ans = n * n % mod, r;
	for (LL l = 1; l <= n; l = r + 1) {
		LL u = n / l;
		r = min(n / u, n);
		ans = ans - (l + r) * (r - l + 1)/2 % mod * u % mod;
	}
	return ans % mod;
}
//sum(i,min(n,m))=(n*m-m*n/i*i-n*m/i*i+n/i*i*m/i*i)
int main() {
	io(); init();
	LL n, m, res;
	cin >> n >> m;
	res = GetNum(n) * GetNum(m) % mod;
	if (n > m)swap(n, m); 
	LL cnt = n * m % mod * n % mod;
	for (LL l = 1, r; l <= n; l = r + 1) {
		r = min(n / (n / l), m / (m / l));     //选择较小的块移动
		cnt += (n / l) * (m / l) % mod * ((r * (r + 1) % mod * (2 * r + 1) % mod * inv[6] % mod) - ((l - 1) * l % mod * (2 * l - 1) % mod * inv[6] % mod) + mod) % mod;
		cnt -= m / l * n % mod * ((l + r) * (r - l + 1)/2 % mod); if (cnt < 0)cnt += mod;
		cnt -= n / l * m % mod * ((l + r) * (r - l + 1)/2 % mod); if (cnt < 0)cnt += mod;
	}
	res -= cnt; res %= mod; if (res < 0)res+=mod;
	cout << res << '\n';
} 
  斐波那契公约数代码 
  #include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long int LL;
const LL mod = 1e8;
LL res[3][3] = { 0,0,0,0,1,1 }, r[3][3] = { 0,0,0,0,0,1,0,1,1 }, t[3][3];
LL gcd(LL a, LL b)
{
	LL c;
	while (c = a % b)
	{
		a = b;
		b = c;
	}
	return b;
}
void mul(LL res[3][3], LL m[3][3], LL h)
{
	for (int i = 1; i <= h; i++)
		for (int j = 1; j <= 2; j++)
			t[i][j] = (res[i][1] * m[1][j] % mod + res[i][2] * m[2][j] % mod) % mod;
	for (int i = 1; i <= h; i++)
		for (int j = 1; j <= 2; j++)
			res[i][j] = t[i][j];
}
void quickmul(LL p)
{
	while (p)
	{
		if (p & 1)
			mul(res, r, 1);
		mul(r, r, 2);
		p >>= 1;
	}
}
int main()
{
	LL n, m;
	scanf("%lld%lld", &n, &m);
	LL cnt = gcd(n, m);
	if (cnt == 1 || cnt == 2)
		printf("1\n");
	else
	{
		quickmul(gcd(n, m) - 2);
		printf("%lld\n", res[1][2]);
	}
} 
  GCD代码  
  #include 
#include 
#include 
#include 
#include 
using namespace std;
typedef pair pii;
typedef long long LL;
const int maxn = 100005;
map Map;
vector E[maxn];
int gcd(int a, int b) {
	int c;
	while (c=a%b){
		a = b;
		b = c;
	}
	return b;
}
int a[maxn], l[maxn], v[maxn];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int t, g = 0, n, q; cin >> t;
	while (t--){
		cout << "Case #" << ++g << ":\n";
		cin >> n;
		for (int i = 1; i <= n; i++)cin >> a[i];
		int j;
		for (int i = 1; i <= n; i++) {
			for (v[i] = a[i], j = l[i] = i; j; j = l[j] - 1) {
				v[j] = gcd(v[j], a[i]);
				while (l[j] > 1 && gcd(a[i], v[l[j] - 1]) == gcd(a[i], v[j]))
					l[j] = l[l[j] - 1];
				E[i].push_back(pii(l[j], v[j]));
				Map[v[j]] += LL(j - l[j] + 1);
			}
		}
		cin >> q;
		int L, R;
		for (int i = 1; i <= q; i++) {
			cin >> L >> R;
			//cout << r << '\n';
			for (int j = 0; j < E[R].size(); j++) {
				if (L >= E[R][j].first) {
					cout << E[R][j].second << ' ' << Map[E[R][j].second] << '\n';
					break;
				}
			}
		}
		for (int i = 0; i <= n; i++) {
			E[i].clear(); 
			l[i] = v[i] = 0; 
		}
		Map.clear();
	}
} 
  Different GCD Subarray Query代码 
  #include 
#include 
#include 
#include 
using namespace std;
const int maxn=100005;
int gcd(int a,int b) {
	return b==0?a:gcd(b,a%b);
}
int n,q;
int tree[maxn];
inline int lowbit(int x) {
	return x & -x;
}
void update(int x, int value) {
	while (x <= n) {
		tree[x] += value;
		x += lowbit(x);
	}
}
int query(int x) {
	int ans = 0;
	while (x) {
		ans += tree[x];
		x -= lowbit(x);
	}
	return ans;
}
int a[maxn],l[maxn],v[maxn];
map Map;
void modify(int i) {
	int j;
	for (v[i] = a[i], j = l[i] = i; j; j = l[j] - 1) {
		v[j] = gcd(v[j], a[i]);
		while (l[j] > 1 && gcd(a[i], v[l[j] - 1]) == gcd(a[i], v[j]))
			l[j] = l[l[j] - 1];
		int p=Map[v[j]];
		if(p==0) {
			update(j,1);
		} else if(p!=j) {
			update(p,-1);
			update(j,1);
		}
		Map[v[j]]=j;
	}
}
struct node {
	int left;
	int right;
	int ops;
	friend bool operator <(node &a,node &b) {
		return a.right>n>>q) {
		for(int i=1; i<=n; i++)cin>>a[i];
		for(int i=1; i<=q; i++) {
			cin>>line[i].left>>line[i].right;
			line[i].ops=i;
		}
		sort(line+1,line+1+q);
		int next=1;
		for(int i=1; i<=q; i++) {
			while(next<=line[i].right) {
				modify(next);
				next++;
			}
			res[line[i].ops]=query(line[i].right)-query(line[i].left-1);
		}
		for(int i=1; i<=q; i++)
			cout<
 
  Farey Sequence代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 1000005;
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
int phi[maxn + 5];
void Phi() {
	phi[1] = 1;
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}
LL sum[maxn+5];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	Phi(); phi[1] = 0;
	for (int i = 1; i <= maxn; i++)
		sum[i] = sum[i - 1] + phi[i];
	int n;
	while (cin>>n&&n)
		cout << sum[n] << '\n';
} 
  Visible Lattice Points代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 1005;
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
int phi[maxn + 5];
void Phi() {
	phi[1] = 1;
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}
int sum[maxn + 5];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	Phi(); phi[1] = 0;
	for (int i = 1; i <= maxn; i++)
		sum[i] = sum[i - 1] + phi[i];
	int n, x, g = 0; cin >> n;
	while (n--) {
		cin >> x;
		cout << ++g << ' ' << x << ' ' << 2 * sum[x] + 3<
 
  Longge's problem代码 
  //推导见数论博客
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 47000;
bool vis[maxn + 5];
int prime[maxn + 5], cnt = 0;
void Prime() {
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i;
		for (int j = 0; j < cnt && i * prime[j] <= maxn; j++) {
			vis[prime[j] * i] = true;
			if (i % prime[j] == 0)break;
		}
	}
}
void slove(int n) {
	int limit = sqrt(n * 1.0) + 1;
	LL ans = 1;
	int m, g;
	for (int i = 0; i < cnt; i++) {
		if (prime[i] > limit) break;
		if (n % prime[i] == 0) {
			m = n; g = 0;
			while (n % prime[i] == 0) {
				n /= prime[i];
				g++;
			}
			ans = ans * (LL(m) / n / prime[i] * g * (prime[i] - 1) + m / n);
		}
	}
	if (n > 1) ans = ans * (LL(2) * n - 1);
	cout << ans << '\n';
}
int main() {
	Prime();
	int n;
	while (cin >> n)
		slove(n);
} 
  欧拉心算  代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 10000005;
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
int phi[maxn + 5];
LL sum[maxn + 5];
void Phi() {
	phi[1] = 1;
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
	for (int i = 1; i <= maxn; i++)
		sum[i] = sum[i - 1] + phi[i];
}
//Sum(phi[x])*2*Sum(phi[n/x])-1)
void slove(int n) {
	LL ans = 0;
	for (int l = 1, r; l <= n; l = r + 1) {
		int u = n / l;
		r = n / u;
		ans += (sum[r] - sum[l - 1]) * (sum[u] * 2 - 1);
	}
	cout << ans << '\n';
}
int main() {
	Phi(); 
	int t, n;
	cin >> t;
	while (t--){
		cin >> n;
		slove(n);
	}
} 
  gcd代码 
  #include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 1000005;
const LL mod = 1e9 + 7;
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
int phi[maxn + 5];
LL sum[maxn + 5];
void Phi() {
	phi[1] = 1;
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
	for (int i = 1; i <= maxn; i++) {
		sum[i] = sum[i - 1] + phi[i];
		sum[i] %= mod;
	}
}
LL quickpow(LL x,LL k) {
	LL res = 1, m = x;
	while(k){
		if (k & 1) res *= m, res %= mod;
		m *= m; m %= mod;
		k >>= 1;
	}
	return res;
}
LL GetSum(LL x, LL l, LL r) {
	LL inv = quickpow(x - 1, mod - 2);
	LL ans = quickpow(x, l) * ((quickpow(x, r - l + 1) - 1 + mod) % mod) % mod * inv % mod;
	ans = ans - (r - l + 1) + mod; ans %= mod;
	return ans;
}
//Sum(x^k-1)*2*Sum(phi[n/x])-1)
void slove(LL x, LL n) {
	LL ans = 0;
	for (LL l = 1, r; l <= n; l = r + 1) {
		LL u = n / l;
		r = n / u;
		ans += GetSum(x, l, r) * ((sum[u] * 2 - 1) % mod) % mod;
		ans %= mod;
	}
	cout << ans << '\n';
}
int main() {
	Phi();
	int t, n, x;
	cin >> t;
	while (t--) {
		cin >> x >> n;
		if (x == 1) {
			cout << "0\n";
			continue;
		}
		slove(x, n);
	}
} 
  Sum Of Gcd代码 
  #include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
const int maxn = 20005;
int E[maxn + 5][233];
void Init() {
	int cnt;
	for (int i = 1; i < maxn; i++) {
		cnt = 0;
		for (int j = 1; j * j <= i; j++) {
			if (i % j == 0) {
				E[i][++cnt] = j;
				if (j * j != i)
					E[i][++cnt] = i / j;
			}
		}
		E[i][0] = cnt;
	}
}
bool vis[maxn + 5];
int prime[maxn + 5], cnt;
int phi[maxn + 5];
void Phi() {
	phi[1] = 1;
	vis[1] = true;
	for (int i = 2; i <= maxn; i++) {
		if (!vis[i]) prime[cnt++] = i, phi[i] = i - 1;
		for (int j = 0; j < cnt && prime[j] * i <= maxn; j++) {
			vis[prime[j] * i] = 1;
			if (i % prime[j] == 0) {
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * (prime[j] - 1);
		}
	}
}
int a[maxn], ops[maxn];
LL res[maxn];
struct Node {
	int id;
	int left;
	int right;
	bool operator <(const Node& a)const{
		if (ops[left] == ops[a.left])
			return right < a.right;
		return ops[left] < ops[a.left];
	}
} q[maxn];
LL num[maxn];
int main() {
	Init();
	Phi();
	int t, n, m, g = 0;
	cin >> t;
	while (t--) {
		printf("Case #%d:\n", ++g);
		scanf("%d", &n);
		int Size = (int)sqrt(n * 1.0);
		for (int i = 1; i <= n; i++)scanf("%d", &a[i]);
		for (int i = 1; i <= n; i++)ops[i] = i / Size;
		scanf("%d", &m);
		for (int i = 1; i <= m; i++){
			scanf("%d%d", &q[i].left, &q[i].right);
			q[i].id = i;
		}
		sort(q + 1, q + 1 + m);
		int stdl = 1, stdr = 0;
		LL ans = 0; int d;
		for (int i = 1; i <= m; i++){
			while (stdl > q[i].left){
				stdl--;
				for (int j = 1; j <= E[a[stdl]][0]; j++) {
					d = E[a[stdl]][j];
					num[d]++;
					ans += (num[d] - 1) * phi[d];
				}
			}
			while (stdr < q[i].right){
				stdr++;
				for (int j = 1; j <= E[a[stdr]][0]; j++) {
					d = E[a[stdr]][j];
					num[d]++;
					ans += (num[d] - 1) * phi[d];
				}
			}
			while (stdl < q[i].left){
				for (int j = 1; j <= E[a[stdl]][0]; j++) {
					d = E[a[stdl]][j];
					ans -= (num[d] - 1) * phi[d];
					num[d]--;
				}
				stdl++;
			}
			while (stdr > q[i].right){
				for (int j = 1; j <= E[a[stdr]][0]; j++) {
					d = E[a[stdr]][j];
					ans -= (num[d] - 1) * phi[d];
					num[d]--;
				}
				stdr--;
			}
			res[q[i].id] = ans;
		}
		for (int i = 1; i <= m; i++)
			printf("%lld\n", res[i]);
		memset(num, 0, sizeof(num));
	}
} 
  Happy 2006代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
int Phi(int n) {
	int ans = n;
	for (int i = 2; i * i <= n; i++) {
		if (n % i == 0) {
			ans = ans / i * (i - 1);
			while (n % i == 0) n /= i;
		}
	}
	if (n > 1) ans = ans / n * (n - 1);
	return ans;
}
int gcd(int a, int b) {
	return b == 0 ? a : gcd(b, a % b);
}
int main() {
	int n, k, phi;
	while (~scanf("%d%d", &n, &k)) {
		phi = Phi(n);
		LL ans = LL(k - 1) / phi * n;
		k %= phi;
		if (k == 0)k = phi;
		for (int i = 1; i <= n; i++) {
			if (gcd(i, n) == 1)
				k--;
			if (k == 0) {
				ans += LL(i); 
				break;
			}
		}
		printf("%lld\n", ans);
	}
}
 
  Huge Mods代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long int LL;
int Phi(int n) {
	int ans = n;
	for (int i = 2; i * i <= n; i++) {
		if (n % i == 0) {
			ans = ans / i * (i - 1);
			while (n % i == 0) n /= i;
		}
	}
	if (n > 1) ans = ans / n * (n - 1);
	return ans;
}
int mod, k;
int a[30];
int quickpow(LL m, LL p, LL mod) {
	LL res = 1, f1 = 0, f2 = 0;
	while (p) {
		if (p & 1) {
			f1 |= (res * m >= mod || f2);
			res *= m; res %= mod;
		}
		f2 |= (m * m >= mod);
		m *= m; m %= mod;
		p >>= 1;
	}
	return res + f1 * mod;
}
int slove(int x, int mod) {
	if (x == k) return quickpow(a[x], 1, mod);
	return quickpow(a[x], slove(x + 1, Phi(mod)), mod);
}
int main() {
	int g = 0;
	while (cin >> mod) {
		if (mod == '#')break;
		cin >> k;
		for (int i = 1; i <= k; i++) cin >> a[i];
		printf("Case #%d: %d\n", ++g, slove(1, mod) % mod);
	}
} 
  Calculation代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long int LL;
LL Phi(LL n) {
	LL ans = n;
	for (int i = 2; i * i <= n; i++) {
		if (n % i == 0) {
			ans = ans / i * (i - 1);
			while (n % i == 0) n /= i;
		}
	}
	if (n > 1) ans = ans / n * (n - 1);
	return ans;
}
LL quickpow(LL m, LL p, LL mod) {
	LL res = 1, f1 = 0, f2 = 0;
	while (p) {
		if (p & 1) {
			f1 |= (res * m >= mod || f2);
			res *= m; res %= mod;
		}
		f2 |= (m * m >= mod);
		m *= m; m %= mod;
		p >>= 1;
	}
	return res + f1 * mod;
}
LL n, m;
//f(n) = (n % 10) ^ f(n / 10)
LL slove(LL x, LL mod) {
	if (x == 0) return 1;
	return quickpow(x % 10, slove(x / 10, Phi(mod)), mod);
}
int main() {
	int t;
	scanf("%d", &t);
	while (t--) {
		scanf("%lld%lld", &n, &m);
		printf("%lld\n", slove(n, m) % m);
	}
} 
  Looooops代码 
  #include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL in2[35];
void Init() {
	for (int i = 1; i <= 34; i++)
		in2[i] = LL(1) << i;
}
LL gcd(LL a, LL b, LL& x, LL& y)
{
	if (b == 0) {
		x = 1, y = 0;
		return a;
	}
	int q = gcd(b, a % b, y, x);
	y -= a / b * x;
	return q;
}
int main() {
	Init();
	LL a, b, c, k;
	while (cin >> a >> b >> c >> k && a + b + c + k) {
		LL x, y;
		LL d = gcd(c, in2[k], x, y);
		if ((b - a) % d == 0) {
			LL ans = x * (b - a) / d % in2[k];
			printf("%lld\n", (ans % (in2[k] / d) + in2[k] / d) % (in2[k] / d));
		}
		else
			printf("FOREVER\n");
	}
} 
  青蛙的约会代码 
  #include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL in2[35];
void Init() {
	for (int i = 1; i <= 34; i++)
		in2[i] = LL(1) << i;
}
LL gcd(LL a, LL b, LL& x, LL& y)
{
	if (b == 0) {
		x = 1, y = 0;
		return a;
	}
	int q = gcd(b, a % b, y, x);
	y -= a / b * x;
	return q;
}
int main() {
	LL a, b, m, n, L, x, y;
	cin >> a >> b >> m >> n >> L;
	LL c = a - b; 
	a = n - m;
	LL d = gcd(a, L, x, y);
	if (c % d == 0) {
		LL ans = x * c / d;
		ans %= (L / d);
		if (ans < 0)ans += L / d;
		printf("%lld\n", ans);
	}
	else
		printf("Impossible\n");
} 
  A Modular Arithmetic Challenge代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL slove(LL M, LL D, LL L, LL R) {
	if (L > R || D == 0) return -1;
	if (R / D * D >= L) return (L + D - 1) / D;
	LL l = (-L) % D; if (l < 0) l += D;
	LL r = (-R) % D; if (r < 0) r += D;
	LL x = slove(D, M % D, r, l);
	if (x == -1)return -1;
	return (L + x * M + D - 1) / D;
}
int main() {
	LL D, M, L, R, t;
	cin >> t;
	while (t--) {
		cin >> M >> D >> L >> R;
		R = min(M - 1, R);
		cout << slove(M, D, L, R) << '\n';
	}
} 
  Strange Way to Express Integers代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL gcd(LL a, LL b, LL& x, LL& y)
{
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	LL q = gcd(b, a % b, y, x);
	y -= a / b * x;
	return q;
}
int main() {
	LL k, m1, m2, a1, a2, x, y, c;
	while (~scanf("%lld", &k)) {
		scanf("%lld%lld", &m1, &a1);
		bool flag = true;
		k--;
		while (k--) {
			scanf("%lld%lld", &m2, &a2);
			c = gcd(m1, m2, x, y);
			if ((a2 - a1) % c) flag = false;
			if(flag){
				x = (a2 - a1) / c * x;
				y = m2 / c;
				x = (x % y + y) % y;
				a1 = x * m1 + a1;
				m1 = (m1 * m2) / c;
			}
		}
		c = gcd(1, m1, x, y);
		if (a1 % c) flag = false;
		if(!flag) printf("-1\n");
		else {
			x = a1 / c * x;
			y = m1 / c;
			x = (x % y + y) % y;
			printf("%lld\n", x);
		}
	}
} 
  GCD Table代码 
  #include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL gcd(LL a, LL b) {
	return b == 0 ? a : gcd(b, a % b);
}
LL lcm(LL a, LL b) {
	return a / gcd(a, b) * b;
}
LL exgcd(LL a, LL b, LL& x, LL& y) {
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	LL q = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return q;
}
LL mul(LL x, LL p, LL mod) {
	if (p < 0) x = -x, p = -p;
	LL ret = 0;
	for (; p; p >>= 1, x = (x + x) % mod) if (p & 1) ret = (ret + x) % mod;
	return ret;
}
LL _x, _y, k;
LL m[10005], a[10005];
LL CRT() {
	LL m1, m2, a1, a2, x, y, c;
	m1 = m[1];
	a1 = a[1];
	bool flag = true;
	for (int i = 2; i <= k; i++) {
		m2 = m[i];
		a2 = a[i];
		c = exgcd(m1, m2, x, y);
		if ((a2 - a1) % c)
			flag = false;
		y = m2 / c;
		x = mul((a2 - a1) / c, x, y);
		x = (x % y + y) % y;
		a1 = x * m1 + a1;
		m1 = (m1 * m2) / c;
	}
	c = exgcd(1, m1, x, y);
	if (a1 % c) flag = false;
	if (!flag)
		return -1;
	x = a1 / c * x;
	y = m1 / c;
	x = (x % y + y) % y;
	return x == 0 ? y : x;
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> _x >> _y >> k;
	LL Lcm = 1;
	for (int i = 1; i <= k; i++) {
		cin >> m[i];
		Lcm = lcm(Lcm, m[i]);
		if (Lcm > _x) {
			printf("NO\n");
			return 0;
		}
		a[i] = ((m[i] - i + 1) % m[i] + m[i]) % m[i];
	}
	LL ans = CRT();
	if (ans == -1 || ans + k - 1 > _y) {
		printf("NO\n");
		return 0;
	}
	for (int i = 1; i <= k; i++) {
		if (gcd(Lcm, ans + i - 1) != m[i]) {
			printf("NO\n");
			return 0;
		}
	}
	printf("YES\n");
} 
   [SDOI2011]计算器代码 
  #include 
#include 
#include 
#include 
using namespace std;
#pragma warning (disable:4996)
typedef long long LL;
LL quickpow(LL m, LL p, LL mod) {
	LL res = 1;
	while (p) {
		if (p & 1) {
			res *= m;
			res %= mod;
		}
		m *= m;
		m %= mod;
		p >>= 1;
	}
	return res;
}
LL exgcd(LL a, LL b, LL& x, LL& y)
{
	if (b == 0) {
		x = 1, y = 0;
		return a;
	}
	LL q = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return q;
}
LL bsgs(LL a, LL b, LL p) {
	map H;
	H.clear();
	b %= p;
	LL t = (LL)sqrt(p) + 1;
	for (int i = 0; i < t; i++) {
		LL val = (LL)b * quickpow(a, i, p) % p;
		H[val] = i;
	}
	a = quickpow(a, t, p);
	if (!a) return b ? -1 : 1;
	for (int i = 0; i <= t; i++) {
		LL val = quickpow(a, i, p);
		LL j = H.find(val) == H.end() ? -1 : H[val];
		if (j >= 0 && i * t >= j) return i * t - j;
	}
	return -1;
}
int main() {
	LL t, k, _y, _z, _p, x, y;
	while (~scanf("%lld%lld", &t, &k)) {
		while (t--) {
			scanf("%lld%lld%lld", &_y, &_z, &_p);
			if (k == 1) {
				printf("%lld\n",quickpow(_y, _z, _p) % _p);
			}
			else if (k == 2) {
				LL a = _y, b = _p, d;
				d = exgcd(a, b, x, y);
				if (_z % d) {
					printf("Orz, I cannot find x!\n");
					continue;
				}
				x = _z / d * x;
				y = _p / d;
				x %= y; if (x < 0)x += y;
				printf("%lld\n", x);
			}
			else {
				LL ans = bsgs(_y, _z, _p);
				if (ans == -1) {
					printf("Orz, I cannot find x!\n");
					continue;
				}
				printf("%lld\n", ans);
			}
		}
	}
}

致良知之寄诸用明书 BonSun
众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
Python【math数学函数】 Alan_Lowe #Python python
Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
python 实现eulers totient欧拉方程算法 luthane 算法 python 开发语言
eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
算法设计与分析学习（6）——数论罗塞菈桔梨萝柚算法学习算法线性代数
数论整除基本概念若aaa和bbb为整数，且a≠0a≠0a=0若存在整数qqq使得b=aqb=aqb=aq，那么就说aaa可以整除bbb或是bbb被aaa整除，记作a∣ba|ba∣b。aaa也被称为bbb的约数，bbb也被称为a的倍数。若bbb不能被aaa整除，则记作a∤ba\not{|}ba∣b。整数p≠0,±1p≠0,±1p=0,±1，且除了±1,±p±1,±p±1,±p外没有其他的约数
数论——欧几里得算法 NarutoTime 数论算法 c++数据结构 c语言
1.欧几里得简介欧几里得（希腊文：Ευκλειδης，约公元前330年—公元前275年），古希腊数学家，被称为“几何之父”。他最著名的著作《几何原本》是欧洲数学的基础，在书中他提出五大公设。欧几里得的《几何原本》被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。2.欧几里得算法欧几里得算法用于：求解a和b的最大公约数。最大公约数英文为：Gre
数论——扩展欧几里得算法 NOI_yzk
欧几里得&拓展欧几里得（Euclid&Extend-Euclid）欧几里得算法（Euclid）背景：欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。——百度百科代码：递推的代码是相当的简洁：intgcd(inta,intb){returnb==0?a:gcd(b,a%b);}分析：方法说了是辗转相除法，自然没有什么好介绍的了。。Fresh肯定会觉得这样递归下去会不会爆栈？实际上在
数论学习1（欧几里德算法+唯一分解定理+埃氏筛+拓展欧几里德+同余与模算术） new出新对象！数学数算法学习
目录1.唯一分解定理2.欧几里德算法（求最大公约数）3.求最小公倍数4.埃氏筛5.拓展欧几里德算法(1)证明一下线性方程组的正数的最小值是多少，(2)如何通过裴蜀定理退出拓展欧几里得算法(贝祖定理)6.同余与模算术(1)取模运算操作加法取模运算减法取模运算乘法取模运算(2)特殊的取模操作大整数取模幂取模(3)同余式，乘法逆元，费马小定理今天也是小小的开始学习数论方面的知识了，首先数论的入门章节必然
Collatz 猜想和 Python 不连续小姐
PythonDay4:CollatzConjecture原来总有学生问我，微积分有什么用啊，我说如果微积分学好了，也许抽象代数和数论就能学好，那最后就能像AndrewWiles一样上人物年度杂志的封面了.(AndrewWiles证明了Fermat'sLastTheorem，费玛大定理).[captionid="attachment_1466"align="alignnone"width="300"
初等数论--整除--带余除法 WeidanJi 初等数论数学密码学信息安全
初等数论--整除--带余除法概念基本性质带余除法博主本人是初学初等数论（整除+同余+原根），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。我整理成一个系列：初等数论，方便检索。概念初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。初等数论研究对象是整数集合和自然数集合。b∣a:若a,b∈Z,b≠0，∃c∈Z,使a=bc,则称b整除a
河南萌新2024第四场 Pown_ShanYu 算法数据结构
C岗位分配题目大意：有n个岗位，m位志愿者，每个岗位至少需要a个志愿者，并且可以有志愿者可以空闲下来作预备，给出可能的分配情况总数思路：首先将每个岗位分配好至少需要的志愿者，再将剩下的人进行分配，那就满足球同盒不同模型（允许空盒），可用隔板法进行分配，需要额外开设一个空闲岗位用来预备，那么按照4个人去4个岗位，那么为c73，具体操作可看数论模板中发布的隔板法问题，递归求组合数Solved：intn
【读书笔记】吴非《致青年教师》(4) 冬儿菇凉
一、精要摘录(48——106页)1.教育教学不能“唯分数论“，比分数重要的是学生思维品质和解决实际问题的能力。2.一名教师心中有使命感，心中有学生才会很在意学生对他的态度，在意学生的接受度。3.作为教师，你要善于向学生问出有意思的问题。4.教育就是要培养好习惯，教是为了达到不需要教学生，不需要老师教了是教学的成功，也是教师的职业追求。5.教师是学习者，在学习上教师首先要郑重其事，学生才有可能养成敬
【代码随想录算法训练营Day39】62.不同路径；63. 不同路径 II 想做一只潜水的猪算法
文章目录❇️Day39第九章动态规划part02✴️今日任务❇️62.不同路径自己的思路自己的代码随想录思路随想录代码❇️63.不同路径II自己的思路自己的代码随想录代码❇️Day39第九章动态规划part02✴️今日任务今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径63.不同路径II❇️62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难
算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II memolaner 算法训练营算法动态规划数据结构 c++python
今天开始逐渐有dp的感觉了，题目不多，就两个不同路径，可以好好研究一下62.不同路径本题大家掌握动态规划的方法就可以。数论方法有点非主流，很难想到。代码随想录视频讲解：动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili这个题看到路径的表示，第一直觉就是一个组合数的问题，学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成，重点是把二维的动态规划
牛客周赛 Round 35（A,B,C,D,E,F,G）邪神与厨二病牛客算法暴力 c++数论滑动窗口单调队列贪心构造
这场简单，甚至赛时90分钟不到就AK了。比赛链接，队友题解友链刚入住学校监狱，很不适应，最近难受的要死，加上最近几场CF打的都不顺利，san值要爆掉了，只能慢慢补题了。这场C是个滑动窗口，D是贪心，E是有点麻烦的构造，FG是数论。A小红的字符串切割思路：记录一下字符串长度，然后从中间拆开。code：#include#include#includeusingnamespacestd;strings;
算法——数论——同余戏拈秃笔数据结构与算法（java版）算法
目录同余一、试题算法训练同余方程同余同余使人们能够用等式的形式简洁地描述整除关系同余：若m（正整数），a和b是整数，a%m==b%m，或(a-b)%m==0，记为ab(modm)求解一元线性同余方程等价于求解二元线性丢番图方程一元线性同余方程，解法看下面第一题二元线性丢番图方程逆：的一个解为a模m的逆一、试题算法训练同余方程问题描述求关于x的同余方程ax≡1(modb)的最小正整数解。输入格式输入
pku acm 题目分类 moxiaomomo 算法数据结构 numbers 优化 calendar combinations
1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
C++STL之Queue容器芯片烧毁大师数据结构 C++c++开发语言
C++STL之Queue容器1.再谈队列回顾一下之前所学的队列，队列和栈不同，队列是一种先进先出的数据结构，STL的队列内容极其重要，虽然内容较少但是请务必掌握，STL的队列是快速构建搜索算法以及相关的数论图论的状态存储的基础。2.相关头文件头文件：#include3.初始化格式为：**explicit**queue(**const**container_type&ctnr=container_t
数字签名算法MD5withRSA Just_Paranoid 技术流Clip md5 rsa signatrue
数字签名MD5withRSA，：将正文通过MD5数字摘要后，将密文再次通过生成的RSA密钥加密，生成数字签名，将明文与密文以及公钥发送给对方，对方拿到私钥/公钥对数字签名进行解密，然后解密后的，与明文经过MD5加密进行比较，如果一致则通过使用Signature的API来实现MD5withRSARSA原理：RSA算法基于一个十分简单的数论事实，将两个大素数相乘十分容易，但反过来想要对其乘积进行因式分
2301: 不定方程解的个数 jht0105 算法
题目描述输出不定方程解的个数。在数学中，不定方程是数论中的一个重要课题，在各种比赛中也常常出现.对于不定方程，有时我们往往只求非负整数解，现有方程ax+by+c=0，其中x、y为未知量且不超过10000，当给定a、b、c的值以后，可求出n组x、y的非负整数解，n>=0，,其中a，b，c均为[-10000,10000].输入描述一行，三个空格隔开的整数，为a、b、c的值。输出描述一个整数，为合法的解
python伯努利多项式微小冷 #sympy python 开发语言 sympy 伯努利数排列组合符号计算
文章目录伯努利数和多项式sympy实现伯努利数是一种在数学、物理和工程中广泛应用的特殊数列，以瑞士数学家雅各布·伯努利（JacobBernoulli）的名字命名，并在许多领域中发挥重要作用。在数学中，它们与斐波那契数列、卡塔兰数、贝尔数等数列有密切联系，可以用于解决循环问题、组合问题和递推关系等数学问题。伯努利数和多项式伯努利(Bernoulli)数是一组在数论和复分析中出现的数，与伯努利多项式有
二次剩余问题x的求解及代码实现（python） JustGo12 数论安全 1024程序员节
一、问题引入二次剩余是数论基本概念之一。它是初等数论中非常重要的结果，不仅可用来判断二次同余式是否有解，还有很多用途。C.F.高斯称它为算术中的宝石，他一人先后给出多个证明。[1]研究二次剩余的理论称为二次剩余理论。二次剩余理论在实际上有广泛的应用，包括从噪音工程学到密码学以及大数分解。即关于方x^2≡a(modp)对于这个方程，求出满足条件的x。二、x的求解在上述问题下，根据p值的不同性质，可以
【数论】exgcd 扩展欧几里得算法 Texcavator 数论算法
参考：exgcd详解-zzt1208-博客园(cnblogs.com)exgcd（扩展欧几里得算法），用来求形如ax+by=gcd(a,b)ax+by=gcd(a,b)ax+by=gcd(a,b)（a,ba,ba,b为常数）的方程的一组整数解。（如果不确定等号右边是不是gcd，可以先当做gcd，求出来之后验证，是的话就是解，不是的话就不是解）推导见上面的链接，这篇只放个板子codeintexgcd
2021-07-30 RX-0493
学了一会数论，好难1.乘法逆元：a/b%p,若a/b在进行取模运算时，会出现精度问题，而且模运算对除法不适用，（没有分配律，大概就这意思）而求出乘法逆元后，可以把原式变为a*x%p的形式，且值不变。a*x≡1（modp）中，a,p为已知量，则x为a的乘法逆元。例题：乘法逆元设p=k*i+r,(1usingnamespacestd;constintN=20000530;intn,p,inv[N];i
同余数论性质 clmm_ 算法
同余概念当a%m==b%m，说明a和b同余，写作若a≡b(modm)性质衍生出几条性质1.m|abs(a-b)，即|a-b|是m的倍数。（注意，0是任何数的倍数）2.当a≡b(modm)，c≡d(modm)，有ac≡bd(modm)有a+c≡b+d(modm)有a-c≡b-d(modm)证明如下
读《爱心与教育》第八天皮_小皮
作为一名教师，尤其是班主任老师，“培优转差”是教育工作的一项重要内容，读了李镇西老师的《爱心与教育》，自己受到不小的启发，对“优生”的培养和后进生的转化有了新的认识和思考。对“优生”的重新认识——李老师说：“优生”当然应该是指品学兼优的学生，但在现在不少教师、家长的眼中，所谓“优生”更多的是指学习成绩拔尖的学生（即尖子生）。的确，在升学竞争和应试教育的大环境下，很多教育者都以分数论英雄，对“优生”
RSA算法 superdont 图像加密算法 java 服务器
RSA算法是一个非对称加密算法，它依赖于数论中的大整数因数分解问题的困难性。在RSA中，加密和解密使用不同的密钥，分别称为公钥和私钥。RSA算法的基本原理包括以下几个步骤：密钥生成：a.选择两个大的质数(p)和(q)。b.计算它们的乘积(n=pq)，n的长度就是密钥长度。c.计算欧拉函数(\phi(n)=(p-1)(q-1))。d.选择一个整数(e)，使得(1
日精进110天金八力韩英雪
敬爱的老师，智慧的班主任，亲爱的跃友们：大家好！我是来自山峰教外教育的韩英雪，今天是我的日精进行动第110天，给大家分享我今天的进步，我们互相勉励，携手前行。每天进步一点点，距离成功便不远。1、比学习:个体身心发展的规律。顺序性，阶段性，不平衡性，互补性，个别差异性和整体性。个体身心发展的能动动因主要由内发论，外数论多因素互相作用论。其中内发论的代表人物包括孟子，弗洛伊德，威尔逊，格赛尔，霍尔等外
[C语言]Day04作业：输出菱形,判断水仙花数,输出a = aaaaa MrDorli C语言学习 c语言
/*1.在屏幕上输出以下图案：*************************************************************************************2.求出0～999之间的所有“水仙花数”并输出。“水仙花数”是指一个三位数，其各位数字的立方和确好等于该数本身，如；153＝1＋5＋3?，则153是一个“水仙花数”。在数论中，水仙花数（Narciss
信安数基2-同余方程利賀田
基本概念及一次同余式同余式是数论的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m|(a-b)，则称a与b对模m同余，记为a≡b(modm)，或记为a≡b(m)。这个式子称为模m的同余式，若m∤(a-b)，则称a、b对模m不同余，同余概念又常表达为：1.a=b+km(k∈Z)；2.a和b被m除时有相同的[余数]。同余式的记号由高斯(Gauss,C.F.)于1800年首创,发表在他的数论
【数论】矩阵快速幂 Texcavator 数论矩阵算法数据结构
参考：P3193[HNOI2008]GT考试题解放个板子structMartix{inta[30][30];//在这里修改矩阵的大小Martix(){memset(a,0,sizeof(a));}Martixoperator*(constMartix&B)const//乘法运算符重载{Martixres;for(inti=0;i>=1;a=a*a;}returnans;}
JAVA基础灵静志远位运算加载 Date 字符串池覆盖
一、类的初始化顺序 1 （静态变量，静态代码块）-->（变量，初始化块）--> 构造器同一括号里的，根据它们在程序中的顺序来决定。上面所述是同一类中。如果是继承的情况，那就在父类到子类交替初始化。二、String 1 String a = "abc"; JAVA虚拟机首先在字符串池中查找是否已经存在了值为"abc"的对象，根
keepalived实现redis主从高可用 bylijinnan redis
方案说明两台机器（称为A和B），以统一的VIP对外提供服务 1.正常情况下，A和B都启动，B会把A的数据同步过来（B is slave of A） 2.当A挂了后，VIP漂移到B；B的keepalived 通知redis 执行：slaveof no one，由B提供服务 3.当A起来后，VIP不切换，仍在B上面；而A的keepalived 通知redis 执行slaveof B，开始
java文件操作大全 0624chenhong java
最近在博客园看到一篇比较全面的文件操作文章，转过来留着。 http://www.cnblogs.com/zhuocheng/archive/2011/12/12/2285290.html 转自http://blog.sina.com.cn/s/blog_4a9f789a0100ik3p.html 一.获得控制台用户输入的信息 &nbs
android学习任务不懂事的小屁孩工作
任务完成情况搞清楚带箭头的pupupwindows和不带的使用已完成熟练使用pupupwindows和alertdialog，并搞清楚两者的区别已完成熟练使用android的线程handler,并敲示例代码进行中了解游戏2048的流程，并完成其代码工作进行中-差几个actionbar 研究一下android的动画效果，写一个实例已完成复习fragem
zoom.js 换个号韩国红果果 oom
它的基于bootstrap 的 https://raw.github.com/twbs/bootstrap/master/js/transition.js transition.js模块引用顺序 <link rel="stylesheet" href="style/zoom.css"> <script src=&q
详解Oracle云操作系统Solaris 11.2 蓝儿唯美 Solaris
当Oracle发布Solaris 11时，它将自己的操作系统称为第一个面向云的操作系统。Oracle在发布Solaris 11.2时继续它以云为中心的基调。但是，这些说法没有告诉我们为什么Solaris是配得上云的。幸好，我们不需要等太久。Solaris11.2有4个重要的技术可以在一个有效的云实现中发挥重要作用：OpenStack、内核域、统一存档（UA）和弹性虚拟交换（EVS）。
spring学习——springmvc（一） a-john springMVC
Spring MVC基于模型-视图-控制器（Model-View-Controller，MVC）实现，能够帮助我们构建像Spring框架那样灵活和松耦合的Web应用程序。 1，跟踪Spring MVC的请求请求的第一站是Spring的DispatcherServlet。与大多数基于Java的Web框架一样，Spring MVC所有的请求都会通过一个前端控制器Servlet。前
hdu4342 History repeat itself-------多校联合五 aijuans 数论
水题就不多说什么了。 #include<iostream>#include<cstdlib>#include<stdio.h>#define ll __int64using namespace std;int main(){ int t; ll n; scanf("%d",&t); while(t--)
EJB和javabean的区别 asia007 bean ejb
EJB不是一般的JavaBean,EJB是企业级JavaBean,EJB一共分为3种,实体Bean,消息Bean,会话Bean,书写EJB是需要遵循一定的规范的,具体规范你可以参考相关的资料.另外,要运行EJB,你需要相应的EJB容器,比如Weblogic,Jboss等,而JavaBean不需要,只需要安装Tomcat就可以了 1.EJB用于服务端应用开发, 而JavaBeans
Struts的action和Result总结百合不是茶 struts Action配置 Result配置
一:Action的配置详解: 下面是一个Struts中一个空的Struts.xml的配置文件 <?xml version="1.0" encoding="UTF-8" ?> <!DOCTYPE struts PUBLIC &quo
如何带好自已的团队 bijian1013 项目管理团队管理团队
在网上看到博客" 怎么才能让团队成员好好干活"的评论，觉得写的比较好。原文如下：我做团队管理有几年了吧，我和你分享一下我认为带好团队的几点： 1.诚信对团队内成员，无论是技术研究、交流、问题探讨，要尽可能的保持一种诚信的态度，用心去做好，你的团队会感觉得到。 2.努力提
Java代码混淆工具 sunjing ProGuard
Open Source Obfuscators ProGuard http://java-source.net/open-source/obfuscators/proguardProGuard is a free Java class file shrinker and obfuscator. It can detect and remove unused classes, fields, m
【Redis三】基于Redis sentinel的自动failover主从复制 bit1129 redis
在第二篇中使用2.8.17搭建了主从复制，但是它存在Master单点问题，为了解决这个问题，Redis从2.6开始引入sentinel，用于监控和管理Redis的主从复制环境，进行自动failover，即Master挂了后，sentinel自动从从服务器选出一个Master使主从复制集群仍然可以工作，如果Master醒来再次加入集群，只能以从服务器的形式工作。什么是Sentine
使用代理实现Hibernate Dao层自动事务白糖_ DAO spring AOP 框架 Hibernate
都说spring利用AOP实现自动事务处理机制非常好，但在只有hibernate这个框架情况下，我们开启session、管理事务就往往很麻烦。 public void save(Object obj){ Session session = this.getSession(); Transaction tran = session.beginTransaction(); try
maven3实战读书笔记 braveCS maven3
Maven简介是什么？ Is a software project management and comprehension tool.项目管理工具是基于POM概念(工程对象模型) [设计重复、编码重复、文档重复、构建重复，maven最大化消除了构建的重复] [与XP：简单、交流与反馈；测试驱动开发、十分钟构建、持续集成、富有信息的工作区] 功能：
编程之美-子数组的最大乘积 bylijinnan 编程之美
public class MaxProduct { /** * 编程之美子数组的最大乘积 * 题目: 给定一个长度为N的整数数组，只允许使用乘法，不能用除法，计算任意N-1个数的组合中乘积中最大的一组，并写出算法的时间复杂度。 * 以下程序对应书上两种方法，求得“乘积中最大的一组”的乘积——都是有溢出的可能的。 * 但按题目的意思，是要求得这个子数组，而不
读书笔记-2 chengxuyuancsdn 读书笔记
1、反射 2、oracle年-月-日时-分-秒 3、oracle创建有参、无参函数 4、oracle行转列 5、Struts2拦截器 6、Filter过滤器(web.xml) 1、反射 (1)检查类的结构在java.lang.reflect包里有3个类Field,Method,Constructor分别用于描述类的域、方法和构造器。 2、oracle年月日时分秒 s
[求学与房地产]慎重选择IT培训学校 comsci it
关于培训学校的教学和教师的问题,我们就不讨论了,我主要关心的是这个问题培训学校的教学楼和宿舍的环境和稳定性问题我们大家都知道，房子是一个比较昂贵的东西，特别是那种能够当教室的房子... &nb
RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系 daizj oracle rman filesperset PARALLELISM
RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系转 PARALLELISM --- 我们还可以通过parallelism参数来指定同时"自动"创建多少个通道： RMAN > configure device type disk parallelism 3 ; 表示启动三个通道，可以加快备份恢复的速度。
简单排序:冒泡排序 dieslrae 冒泡排序
public void bubbleSort(int[] array){ for(int i=1;i<array.length;i++){ for(int k=0;k<array.length-i;k++){ if(array[k] > array[k+1]){
初二上学期难记单词三 dcj3sjt126com sciet
concert 音乐会 tonight 今晚 famous 有名的；著名的 song 歌曲 thousand 千 accident 事故；灾难 careless 粗心的，大意的 break 折断；断裂；破碎 heart 心（脏） happen 偶尔发生，碰巧 tourist 旅游者；观光者 science （自然）科学 marry 结婚 subject 题目；
I.安装Memcahce 1. 安装依赖包libevent Memcache需要安装libevent,所以安装前可能需要执行 Shell代码收藏代码 dcj3sjt126com redis
wget http://download.redis.io/redis-stable.tar.gz tar xvzf redis-stable.tar.gz cd redis-stable make 前面3步应该没有问题，主要的问题是执行make的时候，出现了异常。异常一： make[2]: cc: Command not found 异常原因：没有安装g
并发容器 shuizhaosi888 并发容器
通过并发容器来改善同步容器的性能，同步容器将所有对容器状态的访问都串行化，来实现线程安全，这种方式严重降低并发性，当多个线程访问时，吞吐量严重降低。并发容器ConcurrentHashMap 替代同步基于散列的Map，通过Lock控制。 &nb
Spring Security（12）——Remember-Me功能 234390216 Spring Security Remember Me 记住我
Remember-Me功能目录 1.1 概述 1.2 基于简单加密token的方法 1.3 基于持久化token的方法 1.4 Remember-Me相关接口和实现
位运算焦志广位运算
一、位运算符Ｃ语言提供了六种位运算符： & 按位与 | 按位或 ^ 按位异或 ~ 取反 << 左移 >> 右移 1. 按位与运算按位与运算符"&"是双目运算符。其功能是参与运算的两数各对应的二进位相与。只有对应的两个二进位均为1时，结果位才为1 ，否则为0。参与运算的数以补码方式出现。例如：9&am
nodejs 数据库连接 mongodb mysql liguangsong mongodb mysql node 数据库连接
1.mysql 连接 package.json中dependencies加入 "mysql":"~2.7.0" 执行 npm install 在config 下创建文件 database.js
java动态编译 olive6615 java HotSpot jvm 动态编译
在HotSpot虚拟机中，有两个技术是至关重要的，即动态编译(Dynamic compilation)和Profiling。 HotSpot是如何动态编译Javad的bytecode呢？Java bytecode是以解释方式被load到虚拟机的。HotSpot里有一个运行监视器，即Profile Monitor,专门监视
Storm0.9.5的集群部署配置优化 roadrunners 优化 storm.yaml
nimbus结点配置（storm.yaml）信息： # Licensed to the Apache Software Foundation (ASF) under one # or more contributor license agreements. See the NOTICE file # distributed with this work for additional inf
101个MySQL 的调节和优化的提示 tomcat_oracle mysql
　1. 拥有足够的物理内存来把整个InnoDB文件加载到内存中——在内存中访问文件时的速度要比在硬盘中访问时快的多。　　2. 不惜一切代价避免使用Swap交换分区 – 交换时是从硬盘读取的，它的速度很慢。　　3. 使用电池供电的RAM（注：RAM即随机存储器）。　　4. 使用高级的RAID（注：Redundant Arrays of Inexpensive Disks，即磁盘阵列
zoj 3829 Known Notation(贪心) 阿尔萨斯 ZOJ
题目链接：zoj 3829 Known Notation 题目大意：给定一个不完整的后缀表达式，要求有2种不同操作，用尽量少的操作使得表达式完整。解题思路：贪心，数字的个数要要保证比∗的个数多1，不够的话优先补在开头是最优的。然后遍历一遍字符串，碰到数字+1，碰到∗-1,保证数字的个数大于等1，如果不够减的话，可以和最后面的一个数字交换位置（用栈维护十分方便），因为添加和交换代价都是1

ACM数论基础 详细整理

质数

质数的判定

试除法

MillerRobbin(米勒罗宾素数测试)

素数筛法

埃氏筛

线性筛

区间筛

Prime Distance

HDU6069 Counting Divisors（区间分解质因数）

阶乘分解

ural1055 Combinations

约数

算术基本定理的扩展

数值分块

BZOJ1257 余数之和

BZOJ2956 模积和

最大公约数

欧几里得算法

区间GCD

HDU 5726 GCD

HDU 5869 Different GCD Subarray Query

欧拉函数

POJ2478 Farey Sequence

POJ3090 Visible Lattice Points

POJ2480 Longge's problem

BZOJ 4804 欧拉心算 心酸

HDU5780 gcd

HDU4676 Sum Of Gcd

同余

同余类

剩余系

POJ2773 Happy 2006

欧拉定理

欧拉定理推论

UVA106992 Huge Mods

HDU2837 Calculation

裴蜀定理

扩展欧几里得算法

POJ2115 Looooops

POJ1061 青蛙的约会

同余不等式

POJ3530 A Modular Arithmetic Challenge

线性同余方程组

中国剩余定理

非互质线性同余方程组

POJ2891 Strange Way to Express Integers

GCD Table

高次同余方程

BSGS算法

bzoj2242 [SDOI2011]计算器

原根与指标

例题代码

Prime Distance 代码

Counting Divisors代码

Combinations代码

余数之和代码

模积和代码

斐波那契公约数代码

GCD代码

Different GCD Subarray Query代码

Farey Sequence代码

Visible Lattice Points代码

Longge's problem代码

欧拉心算 代码

gcd代码

Sum Of Gcd代码

Happy 2006代码

Huge Mods代码

Calculation代码

Looooops代码

青蛙的约会代码

A Modular Arithmetic Challenge代码

Strange Way to Express Integers代码

GCD Table代码

[SDOI2011]计算器代码

你可能感兴趣的:(数论)

ACM数论基础详细整理

BZOJ 4804 欧拉心算心酸

欧拉心算代码