【NOIP2017提高组正式赛】D2T3列队

Description

   Sylvia 是一个热爱学习的女孩子。
   前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。 Sylvia所在的方阵中有n × m名学生，方阵的行数为 n，列数为 m。
   为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中从 1 到 n × m 编上了号码（参见后面的样例）。即：初始时，第 i 行第 j 列的学生的编号是(i − 1) × m + j。
   然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了 q 件这样的离队事件。每一次离队事件可以用数对(y,z) (1≤x≤n,1≤y≤m)描述，表示第 x 行第 y 列的学生离队。
   在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：
   1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第 x 行第 m 列。
   2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第 n 行第 m 列。
   教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行第 m 列一个空位，这时这个学生会自然地填补到这个位置。
   因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学的编号是多少。

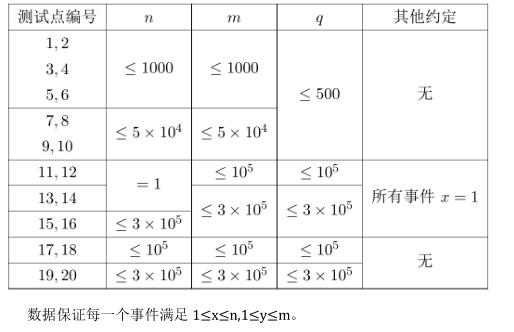
数据范围

题解

对于前面6个数据就直接暴力，
7、8、9、10，q都很小可以 O(q2) 的方法。
对于所有事件x=1这一部分，
修改的只有第一行，还有最后一列会修改，维护一棵线段树就可以了。
每次找第k大，然后在最加一个数。

其实这一部分的解法已经很接近正解了，
正解就是n+1棵线段树。
对于每一行，除去最后一个位置，建n棵线段树，
然后再对最后一列单独建一棵线段树，分别维护。
如果不在最后一列，
就先在对于那一行的线段树里面找到第k大的值，
并将这个点删掉，
再在最后一列里面找出对应的，加入到这一行里面，删掉这个位置。
最后将答案放到最后。

不能将所有点都保存下来，要动态开节点。

code

#include 
#include 
#include 
#include 
#include 
#define ll long long
#define N 300003
#define x_ (x<<1)
#define Mid ((l+r)>>1)
using namespace std;

struct node
{
    int l,r,s;
    ll w;
}t[60*N+5];

ll ans,g[N*4];
int tr[N*8],pos,f[N];
int n,m,q,xx,yy,tot,mx;
char ch;

void read(int& n)
{
    n=0;
    ll w=1;
    for(ch=getchar();(ch<'0' || ch>'9')&&(ch!='-');ch=getchar());
    if(ch=='-')w=-1,ch=getchar();
    for(;'0'<=ch && ch<='9';n=(n<<3)+(n<<1)+ch-48,ch=getchar());
    n=n*w;
}

void write(ll x)
{
    if(x>9)write(x/10);
    putchar(x%10+48);
}

void Kth(int x,int l,int r,int s)
{
    if(l==r)
    {
        ans=t[x].w;
        t[x].s=0;

        return;
    }
    if(!t[x].l)
    {
        t[x].l=++tot;
        t[tot].w=t[x].w;
        t[tot].s=t[x].s>Mid-l+1?Mid-l+1:t[x].s;
        t[x].r=++tot;
        t[tot].w=t[x].w+t[t[x].l].s;
        t[tot].s=t[x].s-t[t[x].l].s;
    }
    if(t[t[x].l].s<s)Kth(t[x].r,Mid+1,r,s-t[t[x].l].s);
        else Kth(t[x].l,l,Mid,s);
    t[x].s=t[t[x].l].s+t[t[x].r].s;
} 

void ins(int x,int l,int r,int z,ll y)
{
    if(l==r)
    {
        t[x].w=y;
        t[x].s=1;
        return;
    }
    if(!t[x].l)
    {
        t[x].l=++tot;
        t[tot].w=t[x].w;
        t[tot].s=t[x].s>Mid-l+1?Mid-l+1:t[x].s;
        t[x].r=++tot;
        t[tot].w=t[x].w+t[t[x].l].s;
        t[tot].s=t[x].s-t[t[x].l].s;
    }
    if(z<=Mid)ins(t[x].l,l,Mid,z,y);
        else ins(t[x].r,Mid+1,r,z,y);
    t[x].s=t[t[x].l].s+t[t[x].r].s;
}

int find(int x,int l,int r,int s)
{
    if(l==r)return l;
    if(tr[x_]<s)return find(x_+1,Mid+1,r,s-tr[x_]);
        else return find(x_,l,Mid,s);
}

void del(int x,int l,int r,int s)
{
    if(l==r)
    {
        tr[x]=0;
        return;
    }
    if(Mid<s)del(x_+1,Mid+1,r,s);
        else del(x_,l,Mid,s);
    tr[x]=tr[x_]+tr[x_+1];
}

void add(int x,int l,int r,int s)
{
    if(l==r)
    {
        tr[x]=1;
        return;
    }
    if(Mid<s)add(x_+1,Mid+1,r,s);
        else add(x_,l,Mid,s);
    tr[x]=tr[x_]+tr[x_+1];
}

void build(int x,int l,int r)
{
    if(l>n)return;
    if(l==r)
    {
        tr[x]=1;
        return;
    }
    build(x_,l,Mid);
    build(x_+1,Mid+1,r);
    tr[x]=tr[x_]+tr[x_+1];
}

int main()
{
    freopen("phalanx.in","r",stdin);
    freopen("phalanx.out","w",stdout);
    read(n);read(m);read(q);
    mx=(n>m?n:m)+q;
    for(ll i=1;i<=n;i++)
        t[i].w=(i-1)*m+1,t[i].s=m-1,g[i]=i*m;

    tot=n;
    build(1,1,mx);

    for(int i=1;i<=q;i++)
    {
        read(xx);read(yy);
        pos=find(1,1,mx,xx);
        if(yy!=m)f[xx]++,Kth(xx,1,mx,yy),
            ins(xx,1,mx,m+f[xx]-1,g[pos]);
            else ans=g[pos];


        del(1,1,mx,pos);
        add(1,1,mx,n+i);
        g[n+i]=ans;

        write(ans),putchar('\n');
    }
    return 0;
}