C++算法篇 递归调用(函数调用自身)
要理解运用递归要学习理解下面几个问题:
什么是递归?
递归的精髓(思想)是什么?
递归和循环的区别是什么?
什么时候该用递归?
使用递归需要注意哪些问题?
递归思想解决的几个经典的问题?
1、递归概念:
德罗斯特效应就是说,你拿着一面镜子,然后再站在一面镜子前面,让两面镜子相对。你看到镜子里面的情景,是相同的,无限循环的。
在数学与计算机科学中,递归是指在函数的定义中调用函数自身的方法。实际上递归其包含了两个意思:递 和 归,这正是递归思想的精华所在。
大师 L. Peter Deutsch 说过:人理解迭代,神理解递归。毋庸置疑地,递归确实是一个奇妙的思维方式。对一些简单的递归问题,我们总是惊叹于递归描述问题的能力和编写代码的简洁,但要想真正领悟递归的精髓、灵活地运用递归思想来解决问题却并不是一件容易的事情。在正式介绍递归之前,我们首先引用知乎用户李继刚对递归和循环的生动解释:
递归:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开它。若干次之后,你打开面前的门后,发现只有一间屋子,没有门了。然后,你开始原路返回,每走回一间屋子,你数一次,走到入口的时候,你可以回答出你到底用这你把钥匙打开了几扇门。
循环:你打开面前这扇门,看到屋里面还有一扇门。你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门(若前面两扇门都一样,那么这扇门和前两扇门也一样;如果第二扇门比第一扇门小,那么这扇门也比第二扇门小,你继续打开这扇门,一直这样继续下去直到打开所有的门。但是,入口处的人始终等不到你回去告诉他答案。
2、递归思想的精髓
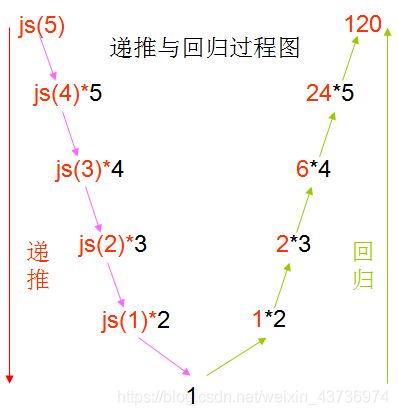
正如上面所描述的场景,递归就是有去(递去)有回(归来),如下图所示。“有去”是指:递归问题必须可以分解为若干个规模较小,与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决,就像上面例子中的钥匙可以打开后面所有门上的锁一样;“有回”是指 : 这些问题的演化过程是一个从大到小,由近及远的过程,并且会有一个明确的终点(临界点),一旦到达了这个临界点,就不用再往更小、更远的地方走下去。最后,从这个临界点开始,原路返回到原点,原问题解决。
更直接地说,递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。特别地,在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况,这也正是递归的定义所在。格外重要的是,这个解决问题的函数必须有明确的结束条件,否则就会导致无限递归的情况。
例题分析:求n!
#include
using namespace std;
int f(int n)
{ int m;
if (n==1) m=1;
else m=f(n-1)*n;
return m;
}
int main()
{ int x,y;
cin>>x;
y=f(x);
cout< 看程序写结果:
#include
using namespace std;
int f(int n)
{ int m;
if (n==1) m=10; //递归终止条件
else //先测试,后递归调用。
m=f(n-1)+2; //递归调用语句,该语句的参数应该逐渐逼近终止条件
return m;
}
int main()
{ int x=10,y;
y=f(x);
cout< 输出:
#include
using namespace std;
int f(int n)
{ if (n==1) return 1;
return n+f(n/2);
}
int main()
{ cout< 输出:
#include
using namespace std;
main()
{ int f(int);
int n,s;
n=10;
s=f(n);
printf("s=%d\n",s);
}
f(int x)
{ if(x==1) return 1;
else return(x+f(x-1));
}
输出:
3、递归的条件:
在我们了解了递归的基本思想及其数学模型之后,我们如何才能写出一个漂亮的递归程序呢?主要是把握好如下三个方面:
1). 明确递归终止条件
我们知道,递归就是有去有回,既然这样,那么必然应该有一个明确的临界点,程序一旦到达了这个临界点,就不用继续往下递去而是开始实实在在的归来。换句话说,该临界点就是一种简单情境,可以防止无限递归。
2). 给出递归终止时的处理办法
我们刚刚说到,在递归的临界点存在一种简单情境,在这种简单情境下,我们应该直接给出问题的解决方案。一般地,在这种情境下,问题的解决方案是直观的、容易的。
3). 提取重复的逻辑,缩小问题规模
我们在阐述递归思想内涵时谈到,递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决。从程序实现的角度而言,我们需要抽象出一个干净利落的重复的逻辑,以便使用相同的方式解决子问题。
4、递归算法的编程模型
在我们明确递归算法设计三要素后,接下来就需要着手开始编写具体的算法了。在编写算法时,不失一般性,我们给出两种典型的递归算法设计模型,如下所示。
模型一: 在递去的过程中解决问题
function recursion(大规模)
{ if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ // 在将问题转换为子问题的每一步,解决该步中剩余部分的问题
solve; // 递去
recursion(小规模); // 递到最深处后,不断地归来
}
}模型二: 在归来的过程中解决问题
function recursion(大规模)
{ if (end_condition){ // 明确的递归终止条件
end; // 简单情景
}else{ // 先将问题全部描述展开,再由尽头“返回”依次解决每步中剩余部分的问题
recursion(小规模); // 递去
solve; // 归来
}
}5. 递归与循环
递归与循环是两种不同的解决问题的典型思路。递归通常很直白地描述了一个问题的求解过程,因此也是最容易被想到解决方式。循环其实和递归具有相同的特性,即做重复任务,但有时使用循环的算法并不会那么清晰地描述解决问题步骤。单从算法设计上看,递归和循环并无优劣之别。然而,在实际开发中,因为函数调用的开销,递归常常会带来性能问题,特别是在求解规模不确定的情况下;而循环因为没有函数调用开销,所以效率会比递归高。递归求解方式和循环求解方式往往可以互换,也就是说,如果用到递归的地方可以很方便使用循环替换,而不影响程序的阅读,那么替换成循环往往是好的。问题的递归实现转换成非递归实现一般需要两步工作:
(1). 自己建立“堆栈(一些局部变量)”来保存这些内容以便代替系统栈,比如树的三种非递归遍历方式;
(2). 把对递归的调用转变为对循环处理。
特别地,在下文中我们将给出递归算法的一些经典应用案例,对于这些案例的实现,我们一般会给出递归和非递归两种解决方案,以便读者体会。
6、递归的应用场景
在我们实际学习工作中,递归算法一般用于解决三类问题:
(1). 问题的定义是按递归定义的(Fibonacci函数,阶乘,…);
(2). 问题的解法是递归的(有些问题只能使用递归方法来解决,例如,汉诺塔问题,…);
(3). 数据结构是递归的(链表、树等的操作,包括树的遍历,树的深度,…)。
下面我们将给出递归算法的一些经典应用案例。
1、第一类问题:问题的定义是按递归定义的
(1)阶乘
//递归解法
long f(int n)
{ if(n == 1) // 递归终止条件
return 1; // 简单情景
return n*f(n-1); // 相同重复逻辑,缩小问题的规模
}//非递归解法
long f_loop(int n)
{ long result = n;
while (n > 1)
{ n--;
result = result * n;
}
return result;
}(2)斐波纳契数列
//非递归解法
int fibonacci(int n)
{ if (n == 1 || n == 2) // 递归终止条件
return 1; // 简单情景
return fibonacci(n - 1) + fibonacci(n - 2); // 相同重复逻辑,缩小问题的规模
}
2、第二类问题:问题解法按递归算法实现
汉诺塔问题
moveDish(int level, char from, char inter, char to)
{ if (level == 1) // 递归终止条件
System.out.println("从" + from + " 移动盘子" + level + " 号到" + to);
else // 递归调用:将level-1个盘子从from移到inter(不是一次性移动,每次只能移动一个盘子,其中to用于周转)
{ moveDish(level - 1, from, to, inter); // 递归调用,缩小问题的规模
// 将第level个盘子从A座移到C座
System.out.println("从" + from + " 移动盘子" + level + " 号到" + to);
// 递归调用:将level-1个盘子从inter移到to,from 用于周转
moveDish(level - 1, inter, from, to); // 递归调用,缩小问题的规模
}
}
main(String[] args)
{ int nDisks = 30;
moveDish(nDisks, 'A', 'B', 'C');
}3、第三类问题:数据的结构是按递归定义的
(1)二叉树深度
//返回二叉数的深度
int getTreeDepth(Tree t)
{ //
if (t == null) // 树为空,递归终止条件
return 0;
int left = getTreeDepth(t.left); // 递归求左子树深度,缩小问题的规模
int right = getTreeDepth(t.left); // 递归求右子树深度,缩小问题的规模
return left > right ? left + 1 : right + 1;
}(2)二叉树前序遍历
String preOrder(Node root)
{ StringBuilder sb = new StringBuilder(); // 存到递归调用栈
if (root == null) // 递归终止条件
return ""; // ji
else // 递归终止条件
{
sb.append(root.data + " "); // 前序遍历当前结点
sb.append(preOrder(root.left)); // 前序遍历左子树
sb.append(preOrder(root.right)); // 前序遍历右子树
return sb.toString();
}
} 7、如何写好递归式
对于上面例题,如求阶乘n!,如果n = 100,很显然这段程序需要递归地调用自身100次。这样调用深度至少就到了100。栈的大小是有限的,当n变的更大时,有朝一日总会使得栈溢出,从而程序崩溃。除此之外,每次函数调用的开销会导致程序变慢。所以说这段程序十分不好。那什么是好的递归,如何递归能够将问题的规模缩小,那就是好的递归。
怎样才算是规模缩小了呢。举个例子,比如要在一个有序数组中查找一个数,最简单直观的算法就是从头到尾遍历一遍数组,这样一定可以找到那个数。如果数组的大小是N,那么我们最坏情况下需要比较N次,所以这个算法的复杂度记为O(N)。有一个大名鼎鼎的算法叫二分法,它的表达也很简单,由于数组是有序的,那么找的时候就从数组的中间开始找,如果要找的数比中间的数大,那么接着查找数组的后半部分(如果是升序的话),以此类推,知道最后找到我们要找的数。稍微思考一下可以发现,如果数组的大小是N,那么最坏情况下我们需要比较logN次(计算机世界中log的底几乎总是2),所以这个算法的复杂度为O(logN)。
简单的分析一下二分法为什么会快。可以发现二分法在每次比较之后都帮我们排除了一半的错误答案,接下去的一次只需要搜索剩下的一半,这就是说问题的规模缩小了一半。而在直观的算法中,每次比较后最多排除了一个错误的答案,问题的规模几乎没有缩小(仅仅减少了1)。这样的递归就稍微像样点了。
重新看阶乘的递归,每次递归后问题并没有本质上的减小(仅仅减小1),这和简单的循环没有区别,但循环没有函数调用的开销,也不会导致栈溢出。所以结论是如果仅仅用递归来达到循环的效果,那还是改用循环吧。
总结一下,递归的意义就在于将问题的规模缩小,并且缩小后问题并没有发生变化(二分法中,缩小后依然是从数组中寻找某一个数),这样就可以继续调用自身来完成接下来的任务。我们不用写很长的程序,就能得到一个十分优雅快速的实现。
1. 先一般,后特殊(边界)。先写递归的主体部分,再回头写边界(一行行读主体部分的代码,寻找特殊的边界情况)
2. 每次调用必须缩小问题规模。
3. 每次问题规模缩小程度必须为1(不要贪心)这里的1并不是狭义的,比方说如果二分查找的时候,每次缩小一半的规模也是可以的 。
8、练习:
1、猴子摘了一堆桃子,第一天吃了一半,觉得不过隐又吃了一个;第二天吃了剩下的一半零一个;以后每天如些,到第十天,猴子一看只剩下一个了。问最初有多少个桃子。
2、“Fibonacci兔子问题”:从某年某月(设为第0月)开始,把雌雄各一的一对小兔放入养殖场,假定两个月后长成成兔,并同时(即第二个月)开始每月产雌雄各一的一对小兔,新增的小兔也按此规律繁殖,问第n个月末养殖场共有多少对兔子?
3、用递归方法求两个数m和n的最大公约数。