【数据结构】初入数据结构的二叉树( Binary Tree)以及Java代码实现

初入数据结构的二叉树( Binary Tree)以及Java代码实现

---

• 前提概念
  • 什么是树？
  • 什么是二叉树？
• 二叉树
  • 二叉树的特性
• 二叉树的类别
  • 满二叉树
  • 完全二叉树
  • 斜树
• 二叉树的存储结构
  • 顺序存储
  • 链式存储
• 二叉树的遍历
  • 深度优先遍历和广度优先遍历
  • 前序遍历
  • 中序遍历
  • 后序遍历
  • 层次遍历

前提概念

---

什么是树？

我们知道数据结构中的树，是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树, 那它的具体定义是什么呢？

百度百科的定义：

树（tree）是包含n（n>=0）个结点的有穷集，其中：

• 每个元素称为结点（node）；
• 有一个特定的结点被称为根结点或树根（root）。
• 除根结点之外的其余数据元素被分为m（m≥0）个互不相交的集合T1，T2，……Tm-1，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）

简单的说就是，一颗树由根结点和m(m>=0)棵子树构成，或者说由n(n>=0)个结点构成一颗树；如果某棵树没有结点，即n = 0 ，那这就是一颗空树；即使只有一个结点，没有子树，依然可以构成一颗树,即n = 1,m = 0

什么是二叉树？

二叉树的定义

• 首先要是一颗树，满足树的基本定义
• 本身是有序树；
• 树中各个节点的度不能超过 2。即只能是 0、1 或者 2

满足上面三个条件的存储结构就是一个颗二叉树

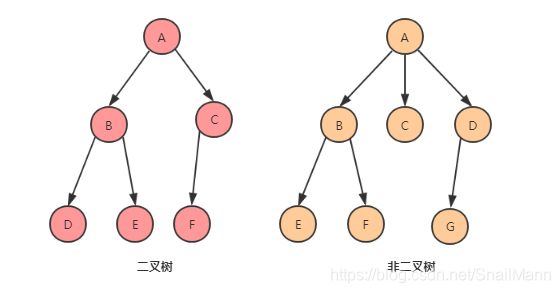
看上图，我们知道，这个图上有两棵树，的确也满足树的定义，既满足二叉树的第一个条件：是颗树; 然后这两颗树，是不是有序的，我就不知道了，就当做是有序的吧，所以两棵树都满足二叉树的第二个条件：有序树; 然后第三个条件是树的每个结点度不超过2，只能是0,1,2。行，观察之后，我们就可以很简单的知道了，左边的树满足条件，右边的树不满足条件，因为右边的树的根结点A的度是3，超过了二叉树的度不超过2的限制

二叉树

---

二叉树的特性

二叉树可以由三个重点关注的特性：

• 二叉树中，第i层最多有2^(i-1)个结点
• 深度为n的二叉树，整棵树最多有(2^n)-1个结点，为什么减1，因为根结点只有一个呀，没有成双成对
• 二叉树中，叶子结点树为n1, 度为2的结点树为n2，那么n1 = n2 + 1;

性质 3 的计算方法为：

• 对于一个二叉树来说，除了度为 0 的叶子结点和度为 2 的结点，剩下的就是度为 1 的结点（设为 n1），那么总结点 n=n0+n1+n2。
• 同时，对于每一个结点来说都是由其父结点分支表示的，假设树中分枝数为 B，那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的，即 B=n1+2n2。所以，n 用另外一种方式表示为 n=n1+2n2+1。 两种方式得到的 n 值组成一个方程组，就可以得出n0=n2+1。

要记住，只知道结点数，是不能知道普通二叉树的高是多少的，log2n的是满二叉树

二叉树的类别

---

我们知道了二叉树的定义，以为二叉树就这样啦？其实二叉树还可以继续分类，比如衍生出了满二叉树和完全二叉树的定义

满二叉树

满二叉树的定义

• 在二叉树定义的基础上，还满足除了叶子结点以外的所有结点的度都是2话，那么该二叉树就是一颗满二叉树

简而言之，就是分支结点以及根结点的度全都是2，如下图

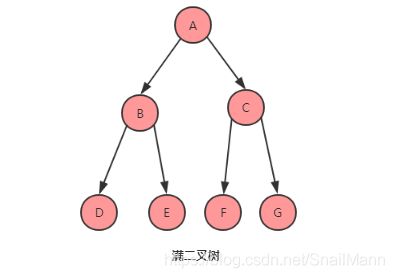
满二叉树有什么特性要记住的吗？ 必须的，除了满足普通二叉树的特性外，还满足

• 满二叉树的第i层的结点数必为2^(n-1)
• 深度为n的满二叉树整棵树必有(2^n) - 1个结点，叶子结点必为2^(n-1)个
• 满二叉树中不存在度为1的结点，每一个分支结点都有两棵深度一样的子树，且叶子结点都在同一层，最底层
• 具有n个结点的满二叉树的高是log2(n + 1)，2为底的对数函数，为什么n + 1，因为满二叉树的结点数必为奇数（因为根结点不是成双成对的），所以 + 1变成偶数，才能知道树高是多少

完全二叉树

完全二叉树的定义：

• 在二叉树的基础上，除去最底层结点后，是一棵满二叉树，且没去前的最后一层的结点是依次从左到右分布的，则此二叉树则是一棵完全二叉树
• 满二叉树也是一棵完全二叉树，但完全二叉树就不一定是一棵满二叉树了

红树是一棵满二叉树，必然是一棵完全二叉树；紫树去掉最后一层是一棵满二叉树，没去前的最后一层的结点满足从左到右的分布，是一棵完全二叉树；蓝树去掉最后一层是一棵满二叉树，但是没去前的最后一层结点不符合从左到右的分布，所以不是一棵满二叉树；绿树去掉最后一层就不是一棵满二叉树，所以必然不是一棵完全二叉树

有什么要记住的完全二叉树特性呢？

• 满二叉树必然是一棵完全二叉树，但完全二叉树就不一定是一棵满二叉树

对于任意完全二叉树，对完全二叉树从左向右，从上往下标号的话(如上图)，对于结点i，完全二叉树有几个结论可以成立：

• 当 i>1 时，父亲结点为结点[i/2]。（i=1 时，表示的是根结点，无父亲结点）
• 如果 2*i>n（总结点的个数） ，则结点i肯定没有左孩子（为叶子结点）；否则其左孩子是结点2*i
• 如果 2*i+1>n ，则结点 i肯定没有右孩子；否则右孩子是结点 2*i+1

斜树

斜树定义：

• 所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树

二叉树的存储结构

---

二叉树的存储结构有两种，分别为顺序存储和链式存储。

顺序存储

二叉树的顺序存储，指的是使用顺序表（数组）存储二叉树。需要注意的是，经验总结指出只有完全二叉树才可以使用顺序表存储。(满二叉树也可以使用顺序存储, 因为满二叉树本身就是完全二叉树)

因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树。

完全(满)二叉树的顺序存储

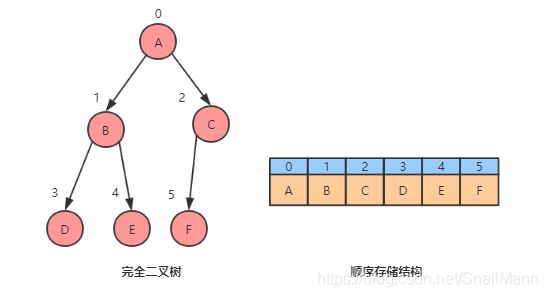
看上图啦，我们知道二叉树是一棵有序树，所以完全二叉树也肯定是一棵有序树。因为有序，所以我们可以给树的结点从上到下，从左到右开始顺序标号。为什么要标号呢? 看右边的顺序存储结构就知道了，我们要把结点数据扔到对应的数组索引位置，对号入座。所以将完全二叉树的数据使用顺序存储的话，那么对应的数据结构就是上图的右边；不多不少，6个结点的完全二叉树刚好使用长度为6的数组就可以完美覆盖

那么为什么普通二叉树，既非完全(满)二叉树不适合用顺序结构存储呢？因为会浪费大量空间！！ 看下图

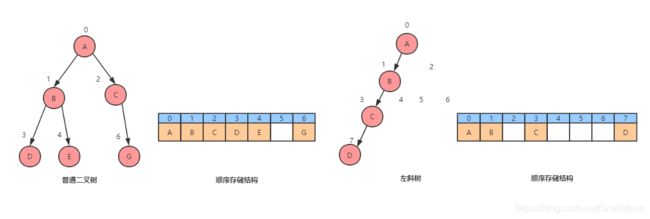
如果对普通二叉树(斜树也是二叉树的一种)进行顺序标号，作为数组的索引，那么把二叉树的数据放入数组中，就会发现很多地方都是空着的，使用不到的，这就会造成很大的数据数据浪费啦; 所以才说只有完全(满)二叉树才适合顺序存储

链式存储

比较完全(满)二叉树仅仅是二叉树分类中的一种，那么广大的普通二叉树用什么形式存储呢？那我们就可以使用链式存储啦。

二叉树结点数据结构
因为二叉树是有序数，又每个结点至多有棵子树，又称左子树和右子树，所以链式存储结合二叉树的这个特点，通常会将二叉树的结点数据结构TreeNode定义为一个数据域data和两个指针域lchild,rchild

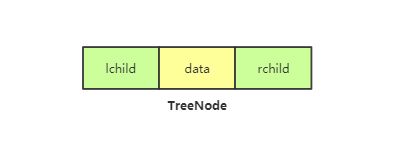
将树转出成链式存储大致就如下图所示

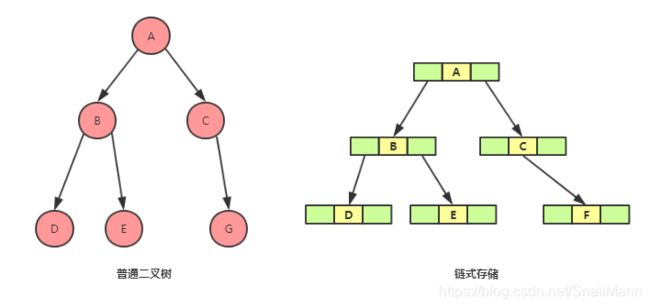
public class TreeNode<E> {
        //数据域
        private E data;
        //左子树，右子树指针域
        private TreeNode<E> lchild, rchild;
}

二叉树的遍历

---

二叉树的遍历时二叉树知识点的重点考察对象，二叉树遍历指的是从树的根结点出发，按照某种次序规则访问二叉树中的所有结点，使得每个结点有且仅被访问一次

深度优先遍历，广度优先遍历

二叉树有两种遍历方式，深度优先遍历和广度优先遍历

• 深度优先遍历（Depth First Search, DFS）
  • 前序遍历
  • 中序遍历
  • 后序遍历
• 广度优先遍历（Breadth First Search, BFS）
  • 层次遍历

前序遍历

什么是前序遍历?

• 先访问根结点
• 再访问左子树的根结点
• 再访问右子树的根结点

前序比较简单，也比较好理解，所以就多说啦

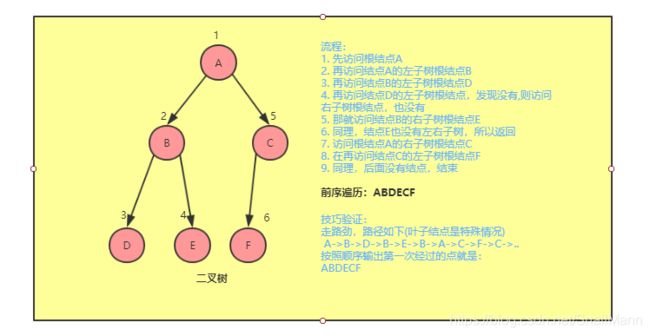
中序遍历

什么是中序遍历?

• 先访问左子树的根结点
• 再访问当前根结点
• 再访问右子树的根结点

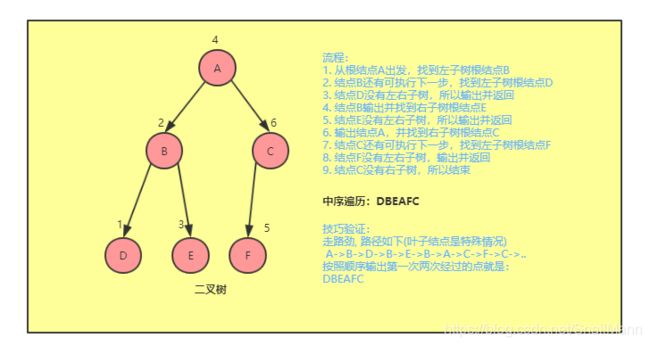
要理解每一步的遍历，既每一次的访问结点，在决定是否输出该结点前，要看该结点是否有可执行的下一步，如果没有，则输出，如果有则需要判断某序遍历的输出顺序

后序遍历

什么是后序遍历?

• 先访问左子树的根结点
• 再访问右子树的根结点
• 再访问当前根结点

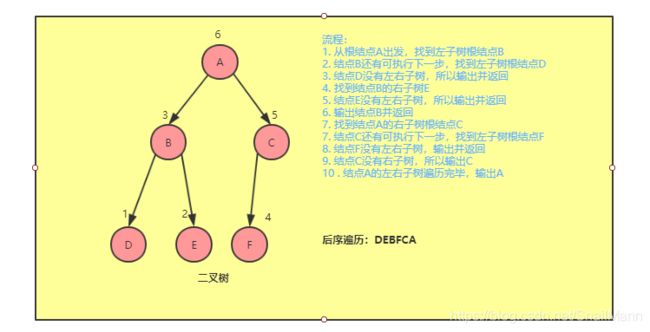
其实后序遍历也是一种特殊的前序的逆序，什么是特殊的前序？

• 正常前序是根->左->右，这里的特殊指的是这个前序的规则是根->右->左
• 什么是逆序，就是后序实质上是特殊前序根->右->左的输出结果的倒序，既得到根->右->左结果后，倒过来输出就是一个后序了

你可以试试~写代码的时候，也可以这么尝试

层次遍历

什么是层次遍历?

• 层次遍历就更好理解的，就是自上而下，从左到右的依次遍历，每一层每一层的遍历，当上一层遍历完了，才到下一层开始遍历

知道前，中序，求后序

例如知前中，求后序

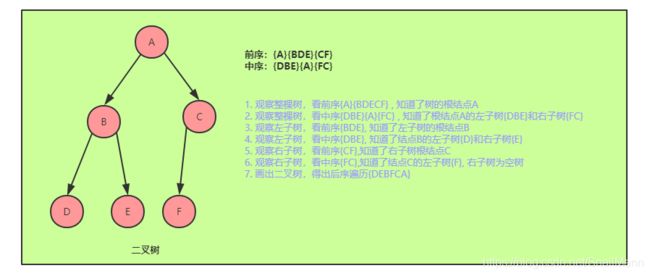
• 前序遍历：ABDECF 中序遍历：DBEAFC

知道前序和中序，求后序的方法就是，根据前序和中序的特点，先画出正棵树，再根据树来写后序遍历

前序遍历有什么特点呢？前序遍历的第一个结点肯定是树的根结点，中序遍历有什么特点呢？根据前序知道的根结点，我们可以在中序遍历中知道根结点的左子树和右子树

• 根据前序遍历的特点，我们知道结点A肯定是根结点，所以我们在从中序遍历可知，A左边有三个结点{DBE}, 右边有两个结点{FC}, 所以我们现在知道了根结点A和其左右子树
• 观察左子树{DBE}, 看前序遍历中左子树的顺序是{BDE}, 所以B是左子树的根结点，在看中序遍历可知，D是结点B的左孩子，E是结点B的右孩子，解决正棵树的左子树
• 观察右子树{FC} , 看前序遍历中右子树的顺序是{CF}, 所以右子树的根结点是C， 在根据中序遍历的结果可知，F在C的左边，所以F是结点C的左孩子，结点C没有右孩子 ，解决正棵树的右子树

知道后，中序，求前序

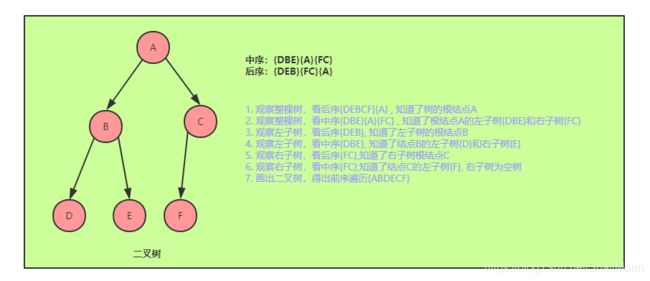
例如知前中，求后序

• 后序遍历：DEBFCA 中序遍历：DBEAFC

其实道理都是同上的，就不说的太详细了, 后序的最后一结点肯定是树的根结点，中序同上

二叉树Java实现

---

• 二叉树的高（递归）
• 二叉树的先序遍历（迭代，递归）
• 二叉树的中序遍历（迭代，递归）
• 二叉树的后序遍历（迭代，递归）
• 二叉树的层次遍历（迭代）
• 根据前序和中序序列重建二叉树（递归）

/**
 * 链式存储实现的二叉树
 */
public class BinaryTree<T> {

    public static class TreeNode<E> {

        /**
         * 数据域
         */
        private E data;

        /**
         * 左子树，右子树指针域
         */
        private TreeNode<E> lchild, rchild;

        public TreeNode(E data) {
            this.data = data;
        }


        public E getData() {
            return data;
        }

        public void setData(E data) {
            this.data = data;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;

            TreeNode<?> treeNode = (TreeNode<?>) o;

            if (data != null ? !data.equals(treeNode.data) : treeNode.data != null) return false;
            if (lchild != null ? !lchild.equals(treeNode.lchild) : treeNode.lchild != null) return false;
            return rchild != null ? rchild.equals(treeNode.rchild) : treeNode.rchild == null;
        }

        @Override
        public int hashCode() {
            int result = data != null ? data.hashCode() : 0;
            result = 31 * result + (lchild != null ? lchild.hashCode() : 0);
            result = 31 * result + (rchild != null ? rchild.hashCode() : 0);
            return result;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "data=" + data +
                    ", lchild=" + lchild +
                    ", rchild=" + rchild +
                    '}';
        }
    }

   /*
	* 树结点的个数
	*/
    private int nodeCount;
    private TreeNode<T> rootNode;


    public BinaryTree(TreeNode<T> rootNode) {
        this.rootNode = rootNode;
        nodeCount = 1;
    }


    public BinaryTree() {
        this.rootNode = null;
        nodeCount = 0;
    }

    /**
     * 获得结点数
     *
     * @return
     */
    public int getNodeCount() {
        return nodeCount;
    }

    /**
     * 求树的高
     *
     * @return
     */
    public int height() {
        return depthForTree(rootNode);
    }

    /**
     * 求某棵子树的深度
     *
     * @param root
     * @return
     */
    private int depthForTree(TreeNode<T> root) {
        if (root == null) {
            return 0;
        }
        return Math.max(depthForTree(root.lchild), depthForTree(root.rchild)) + 1;
    }

    /**
     * 方法1
     * 由先序序列和中序序列构建二叉树
     */
    public TreeNode<T> createTreeByPreMidMethod1(T[] preArray, T[] midArray) {
        //递归出口，当有一者长度为空时，代表数组有误
        if (preArray.length == 0 || midArray.length == 0) {
            return null;
        }

        /**
         * 构建根结点
         * 如果根结点为空，则要设置根结点
         * 如果根结点已存在，则无需设置根结点
         */
        TreeNode<T> root = new TreeNode<>(preArray[0]);
        if (this.rootNode == null) {
            this.rootNode = root;
        }

        //遍历中序数组
        for (int i = 0; i < midArray.length; i++) {
            //在中序数组中找到根结点的索引位置，i虽然是索引，实际上代表(左子树的结点个数 - 1)
            if (root.data == midArray[i]) {
                /**
                 * 构建左子树
                 * 1. Arrays.copyOfRange是为了方便，[from,to)区间
                 * 2. 前序数组需要截取左子树的区间，作为新的子树前序数组
                 * 3. 中序数组需要截取左子树的区间，作为新的子树中序数组
                 */
                root.lchild = createTreeByPreMidMethod1(Arrays.copyOfRange(preArray, 1, 1 + i), Arrays.copyOfRange(midArray, 0, i));
                /**
                 * 构建右子树
                 * 1. Arrays.copyOfRange是为了方便，[from,to)区间
                 * 2. 前序数组需要截取右子树的区间，作为新的子树前序数组
                 * 3. 中序数组需要截取右子树的区间，作为新的子树中序数组
                 */
                root.rchild = createTreeByPreMidMethod1(Arrays.copyOfRange(preArray, i + 1, preArray.length), Arrays.copyOfRange(midArray, i + 1, midArray.length));
            }
        }

        //递归出口，正常构建，返回构建树的根结点
        return root;
    }

    /**
     * 根据前序和中序构建二叉树 | 标准
     * 1. 如果前序序列和中序序列为Null或长度为0，直接返回
     * 2. 如果前序序列和中序序列的长度不一致，则为错误序列，直接返回
     *
     * @param preArray
     * @param midArray
     * @return
     */
    public TreeNode<T> createTreeByPreMidMethod2(T[] preArray, T[] midArray) {
        if (preArray == null || preArray.length == 0
                || midArray == null || midArray.length == 0) {
            return null;
        }
        if (preArray.length != midArray.length) {
            return null;
        }

        return createTreeByPreMidMethod2(preArray, 0, preArray.length - 1, midArray, 0, midArray.length - 1);
    }

    /**
     * 构建子树二叉树，根据前序和中序序列
     * 1. 通过前序序列，得知根结点
     * 2. 通过中序序列，比较根结点，得到根节点在中序序列的位置，就可以知道，左子树结点的个数，以及右子树结点的个数
     * 3. 然后递归求左子树和右子树
     *
     * @param preArray
     * @param preStart
     * @param preEnd
     * @param midArray
     * @param midStart
     * @param midEnd
     * @return
     */
    private TreeNode<T> createTreeByPreMidMethod2(T[] preArray, int preStart, int preEnd, T[] midArray, int midStart, int midEnd) {

        //递归退出条件一
        if (midStart > midEnd || preStart > preEnd) {
            return null;
        }

        //获得该树的根结点
        TreeNode<T> root = new TreeNode<>(preArray[preStart]);
        if (rootNode == null) {
            rootNode = root;
        }

        for (int i = midStart; i <= midEnd; i++) {
            if (root.data == midArray[i]) {
                /**
                 * 求左子树
                 * 左子树前序序列是从[preStart + 1,preStart到i - midStart个长度]，为什么是i - midStart?
                 * 我们知道从前序看，preStart + 1就是左子树的根节点，而这个左子树的长度是多少呢？就要从中序看，根节点左边的所有都是左子树结点，有多少个呢？就是 （i - midStart）个
                 * （i刚好就是根结点，但因为i是索引，如果索引是从0开始算，那么左子树结点就刚好是i个，如果不是从0开始，而是从某个索引a开始，那么i - a才能得到左子树结点真实的个数）
                 *
                 */
                root.lchild = createTreeByPreMidMethod2(preArray, preStart + 1, preStart + (i - midStart), midArray, 0, i - 1);

                /**
                 * 求右子树
                 */
                root.rchild = createTreeByPreMidMethod2(preArray, preStart + i - midStart + 1, preEnd, midArray, i + 1, midEnd);
            }
        }

        return root;


    }

    /**
     * 为某个结点添加左孩子
     *
     * @param lchild
     * @param parent
     * @return
     */
    public TreeNode<T> addLChild(TreeNode<T> lchild, TreeNode<T> parent) {
        if (parent.lchild == null) {
            parent.lchild = lchild;
            nodeCount++;
            return lchild;
        }
        throw new RuntimeException("该结点已存在左子结点");

    }


    /**
     * 为某个结点添加右孩子
     *
     * @param rchild
     * @param parent
     * @return
     */
    public TreeNode<T> addRChild(TreeNode<T> rchild, TreeNode<T> parent) {
        if (parent.rchild == null) {
            parent.rchild = rchild;
            nodeCount++;
            return rchild;
        }
        throw new RuntimeException("该结点已存在右子结点");

    }


    /**
     * 查找某个结点的孩子结点
     *
     * @param node
     * @return
     */
    public List<TreeNode<T>> listChildNode(TreeNode<T> node) {
        List<TreeNode<T>> childrens = new LinkedList<>();
        if (node.lchild != null) {
            childrens.add(node.lchild);
        }
        if (node.rchild != null) {
            childrens.add(node.rchild);
        }
        return childrens;

    }

    /**
     * 查找某个结点的父结点
     *
     * @param node
     * @return
     */
    public TreeNode<T> getParentNode(TreeNode<T> node) {
        if (node == null) {
            throw new RuntimeException("error");
        }
        return getParentNode(rootNode, node);
    }

    /**
     * 查找子树中，某个结点的父结点
     *
     * @param root
     * @param node
     * @return
     */
    private TreeNode<T> getParentNode(TreeNode<T> root, TreeNode<T> node) {
        //当前结点为null， 直接返回，函数出口
        if (root == null) {
            return null;
        }

        //当前结点的左孩子或右孩子是目标节点，则代表当前结点是目标结点的父结点，函数出口
        if (root.lchild == node || root.rchild == node) {
            return root;
        }

        //否则递归，先递归左子树
        TreeNode<T> result = getParentNode(root.lchild, node);
        //如果左递归没有发现符合条件，既result == null时，才开始右递归，如果已经发现了就不右递归了，直接返回结果
        if (result == null) {
            result = getParentNode(root.rchild, node);
        }


        return result;


    }


    /**
     * 先序遍历 | 递归
     */
    public void preOrder() {
        preOrder(rootNode);
        System.out.println();
    }

    /**
     * 先序遍历以node为根结点的树
     *
     * @param node
     */
    private void preOrder(TreeNode<T> node) {
        // 若二叉树不为空
        if (node != null) {
            System.out.print(node.data);// 访问当前结点
            preOrder(node.lchild);// 按先跟次序遍历当前结点的左子树
            preOrder(node.rchild);// 按先跟次序遍历当前结点的右子树
        }
    }

    /**
     * 中序遍历 | 递归
     */
    public void midOrder() {
        midOrder(rootNode);
        System.out.println();
    }

    /**
     * 对node为根节点的子树进行中序遍历
     *
     * @param node
     */
    private void midOrder(TreeNode<T> node) {
        if (node != null) {
            midOrder(node.lchild);
            System.out.print(node.data);
            midOrder(node.rchild);
        }
    }

    /**
     * 后序遍历 | 递归
     */
    public void postOrder() {
        postOrder(rootNode);
        System.out.println();
    }

    /**
     * 对以node为根结点的子树进行后序遍历
     *
     * @param node
     */
    private void postOrder(TreeNode<T> node) {
        if (node != null) {
            postOrder(node.lchild);
            postOrder(node.rchild);
            System.out.print(node.data);
        }
    }


    /**
     * 先序遍历 | 循环 | 栈实现 |  先进后出
     * 

     * 1. 每次循环相当于访问一棵子树
     * 2. 每次访问子树都要根据某序遍历的规则进行访问
     * 3. 栈用来存储之前访问过的结点的，用于回溯
     * 4. 首先条件就是要相对根结点不为空，已经用于回溯的栈不为空，如果都为空，肯定代表遍历已结束
     * 5. 从根结点找，遍历子树，一直找下去，遍历一个结点输出一个，同时用栈记录下来，用于回溯
     * 6. 当找到一个结点为空，则回溯结点，找其右子树
     */
    public void preOrderIteration() {
        Deque<TreeNode<T>> stack = new ArrayDeque<>();
        TreeNode<T> root = this.rootNode;

        //结点不为空，或者栈不为空，如果两者都是空，则遍历完毕
        while (root != null || !stack.isEmpty()) {
            //如果相对根结点不为空，有下一步，不需要回溯
            if (root != null) {
                //则先序输出根结点
                System.out.print(root.data);
                //将结点入栈
                stack.push(root);
                //遍历当前结点的左子结点
                root = root.lchild;
            } else {
                //如果相对根结点为空 | 或者当前结点为空，没有可行下一步了，需要回溯
                //出栈获得上一个结点
                root = stack.pop();
                //则找上一个结点右子树
                root = root.rchild;
            }
        }
        System.out.println();
    }

    /**
     * 中序遍历 | 循环 | 栈实现 |  先进后出
     * 

     * 1. 中序就是回溯时再输出
     */
    public void midOrderIteration() {
        Deque<TreeNode<T>> stack = new ArrayDeque<>();
        TreeNode<T> root = this.rootNode;

        while (root != null || !stack.isEmpty()) {
            if (root != null) {
                stack.push(root);
                root = root.lchild;
            } else {
                root = stack.pop();
                System.out.print(root.data);
                root = root.rchild;
            }
        }
        System.out.println();


    }

    /**
     * 后序遍历 | 循环 | 栈实现 | 先进后出
     * 

     * 1. 这个后序的实现非常巧妙特别，后序实际是逆前序的实现，我们知道前序是根->左->右；后序是左->后->根。但后序其实还可以这么思考，既根->右->左，得到的就是后序的逆序，这根右左就非常像前序遍历了
     * 2. 模拟前序遍历一样的逻辑，只不过与前序不同的是，先右再左，所以当node != null时，把访问结点存储到stack中，用于回溯，同时记录到output中，用于倒序输出
     * 3. 其他跟前序是一样的，只不过后序是根右左的倒序罢了，所以需要一个栈用来存储，并倒序输出
     */
    private void postOrderIteration() {
        if (rootNode == null) {
            return;
        }
        Deque<TreeNode<T>> stack = new ArrayDeque<>();
        Deque<TreeNode<T>> output = new ArrayDeque<>();
        TreeNode<T> node = rootNode;
        while (node != null || !stack.isEmpty()) {
            if (node != null) {
                stack.push(node);
                output.push(node);
                node = node.rchild;
            } else {
                node = stack.pop();
                node = node.lchild;
            }
        }
        while (!output.isEmpty()) {
            System.out.print(output.pop().data);
        }
        System.out.println();
    }


    /**
     * 层次遍历 | 循环 | 队列实现 | 先进先出
     * 1. 层次遍历就是从第一层开始到最底层，从每层的左边到右边遍历
     * 2. 利用队列的先进先出特性，树的所有结点都会进入队列，除了根结点
     * 3. 首先结点不为空，我们就继续遍历，因为node的除了是根结点，就是队列中存储的树的其他结点，不可能为空，当空时，就代表队列已经出队完毕
     * 4. 每次循环就是遍历某个结点左右孩子的过程，遍历结束后，需要出队一个结点，作为下次遍历的结点
     */
    public void levelOrder() {
        Deque<TreeNode<T>> queue = new LinkedList<>();
        TreeNode<T> root = this.rootNode;
        while (root != null) {
            System.out.print(root.data);
            if (root.lchild != null) {
                // 相对根结点的左孩子结点入队
                queue.offer(root.lchild);
            }
            if (root.rchild != null) {
                // 相对根结点的右孩子结点入队
                queue.offer(root.rchild);
            }
            //队列队头出队，相对根结点指向出队结点 ,若队列空返回null
            root = queue.poll();
        }
        System.out.println();
    }

    public static void main(String[] args) throws Exception {
        TreeNode<Integer> node1 = new TreeNode<>(1);
        TreeNode<Integer> node2 = new TreeNode<>(2);
        TreeNode<Integer> node3 = new TreeNode<>(3);
        TreeNode<Integer> node4 = new TreeNode<>(4);
        TreeNode<Integer> node5 = new TreeNode<>(5);
        TreeNode<Integer> node6 = new TreeNode<>(6);
        TreeNode<Integer> node7 = new TreeNode<>(7);
        BinaryTree<Integer> binaryTree = new BinaryTree<>();
        /* binaryTree.createTreeByPreMid(new Integer[]{1, 2, 4, 5, 3, 6, 7}, new Integer[]{4, 2, 5, 1, 6, 3, 7});*/
        binaryTree.createTreeByPreMidMethod2(new Integer[]{1, 2, 4, 5, 3, 6, 7}, new Integer[]{4, 2, 5, 1, 6, 3, 7});

      /*  binaryTree.addLChild(node2, node1);
        binaryTree.addRChild(node3, node1);
        binaryTree.addLChild(node4, node2);
        binaryTree.addRChild(node5, node2);
        binaryTree.addLChild(node6, node3);
        binaryTree.addRChild(node7, node3);*/
        System.out.println("递归");
        binaryTree.preOrder();
        binaryTree.midOrder();
        binaryTree.postOrder();
        System.out.println("循环|栈实现");
        binaryTree.preOrderIteration();
        binaryTree.midOrderIteration();
        binaryTree.postOrderIteration();
        binaryTree.levelOrder();

    }


}

参考资料

---

• 深入学习二叉树(一) 二叉树基础 - @作者：MrHorse1992
• 什么是二叉树，二叉树及其性质详解 - @作者：解学武
• 二叉树前序、中序、后序遍历相互求法 - @作者：尤教授
• Java实现二叉树先序，中序，后序遍历 - @作者：Animationer
• 根据前序遍历和中序遍历的结果，重建二叉树- @作者：Reallycold