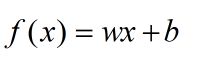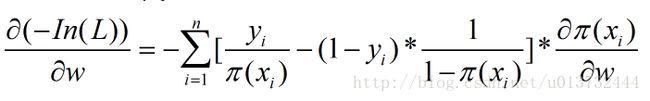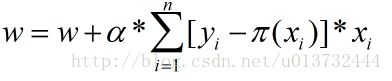Logistics回归

1.什么是Logistics？

Logistics回归虽然后缀回归，但是不属于回归算法，而是分类算法。该算法通过在样本空间中寻找一个分类超平面，将正负样本分别分到互不相交的两个子空间中。

2、算法公式推导

    数据准备：logistics算法需要使用数值型数据，对于标称型数据需要转换为数值型数据，为了加速收敛，通常会对原始数据进行标准化。

它是对感知机算法的一种改良版，感知机算法的模型如下所示：

                                      

w为每一个特征的权重值，b为偏置。

    Logistics算法在此基础上通过一个sigmoid函数，将取值区间为负无穷到正无穷的距离映射到[0,1]区间，通过指定一个阈值（通常选取0.5），将结果大于或等于0.5的判定为正类，将结果小于0.5的判定为负类。算法模型如下公式：

                                    

    则有p(1|x)=f(x),p(0|x)=1-p(1|x),这个判定值并不是概率，而只是表示为正类的趋势、可能，因为wx越大，f(x)越趋近于1。sigmoid函数映射后的值并不是均匀的，也就是说x1/x2！=f(x1)/f(x2)，通过作图可以看出，这个曲线在0附近变化显著，越趋近两端越平缓。如下图所示，横坐标的数值对应于wx：

                                  

Logistics算法将这个值作为概率，通过求似然函数,对似然函数取负对数作为要优化的损失函数。

令π(x)=p(1|x),对于xi怎有如下函数：

                                                     

将i=1,2,3...,n累乘。

                                   

取负对数：

                                   

    上式即为要优化的损失函数，有个很霸气的名字--交叉熵

    交叉熵的模型如下所示：

                                   

    将原式中的负号移入对数中，即为上面的形式，p(i)为真实的分布，q(i)为预测的分布，对应到原式就是yi或（1-yi)为真实的分布，是原数据给定的事实，而π(xi)为训练的模型，预测的分布。交叉熵作为损失函数的一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。这个很好理解，因为使用sigmoid函数，在0附近的变化是非常快的，在两端变化慢，这个和平方损失函数正好相反，平方损失函数越趋向两端变化越快，越趋向0附近变化越慢。而在分类问题中，往往靠近0附近的点更有助于决定分类超平面，Sigmoid函数将wx映射到[0,1]区间，所以在0附近的值变化相当对其它区间的变化是非常明显的，也就是对靠近分类超平面的点非常敏感。

当yi=1,如果π(xi)=1,则损失为0，如果π(xi)=1，则损失无穷大。

当yi=0,如果π(xi)=1，则损失为无穷大，如果π(xi)=0，则损失函数为0.

    通常对上面的损失函数采用梯度下降算法进行求解，损失函数对w求导，过程如下：

                                   

后面的一项求导为：

                                   

代入可得：

                                  

    对于上述的求解，通常有两种做法，一种是批梯度下降算法（Batch Gradient Descent）和随机梯度下降算法(Stochastic Gradient Descent ）。这两种算法的区别是，批梯度下降算法扫描整个数据集计算一次对参数值的更新，随机梯度下降算法每扫描一条数据就计算对参数值的更新。对于大量数据，随机梯度算法表现的性能更好，时间更快，通常只需要扫描部分数据就会收敛,但是随机梯度算法也会出现震荡无法收敛的情况。还有一种介于这两者之间的方式，Mini Batch Gradient Descent ，每次扫描一小部分数据计算对参数值的更新，这是对上面两种方法的一种权衡，相对于批梯度下降算法加快了计算速度，相对于随机梯度下降算法，确保了收敛。

批梯度下降算法的参数更新如下所示：

                                             

    上面的α为学习率，控制梯度下降的步长。

    随机梯度下降算法的参数更新如下所示：

                                            

3、算法实现

    下面给出上述算法的Python实现，分别使用批梯度下降和随机梯度下降：

#_*_encoding:utf-8_*_
import numpy as np

class LogisticsRegression:
    def __init__(self,alpha=0.01,type='SGD',iter_num=500):
        self.alpha=alpha
        self.iter_num=iter_num
        self.type=type

    def sigmoid(self, wx):
        return 1.0 / (1 + np.exp(-wx))

    def classify(self, wx):
        prob = self.sigmoid(wx)
        if prob > 0.5:
            return 1
        else:
            return 0

    def fit(self,trainX,trainY):
        self.trainX=trainX
        self.trainY=trainY
        if self.type=='SGD':
            self.SGD()
        else:
            self.BGD()

    def BGD(self):
        trainMat=np.mat(self.trainX)
        trainY=np.mat(self.trainY).T
        m,n=np.shape(self.trainX)
        self.w=np.ones((n,1))
        x=[]; y=[]
        for i in range(self.iter_num):
            error=trainY-self.sigmoid(trainMat*self.w)
            self.w=self.w+self.alpha*trainMat.T*error
            x.append((i+1)*m)
            y.append(self.calRatio())
        self.plotLearningCurve(x,y)

    def SGD(self):
        trainMat=np.mat(self.trainX)
        m,n=np.shape(self.trainX)
        self.w=np.ones((n,1))
        # x=[];y=[]
        for k in np.arange(self.iter_num):
            items=np.arange(m)
            np.random.shuffle(items)
            i=0
            for i in items:
                error=trainY[i]-self.sigmoid(trainMat[i]*self.w)
                self.w=self.w+self.alpha*trainMat[i].T*error[0]
        #         x.append((k+1)*m+i)
        #         y.append(self.calRatio())
        # self.plotLearningCurve(x,y)

    def calRatio(self):
        result=self.predict(self.trainX)
        m=np.shape(self.trainY)[0]
        count=0
        for i in range(m):
            if trainY[i]==result[i]:
                count=count+1
        return 1.0*count/m

    def plotLearningCurve(self,x,y):
        import matplotlib.pyplot as plt
        plt.plot(x,y)
        plt.show()

    def  predict(self,testX):
        m,n=np.shape(testX)
        testMat=np.mat(testX)
        result=[]
        for i in np.arange(m):
            result.append(self.classify(testMat[i]*self.w))
        return result

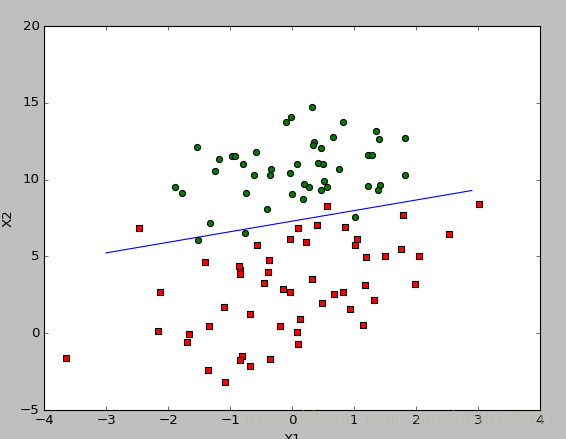
    def plotBestFit(self):
        import matplotlib.pyplot as plt
        dataArr = np.array(self.trainX)
        n = np.shape(dataArr)[0]
        xcord1 = []
        ycord1 = []
        xcord2 = []
        ycord2 = []
        for i in range(n):
            if int(self.trainY[i]) == 1:
                xcord1.append(dataArr[i, 1]);
                ycord1.append(dataArr[i, 2])
            else:
                xcord2.append(dataArr[i, 1]);
                ycord2.append(dataArr[i, 2])
        fig = plt.figure()
        ax = fig.add_subplot(111)
        ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
        ax.scatter(xcord2, ycord2, s=30, c='green')
        x = np.arange(-3.0, 3.0, 0.1)
        y = (-self.w[0] - self.w[1] * x) / self.w[2]
        ax.plot(x, y.T)
        plt.xlabel('X1');
        plt.ylabel('X2')
        plt.show()

def loadData(fileName):
    file=open(fileName)
    trainX=[]
    trainY=[]
    for line in file.readlines():
        items=line.strip().split('\t')
        x=[]
        x.append(1)
        for i in items[:-1]:
            x.append(np.float(i))
        trainX.append(x)
        trainY.append(np.int(items[-1]))
    return trainX,trainY


trainX,trainY=loadData('testSet.txt')
lr=LogisticsRegression(type='SGD')
lr.fit(trainX,trainY)
result=lr.predict(trainX)
lr.plotBestFit( )

数据下载链接：http://download.csdn.net/detail/u013732444/9830058

上面的绘制SGD的学习曲线图已经被注释，如果取消注释会非常耗时。

    使用批梯度训练结果如下：

    使用随机梯度下降结果如下所示：

4、梯度下降和随机梯度下降的比较

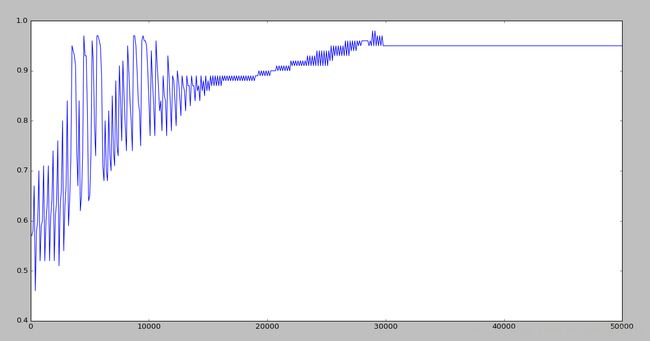
     这是BGD的训练效果和扫描次数的关系图：

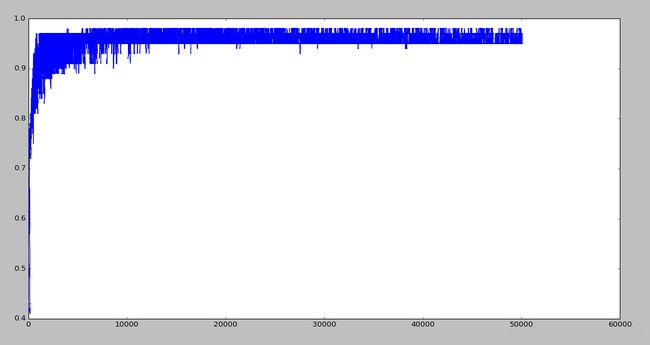
    下面是SGD的正确率和扫描样本个数的关系图：

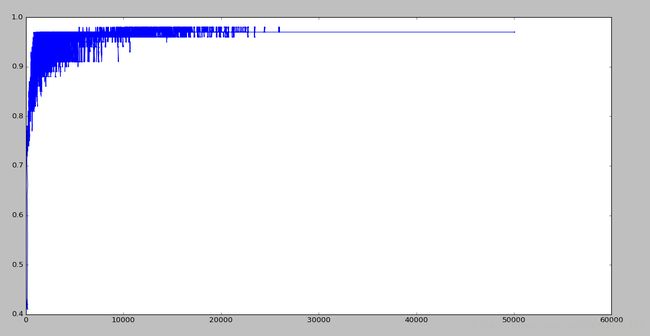
    很明显，随机梯度只需要扫描1000次样本就已经收敛，而批梯度下降算法需要扫描3000次才会收敛，节省了2/3的时间。但是仔细看，会发现，随机梯度下降一直在震动，并不是一个稳定的，而批梯度下降后期呈现一条直线达到收敛。这可以通过调节学习率进行改进，因为扫描一定次数后模型就已经收敛，因此可以调整学习率随扫描次数改变，使学习率逐渐减小趋近于0，因为后期已经没有必要学习了，可以使学习率与扫描样本的次数成反比，典型的有模拟退火算法。 这里通过简单的使学习率没扫描一遍训练样本就除以1.01的方式，减小学习率，效果如下所示：

但是，一定要注意这个学习率的变化设置，如果提前到收敛前就已经降低到趋近于0，那么容易欠拟合，也就是说模型还没有收敛，但是学习率已经很小，导致模型不学习了。

5、总结

    Logistics回归是一个二分类的学习算法，如果需要进行多分类，需要组合训练多个模型。该模型训练简单，需要存储的参数少，进行预测运算速度也快，工业上运用的较多，但是对异常点敏感。通常来说，LR是一个线性分类器，但是也可以使用核函数，处理非线性问题，对特征进行适当的组合也可以处理非线性问题，例如区分圆，X1^2+X2^2=k,如果使用X1,X2作为特征，那么是一个非线性可分问题，但是如果使用X1^2和X2^2那又是一个线性可分的问题，所以线性可分不可分没有必要用于衡量一个模型的能力。从损失函数可以看出，该算法模型的参与依赖于整个训练样本集，但是距离超平面近的点影响大，远的点影响小。这和支持向量机算法不同，支持向量机只依赖少量的样本点，移除其它样本不改变模型。

    位于判定边界附近的样本可以通过对阈值的改变而改变其分类，从而改变模型的正确率和召回率，这很容易满足工业对这些数据的需求。

    看其他人的博客总结经常会看到评价LR回归容易欠拟合，但是并没有看到什么解释。我个人觉得这应该可能是和它的损失函数有关，相较于SVM算法，LR损失函数的损失来源于整个训练样本集，sigmoid函数的取值区间为（0,1），也就是说无论一个点距离超平面多远，这个点多多少少都会贡献损失。而事实是已经存在大量的点，它距离分离超平面已经足够远，但是也提供了损失。当出现样本不均衡时，这个分类超平面就会以期望的分类超平面为基准向样本点少的一侧偏移，而实际应用中，样本正负比例1:100都很正常，所以这种欠拟合状态经常出现。而SVM，巧妙的剔除了那些明显正确的点，只关心少量样本点，在这个少量样本点中容易避免正负样本比例悬殊导致分类超平面出现偏移的问题。