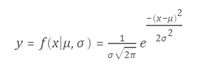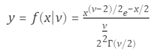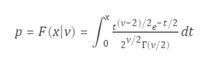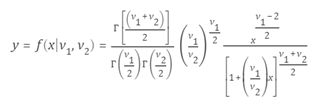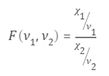数理统计四大分布---正态分布、卡方分布、学生t分布和F分布

在统计学上，我们会遇到一些常见的分布，除了正态分布外，，如t检验对应的t分布，检验对应的分布，方差分析对应的F分布等。这些分布是统计学的基础，在假设检验、方差分析等领域都起着至关重要的作用。在此，我们对这四种分布做详细的介绍，并附上MATLAB代码。

四种分布的讲解摘自MATLAB 2016的统计学和机器学习工具箱，有兴趣的可以去查看英文原版。

另外，为了方便，上传文档为图片格式，可能有些模糊，需要pdf或word原版的可以评论留下邮箱，有时间发送给大家。

 

一、正态分布

定义

正态分布的概率密度函数为

背景

正态分布是两个参数的曲线族，第一个参数µ是均值，第二个参数σ是标准差。标准正态分布(记为Φ(x)) 将 µ 设为0，将 σ 设为 1。

Φ(x) 在功能上与误差函数 erf有关

正态分布的第一次使用是对二项式的连续近似。使用正态分布进行建模的通常理由是中心极限定理，其中（大致）指出，当样本大小变为无穷大时，来自任何具有有限均值和方差的分布的独立样本的总和会收敛到正态分布。

参数

要可靠地使用平均值和标准差等统计参数，需要为它们提供一个好的估计器。 最大似然估计（MLE）提供一个这样的估计。 但是，MLE可能存在偏差，这意味着其参数的预期值可能与估计的参数不相等。 例如，MLE偏向于估计正态分布的方差。 通常用于估计正态分布参数的无偏估计是最小方差无偏估计（MVUE）。 MVUE具有参数的所有无偏估计的最小方差。

正态分布的参数μ和的MVUE是样本均值和方差。 样本均值也是μ的MLE。 以下是方差的两个常见公式。

                                                                                                                                                                                （1）

                                                                                                                                                                                （2）

其中

例如，假设您想要估计美国所有四年级儿童身高的平均值μ和方差。 函数normfit返回均值μ的MVUE和平方根的MVUE，以及μ和的置信区间。 这是一个有趣的例子，模拟随机选择的四年级班级学生的身高（英寸）。

rng default;                    % For reproducibility

height = normrnd(50,2,30,1);  % Simulate heights

[mu,s,muci,sci] = normfit(height)

mu =

   51.1038

s =

    2.6001

muci =

   50.1329

   52.0747

sci =

    2.0707

    3.4954

注意，s ^ 2是方差的MVUE。

s^2

ans =

    6.7605

例子

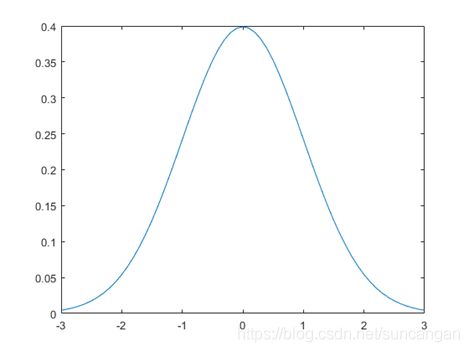
计算并绘制正态分布pdf

计算标准正态分布的pdf，参数 等于0且等于1。

x = [-3:.1:3];

norm = normpdf(x,0,1);

figure;

plot(x,norm)

二、卡方分布

综述

卡方分布通常用于假设检验，特别是拟合优度的卡方检验。

参数

参数	描述	备注
ν	自由度	ν 是非负整数

概率密度函数（pdf）

其中Γ（•）是Gamma函数，ν是自由度，x≥0。

累积分布函数（cdf）

其中Γ（•）是Gamma函数，ν是自由度，x≥0。

统计量描述

均值是 ν.

方差是2ν.

与其他分布的关系

 χ2分布是伽马分布的特殊情况，即下面的伽马分布的等式中b = 2。

χ2分布因其在正常采样理论中的重要性而受到特别关注。 如果一组n个观测值以方差分布，并且样本标准差是，那么

该关系用于计算normfit函数中的正态参数估计的置信区间。

例子

计算卡方分布的pdf

计算具有4个自由度的卡方分布的pdf。

x = 0:0.2:15;

y = chi2pdf(x,4);

figure;

plot(x,y)

卡方分布偏向右侧，特别是对于较小自由度。

 

三、学生氏t分布

综述

学生的t分布是一系列曲线，取决于单个参数ν（自由度）。

参数

学生的分布使用以下参数。

参数	描述
ν = 1, 2, 3,...	自由度

概率密度函数（pdf）

定义

学生t分布的概率密度函数（pdf）是

其中ν是自由度，Γ（•）是Gamma函数。 结果y是从具有ν自由度的学生t分布观察x的特定值的概率。

绘图

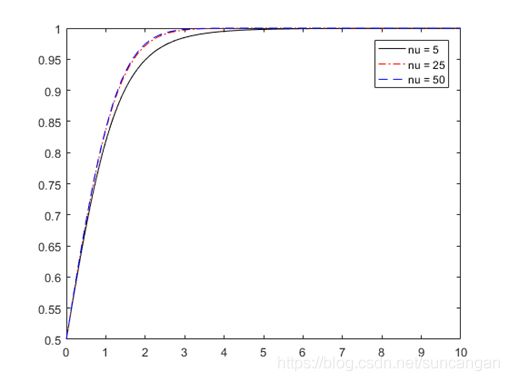
该图显示了如何改变自由度参数ν的值来改变pdf的形状。 对于三个不同的ν值，使用tpdf计算值x等于0到10的pdf。 然后在同一图上绘制所有三个pdf以进行视觉比较。

x = [0:.1:10];

y1 = tpdf(x,5);   % For nu = 5

y2 = tpdf(x,25);  % For nu = 25

y3 = tpdf(x,50);  % For nu = 50

figure;

plot(x,y1,'Color','black','LineStyle','-')

hold on

plot(x,y2,'Color','red','LineStyle','-.')

plot(x,y3,'Color','blue','LineStyle','--')

legend({'nu = 5','nu = 25','nu = 50'})

hold off

随机数生成

使用trnd从Student t分布中生成随机数。 例如，以下内容从Student t分布生成一个随机数，其自由度ν等于10。

nu = 10;

r = trnd(nu)

r =

    1.0585

和其他分布的关系

随着自由度ν变为无穷大，t分布接近标准正态分布。

如果x是来自具有平均μ的正态分布的大小为n的随机样本，则为统计量

是具有n-1自由度的学生t分布，其中是样本均值，s是样本标准差。

Cauchy分布是学生t分布，自由度ν为1.Cauchy分布具有不确定的均值和方差。

累积分布函数（cdf）

定义

学生t分布的cdf是

其中ν是自由度，Γ（•）是Gamma函数。 结果p是来自具有ν自由度的t分布的单个观测值将落在区间[-∞，x]中的概率。

绘图

该图显示了如何更改参数ν的值如何改变cdf的形状。 对于三个不同的ν值，使用tcdf计算值x等于0到10的cdf。 然后在同一图上绘制所有三个cdfs以进行视觉比较。

x = [0:.1:10];

y1 = tcdf(x,5);   % For nu = 5

y2 = tcdf(x,25);  % For nu = 25

y3 = tcdf(x,50);  % For nu = 50

figure;

plot(x,y1,'Color','black','LineStyle','-')

hold on

plot(x,y2,'Color','red','LineStyle','-.')

plot(x,y3,'Color','blue','LineStyle','--')

legend({'nu = 5','nu = 25','nu = 50'})

hold off

逆 cdf

使用tinv计算学生t分布的逆cdf。

p = .95;

nu = 50;

x = tinv(p,nu)

x =

    1.6759

均值和方差

学生氏t分布的均值为

mean=0

对于自由度ν大于1.如果ν等于1，则均值未定义。

学生t分布的方差是

自由度ν大于2.如果ν小于或等于2，则方差未定义。

使用tstat计算学生t分布的均值和方差。 例如，以下计算学生t分布的均值和方差，其自由度ν等于10。

nu = 10;

[m,v] = tstat(nu)

m =

     0

v =

    1.2500

例子

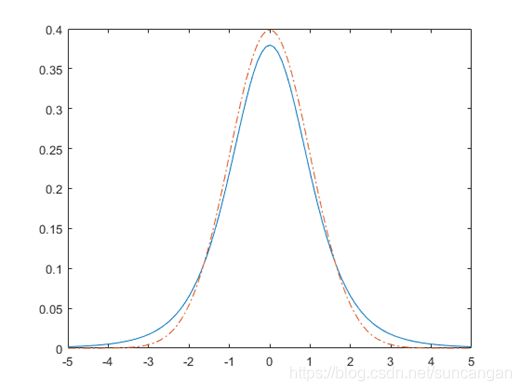
比较Student's t和标准正态分布的pdf 

计算参数nu = 5的Student t分布的pdf，以及标准正态分布。

x = -5:0.1:5;

y = tpdf(x,5);

z = normpdf(x,0,1);

在同一图上绘制Student's t和标准普通pdf。 标准普通pdf（虚线）的尾部比学生氏 t pdf（实线）短。、

figure;

plot(x,y,'-',x,z,'-.')

四、F分布

定义

F分布的pdf为

其中Γ（•）是Gamma函数。

背景

F分布与卡方分布具有自然关系。 如果χ1和χ2分别是具有ν1和ν2自由度的卡方，则下面的统计量F是F分布。

 

两个参数ν1和ν2是分子和分母的自由度。 即，ν1和ν2分别是用于计算χ1和χ2的独立信息的数量。

例子   

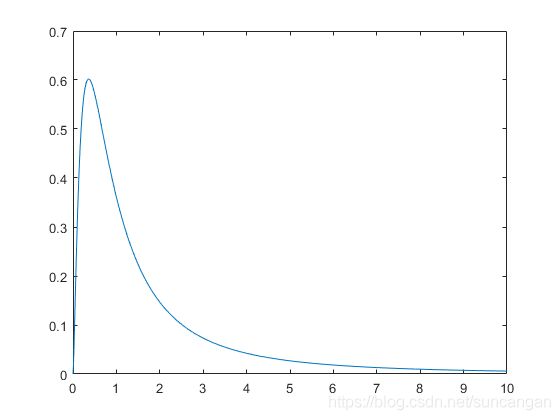
计算F分布pdf

计算具有5个分子自由度和3分母自由度的F分布的pdf。

x = 0:0.01:10;

y = fpdf(x,5,3);

figure;

plot(x,y)

该图显示F分布存在于正实数上并且向右倾斜。