模拟退火算法介绍-代码实现
1、爬山算法
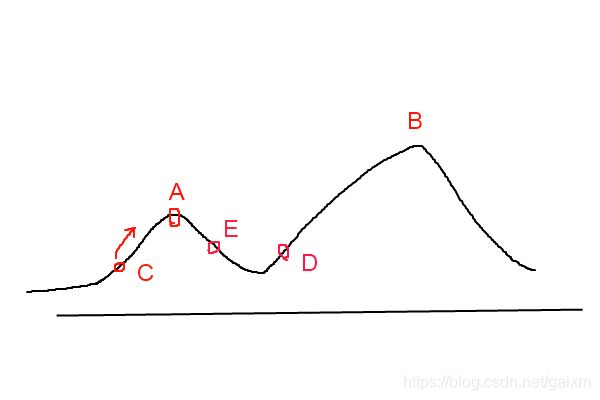
爬山算法是一种非常简单的贪心算法,它总是从当前解的邻近解中选择最优解作为当前解,直到达到局部最优解。爬山算法的算法过程如下图所示:
假设当前解从C点开始,经过若干次的邻近最优解搜索,到达了局部最优解A,此时A的邻近解中没有比当前解更优的,因此爬山算法到此结束,返回的最优解A。很明显,最优解应该是B点处的解,这便是爬山算法最大的弊端:极容易陷入局部最优。
2、模拟退火算法
由爬山算法可以得到一定的启发:如果在达到局部最优解时,程序能跳出局部最优,那就有极大的可能寻找到全局最优解。
模拟退火算法就是基于上述的思想,如果新解比当前解要差,那么就以一定的概率接受这个新解,这样就有可能跳出局部最优从而达到全局最优。以图1为例,当到达局部最优A点时,程序会以一定的概率移动到E点,再以一定的概率移动到D点,从而极有可能到达全局最优点B点。
模拟退火算法的步骤如下:
- 定义四个参数值:初始温度T,每个温度t的迭代次数L,温度衰退系数Dec(小于1),最低温度T_END
- 初始解状态S
- 在温度t下迭代步骤(4)至(6)L次
- 产生新的解S’
- 计算新解的效果值dX = f(S’) - f(S),其中f为结果值的计算函数。
- 如果dX<0,表示新解S’更优,则接受新解作为当前解,否则以概率exp(-dX/t)接受新解S’作为当前解
- 温度衰退,t = t * Dec
- 如果t>T_END,返回步骤3,否则程序终止,得到最终解。
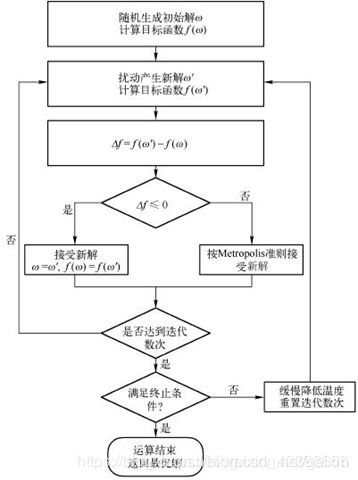
模拟退火算法的流程图如下所示:
3、模拟退火算法解决旅行商问题的实现
# -*- coding:utf-8 -*-
import math
import time
import random
# 初始温度值
T = 5000
# 结束温度值
T_end = 1e-8
# 在当前温度下的循环次数
L = 100
# 温度衰退系数
delta = 0.98
# 31个城市的坐标
citys = [[1304,2312],[3639,1315],[4177,2244],[3712,1399],[3488,1535],[3326,1556],[3238,1229],[4196,1004],[4312,790],[4386,570],[3007,1970],[2562,1756],[2788,1491],[2381,1676],[1332,695],[3715,1678],[3918,2179],[4061,2370],[3780,2212],[3676,2578],[4029,2838],[4263,2931],[3429,1908],[3507,2367],[3394,2643],[3439,3201],[2935,3240],[3140,3550],[2545,2357],[2778,2826],[2370,2975]]
# 存储城市间的距离
d = [[0 for i in range(31)] for j in range(31)]
# 最终的路径
ansPath = []
def getTwoCityDistance(i , j):
return math.sqrt((citys[i][0]-citys[j][0])**2 + (citys[i][1]-citys[j][1])**2)
def calcCityDistance():
n = len(citys)
for i in range(n):
for j in range(i , n):
d[i][j] = d[j][i] = getTwoCityDistance(i, j)
def getNewPath(oldPath):
i = random.randint(0, len(oldPath)-1)
j = random.randint(0, len(oldPath)-1)
oldPath[i], oldPath[j] = oldPath[j], oldPath[i]
return oldPath
def getPathDistance(path):
dist = 0
for i in range(len(path)-1):
dist += d[path[i]][path[i+1]]
return dist
# 是否采纳当前解
# 1、新值比旧值小
# 2、概率采纳
def metropolis(dOld, dNew, t):
de = dNew - dOld
if de<0:
return True
if (math.e**(-de/t)>random.random()):
return True
return False
def Saa():
delCnt = 0
calcCityDistance()
ansPath = range(0, len(citys))
t = T
result = 0
while t >= T_end:
for i in range(0, L):
newPath = getNewPath(ansPath)
dNew = getPathDistance(newPath)
dOld = getPathDistance(ansPath)
result = dOld
if (metropolis(dOld, dNew, t)==True):
result = dNew
ansPath = newPath
t *= delta
delCnt+=1
print("Path:")
print(ansPath)
print("PathDistance:")
print(result)
print("CoolDown Time:")
print(delCnt)
start = time.time()
Saa()
end = time.time()
print("Cost Time= %d s" % (end-start))
4、模拟退火算法的应用
模拟退火算法的应用很广泛,可以高效求解NP问题,如旅行者问题(TSP)、0-1背包问题、图着色问题等等。在实际应用中,主要需要控制以下三个参数,兼顾搜索空间与搜索效率的平衡:
- 初始温度值T。温度T的设置是影响退火算法全局搜索性能的重要因素。初始温度高,则搜索到全局最优解的可能性大,但要耗费较长的计算时间。
- 每个温度t下的迭代次数L,影响退火速度。同一温度下充分的搜索空间也是相当必要的,但是同时需要考虑到,L越大带来的计算时间消耗也就越多。
- 温度衰退问题。在实际应用中,一般采用公式t = t * dec进行温度衰退,dec小于1,并且最好接近1,且一般为0.98或0.95,为了保证较大的解空间。
参考链接:
https://www.cnblogs.com/sench/p/9427193.html
https://www.jianshu.com/p/f04fe7b58080