002C语言 验证无标度网络的幂律定律
1复杂网络发展史
几乎每个人都听说过大数学家欧拉和哥尼斯堡七桥的故事,而1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,也正式标志着数学的一个新的分支——图论与几何拓扑创建起来了。但此后很长一段时间,图论都没有什么重大的进展,直到本世纪,随着计算机科学的发展及仿真技术的进步,图论才开始焕发生机。从1959年随机图理论的提出(后来发现有很大的局限性),到1967年的小世界实验(比这个实验更闻名遐迩的是“六度分隔”理论),再到1973年,Granovertter发现并研究弱连接的强度,再到1998年Watts和Strogatz正式建立小世界模型,次年Barabasi和Albert又提出了无标度网络并发现了其幂律特性。不得不感叹,计算机在研究此类问题中的丰功伟绩!下面重点介绍一下无标度网络。
2无标度网络
随机图理论中,点的连接是随机的,这就造成了他很大的局限性,想想我们的现实世界中,某个领域中必然是功成名就者更容易被新接触这个领域的人认识,等等不胜枚举。无标度网络的先进之处就在于用两个特性深刻的刻画了生活中这种实际网络。无标度网络中,将实际网络概括为以下两个特性(大家可以好好品味以下)
A增长特性:即网络的规模是不断扩大的。例如每个月都会有新的科研文章发表,而万维网上每天都会产生大量新的网页。
B优先连接:即新的节点更倾向于与那些具有较高连接度的“大”节点相连接。这种现象也成为“富者更富”或“马太效应(Matthew Effect)”。例如新发表的文章更倾向于引用一些已经被广泛引用、有较高知名度的重要文献,新的个人主页上的超文本链接更有可能指向新浪、雅虎等著名站点。
解释一些关键概念:
连接度k:与该节点连接的其他节点的数量;
聚类系数C:与该节点相连的节点中实际连接的数目,与理论上最大连接数目的比值。
无标度网络的构造算法如下:
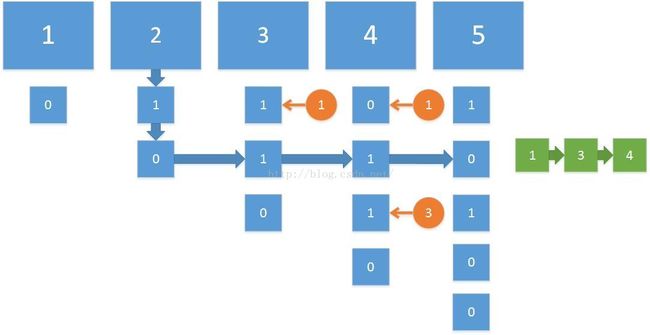
这里还要介绍一个邻接矩阵的概念,我这里实际上只使用了上三角部分。具体的构建思路在下面求k值部分有图示。
3编程实现
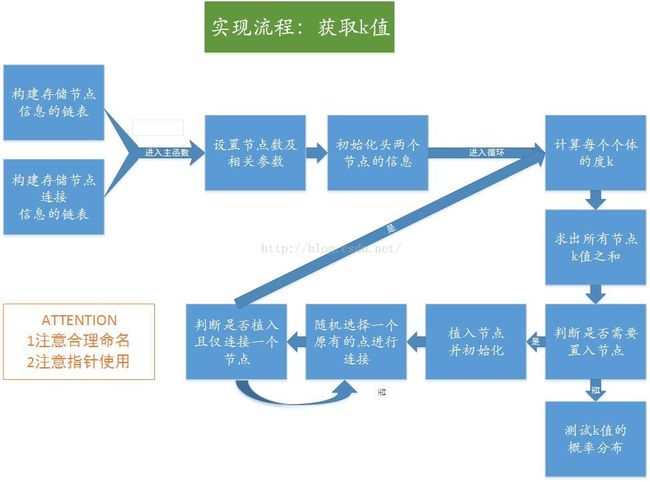
先祭出一张原理图
A、定义相关结构体及函数
#include
#include
#include
#include
int NumberofNodes = 0;
int NumberofBeginners = 0;
int NumberofLinks = 0;
typedef struct Node1
{
int Link;
struct Node1 *next_Adjacent;
}Adjacent;
typedef struct Node2
{
int Order;
int k;
double C;
Adjacent *Head;
struct Node2 *pre_Vertex;
struct Node2 *next_Vertex;
}Vertex;
typedef struct Node3
{
int k;
int k_SUM;
struct Node3 *next_List;
}k_List;
typedef struct Node4
{
int Order;
struct Node4 *next_List;
}C_List;
/************Introduction******************************/
void Introducction(void);
/************Set Parameter*****************************/
void SetParameter(void);
/************Initial***********************************/
Vertex *Initial(void);
/************EXAM**************************************/
void Exam(Vertex *pHead_Vertex)
{
long long k_TOTAL = 0;
Vertex *pNext_Vertex = NULL;
Adjacent *pNext_Adajcent = NULL;
pNext_Vertex = pHead_Vertex;
while(pNext_Vertex != NULL)
{
printf("%d\t", pNext_Vertex->k);
k_TOTAL += pNext_Vertex->k;
pNext_Vertex = pNext_Vertex->next_Vertex;
}
printf("k_TOTAL:%lld", k_TOTAL);
}
/************Add new Node***************************/
void AddNewNode(int Mark, Vertex *pHead_Vertex);
/************Caculate k***********************************/
void Caculate_k(Vertex *pHead_for_k);
/************Caculate P(k)***********************************/
void CaculatePofk(Vertex *pHead_Vertex);
/************Caculate C***********************************/
void CaculateC(Vertex *pHead_Vertex);
int main(void)
{
system("color 0A");
srand((unsigned)time(NULL));
Introducction();
SetParameter();
Vertex *pHead;//常量指针似乎更好
clock_t start, finish;
start = clock();
pHead = Initial();
printf("\nNow,add new node...\n");
for (int Temp2_i = NumberofBeginners+1; Temp2_i <= NumberofNodes; Temp2_i++)
AddNewNode(Temp2_i, pHead);
Caculate_k(pHead);
//Exam(pHead);
printf("\nCaculate the P for k\n");
CaculatePofk(pHead);
finish = clock();
printf("\nCaculate C\n");
CaculateC(pHead);
printf("\nsuccessful!\n");
if((double)(finish-start)/CLOCKS_PER_SEC > 180.0)
printf("\nTime used:%4.2fmin", ((double)(finish-start)/CLOCKS_PER_SEC)/60.0);
else
printf("\nTime used:%4.2fs", ((double)(finish-start)/CLOCKS_PER_SEC));
getchar();
return 0;
}void Introducction(void)
{
system("cls");
printf("\t\t*******Scale-free Network*******\n\t\t\t\t\t\t\tMade By Zhao Yu\n");
printf("\tYou can find lots of introduction about scale-free network via internet.");
printf("In this program,you will input three parameters to create a scale-free network,");
printf("by which we can prove the power law distribution.");
printf("At first,you will input NumberofNodes which means the quantity of nodes in the end;");
printf("then you will input NumberofBeginners which means the quantity of nodes at the beginning;");
printf("at last,you will input NumberofLinks which means the quantity of new links when add a new node.");
printf("What you should pay attention to is that NumberofBeginners<=NumberofNodes、");
printf("NumberofLinks<=NumberofBeginners,or you will input again");
printf("\nThat\'s all!\nenter to next step!");
getchar();
}void SetParameter(void)
{//健壮性不行
system("cls");
printf("\t\t*******Scale-free Network*******\n\t\t\t\t\t\t\tMade By Zhao Yu\n\n");
printf("Input number of nodes:");
scanf("%d", &NumberofNodes);
printf("\ninput number of beginners(<=%d):",NumberofNodes);
do{
scanf("%d", &NumberofBeginners);
}while(NumberofBeginners>NumberofNodes);
printf("\nInput number of new links for every new node(<=%d):", NumberofBeginners);
do{
scanf("%d", &NumberofLinks);
}while(NumberofLinks>NumberofBeginners);
printf("\nOK!enter to next step.");
getchar();
getchar();
}Vertex *Initial(void)
{
Vertex *pHead_Vertex = NULL;
Vertex *pNext_Vertex = NULL;
Vertex *pTail_Vertex = NULL;
Adjacent *pHead_Adajcent = NULL;
Adjacent *pNext_Adajcent = NULL;
Adjacent *pTail_Adajcent = NULL;
pHead_Vertex = (Vertex *)malloc(sizeof(Vertex));
pHead_Vertex->Order = 1;
pNext_Vertex = pHead_Vertex;
pNext_Vertex->next_Vertex = NULL;
printf("\nCreate beginners...\n");
//创建NumberofBeginners个节点
for (int i = 2; i <= NumberofBeginners; i++)
{
pTail_Vertex = (Vertex *)malloc(sizeof(Vertex));
pTail_Vertex->Order = i;
pTail_Vertex->next_Vertex = NULL;
pNext_Vertex->next_Vertex = pTail_Vertex;
pNext_Vertex = pTail_Vertex;
}
pNext_Vertex = pHead_Vertex;
while(pNext_Vertex != NULL)
{
pHead_Adajcent = (Adjacent *)malloc(sizeof(Adjacent));
pNext_Vertex->Head = pHead_Adajcent;
pNext_Adajcent = pHead_Adajcent;
pNext_Adajcent->next_Adjacent = NULL;
for (int Temp_i = 1; Temp_i <= pNext_Vertex->Order; Temp_i++)
{
if (Temp_i == pNext_Vertex->Order)
pNext_Adajcent->Link = 0;
else
pNext_Adajcent->Link = 1;
if (Temp_i < pNext_Vertex->Order)
{
pTail_Adajcent = (Adjacent *)malloc(sizeof(Adjacent));
pTail_Adajcent->next_Adjacent = NULL;
pNext_Adajcent->next_Adjacent = pTail_Adajcent;
pNext_Adajcent = pTail_Adajcent;
}
else
break;
}
pNext_Vertex = pNext_Vertex->next_Vertex;
}
Caculate_k(pHead_Vertex);
return pHead_Vertex;
}F、计算k值函数(比较复杂)
void Caculate_k(Vertex *pHead_for_k)
{
Vertex *pMove = NULL;
Vertex *pNext_Vertex = NULL;
Adjacent *pNext_Adajcent = NULL;
pNext_Vertex = pHead_for_k;
while (pNext_Vertex != NULL)
{
pNext_Vertex->k = 0;
pMove = pNext_Vertex;
while (pMove != NULL)
{
if (pMove == pNext_Vertex)
{
pNext_Adajcent = pNext_Vertex->Head;
while (pNext_Adajcent != NULL)
{
pNext_Vertex->k += pNext_Adajcent->Link;
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
}
pMove = pMove->next_Vertex;
}
else
{
pNext_Adajcent = pMove->Head;
int Temp1_i = 1;
while (pNext_Adajcent != NULL)
{
if (Temp1_i == pNext_Vertex->Order)
{
pNext_Vertex->k += pNext_Adajcent->Link;
break;
}
else
{
Temp1_i++;
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
}
}
pMove = pMove->next_Vertex;
}
}
pNext_Vertex = pNext_Vertex->next_Vertex;
}
}void AddNewNode(int Mark, Vertex *pHead_Vertex)
{
//Caculate k
Caculate_k(pHead_Vertex);
//caculate sum of k
Vertex *pNext_Vertex = NULL;
long long k_TOTAL = 0;
pNext_Vertex = pHead_Vertex;
while (pNext_Vertex != NULL)
{
k_TOTAL += pNext_Vertex->k;
pNext_Vertex = pNext_Vertex->next_Vertex;
}
//add node
Vertex *pTail_Vertex = NULL;
pTail_Vertex = (Vertex *)malloc(sizeof(Vertex));
pTail_Vertex->Order = Mark;
pTail_Vertex->next_Vertex = NULL;
pNext_Vertex = pHead_Vertex;
while (pNext_Vertex->next_Vertex != NULL)
pNext_Vertex = pNext_Vertex->next_Vertex;
pNext_Vertex->next_Vertex = pTail_Vertex;
Adjacent *pNext_Adajcent = NULL;
Adjacent *pTail_Adajcent = NULL;
pNext_Adajcent = (Adjacent *)malloc(sizeof(Adjacent));
pNext_Adajcent->Link = 0;
pNext_Adajcent->next_Adjacent = NULL;
pTail_Vertex->Head = pNext_Adajcent;
for (int Temp3_i = 2; Temp3_i <= pTail_Vertex->Order; Temp3_i++)
{
pTail_Adajcent = (Adjacent *)malloc(sizeof(Adjacent));
pTail_Adajcent->Link = 0;
pTail_Adajcent->next_Adjacent = NULL;
pNext_Adajcent->next_Adjacent = pTail_Adajcent;
pNext_Adajcent = pTail_Adajcent;
}
//选择NumberofLinks个连接点
pTail_Vertex = pHead_Vertex;
while (pTail_Vertex->next_Vertex != NULL)
pTail_Vertex = pTail_Vertex->next_Vertex;
int Judge = NumberofLinks;
while (Judge)
{
int RandomNumber = rand()%(Mark-1) + 1;
for (int Temp4_i = 1; Temp4_i < Mark; Temp4_i++)
{
if(RandomNumber == Temp4_i)
{
pNext_Adajcent = pTail_Vertex->Head;
for (int Temp5_i = 1; Temp5_i < RandomNumber; Temp5_i++)
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
if(pNext_Adajcent->Link == 1)
break;//自习考虑这个break的影响
else
{
double RandomNum = (double)rand()/RAND_MAX;
double Probality = (double)pNext_Vertex->k/k_TOTAL;
if(RandomNum < Probality)
{Caculate_k(pHead_Vertex);
pNext_Adajcent->Link = 1;
Judge--;
}
}
}
}
}
}
void CaculatePofk(Vertex *pHead_Vertex)
{
//Range of k
k_List *pHead_k = (k_List *)malloc(sizeof(k_List));
pHead_k->k = pHead_Vertex->k;
pHead_k->k_SUM = 1;
pHead_k->next_List = NULL;
k_List *pNext_k = pHead_k;
k_List *pTail_k = NULL;
//count k
Vertex *pNext_Vertex = pHead_Vertex->next_Vertex;
while(pNext_Vertex != NULL)
{
int Judge = 1;
pNext_k = pHead_k;
while(pNext_k != NULL)
{
if (pNext_k->k == pNext_Vertex->k)
{
pNext_k->k_SUM++;
Judge = 0;
break;
}
pNext_k = pNext_k->next_List;
}
if(Judge)
{
pTail_k = (k_List *)malloc(sizeof(k_List));
pTail_k->k = pNext_Vertex->k;
pTail_k->k_SUM = 1;
pTail_k->next_List = NULL;
pNext_k = pHead_k;
while(pNext_k->next_List != NULL)
{
pNext_k = pNext_k->next_List;
}
pNext_k->next_List = pTail_k;
}
pNext_Vertex = pNext_Vertex->next_Vertex;
}
FILE *fp = fopen("DATA.txt", "w");
pNext_k = pHead_k;
while (pNext_k != NULL)
{
fprintf(fp, "%d\t%f\n", pNext_k->k, (double)pNext_k->k_SUM/NumberofNodes);
pNext_k = pNext_k->next_List;
}
free(fp);
}void CaculateC(Vertex *pHead_Vertex)
{
Vertex *pNext_Vertex = NULL;
Vertex *pMove_Vertex = NULL;
Vertex *pMove_Vertex_Temp = NULL;
Adjacent *pNext_Adajcent = NULL;
C_List *pHead_C_List = (C_List *)malloc(sizeof(C_List));
pHead_C_List->Order = 0;
pHead_C_List->next_List = NULL;
C_List *pNext_C_List = NULL;
C_List *pMove_C_List = NULL;
C_List *pTail_C_List = NULL;
FILE *fp = fopen("C.txt", "w");
double TotalC = 0;
//构建双向链表
pHead_Vertex->pre_Vertex = NULL;
pMove_Vertex = pNext_Vertex = pHead_Vertex;
while (1)
{
pNext_Vertex = pNext_Vertex->next_Vertex;
if(pNext_Vertex == NULL)
break;
pNext_Vertex->pre_Vertex = pMove_Vertex;
pMove_Vertex = pNext_Vertex;
}
pNext_Vertex = pHead_Vertex;
while (pNext_Vertex != NULL)
{
int CountLink = 0;
pNext_C_List = pHead_C_List;
pMove_Vertex = pNext_Vertex;
while (pMove_Vertex != NULL)
{
if(pMove_Vertex == pNext_Vertex)
{
pNext_Adajcent = pNext_Vertex->Head;
int Temp6_i = 1;
while (pNext_Adajcent != NULL)
{
if(pNext_Adajcent->Link == 1)
{
CountLink++;
pTail_C_List = (C_List *)malloc(sizeof(C_List));
pTail_C_List->Order = Temp6_i;
pTail_C_List->next_List = NULL;
pNext_C_List->next_List = pTail_C_List;
pNext_C_List = pTail_C_List;
}
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
Temp6_i++;
}
}
else
{
pNext_Adajcent = pMove_Vertex->Head;
int Temp7_i = 1;
while (pNext_Adajcent != NULL)
{
if (Temp7_i == pNext_Vertex->Order)
break;
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
Temp7_i++;
}
if(pNext_Adajcent->Link == 1)
{
CountLink++;
pTail_C_List = (C_List *)malloc(sizeof(C_List));
pTail_C_List->Order = pMove_Vertex->Order;
pTail_C_List->next_List = NULL;
pNext_C_List->next_List = pTail_C_List;
pNext_C_List = pTail_C_List;
}
}
pMove_Vertex = pMove_Vertex->next_Vertex;
}
pNext_C_List = pHead_C_List->next_List;
//计算实际相连
int ActualLink = 0;
pMove_Vertex = pHead_Vertex;
while (pMove_Vertex->next_Vertex != NULL)
pMove_Vertex = pMove_Vertex->next_Vertex;
while (pMove_Vertex != NULL)
{
pMove_C_List = pHead_C_List->next_List;
while(pMove_C_List != NULL)
{
if(pMove_Vertex->Order == pMove_C_List->Order)
{
pNext_C_List = pHead_C_List->next_List;
pNext_Adajcent = pMove_Vertex->Head;
int Temp8_i = 1;
while (pNext_Adajcent != NULL)
{
pNext_C_List = pHead_C_List->next_List;
while (pNext_C_List != NULL)
{
if(pNext_C_List->Order == Temp8_i)
{
if (pNext_Adajcent->Link == 1)
ActualLink++;
}
pNext_C_List = pNext_C_List->next_List;
}
pNext_Adajcent = pNext_Adajcent->next_Adjacent;
Temp8_i++;
}
}
pMove_C_List = pMove_C_List->next_List;
}
pMove_Vertex = pMove_Vertex->pre_Vertex;
}
pNext_Vertex->C = (double)ActualLink/CountLink;
fprintf(fp, "%f\n", pNext_Vertex->C);
TotalC += pNext_Vertex->C;
pNext_Vertex = pNext_Vertex->next_Vertex;
}
printf("\nAverage of all vertice is:%f\n", TotalC/NumberofNodes);
}
获取聚类系数的思路图示
4、界面展示
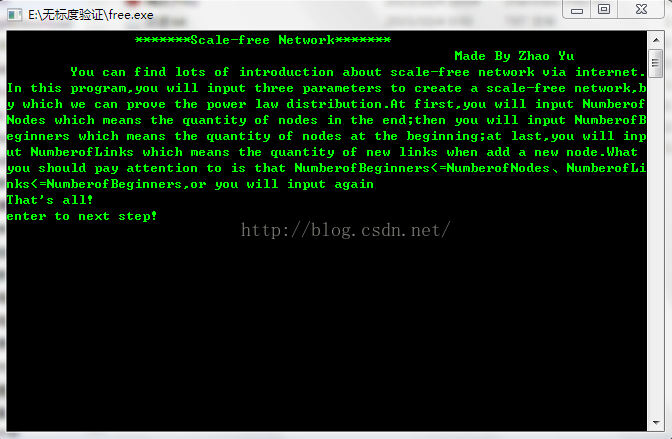
Part1:启动exe后会提示一些基本信息
Part2:回车键后会提示输入三个参数(最后的节点数、开始的节点数、每增加一个新节点连接的原有节点数)
运行结束后会输出文本以及运行时间等参数,如果输入不合理不会想下执行。
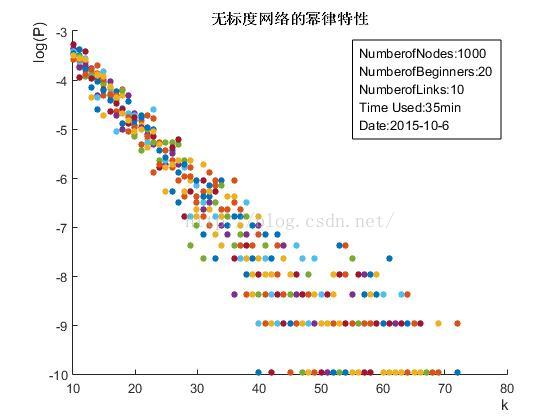
Part3:在总结点1000,初始节点20,每个新节点连接10个原有节点时,通过matlab作散点图如下图
将P(k)取对数得到
可以看到,确实是一条直线,至此幂律特性得到验证。
5缺点分析
1命名还是相当混乱
2方法复杂,100个时只要0.06s但是1000个时就要35min左右了,说明时间复杂度还是相当高的;
3指针使用混乱,应该很多指针该释放的
4节点数太多(>1000)时效率太低,耗时简直指数级增加
5第一次写技术博客,发现把自己的思路表达清楚真不是那么容易,写的估计一般人都看不懂!
6无标度网络的其他一些特性没有时间恐怕现在也没有能力来实现。
7是不是有更好的可视化方法表现无标度网络的各种特性。
6收获
1通过置入printf()发现运行时指针错误的位置,而不是直接分析,节省时间;
2更加坚定了自己要学习数据结构的决心;
3把原来的代码重写一遍,发现命名规范了不少,思路也清晰了不少,所以不要嫌浪费时间,重写代码还是很有用的;
4控制好写代码和思考的比例,对于k值的计算,在构思好后再写真是顺利了不少,控制好学习新知识和敲代码的时间比例。
5晚上不适合写太难的东西
6很多辅助软件要熟练掌握,Matlab太强大太重要了,Visio代替画板画原理图也节省了我不少时间,XMind用的很不顺手,但是Visio自己还远远没有掌握。
7现在学的太少了,用C语言操作指针真是个费脑子的活,直接用matlab编会不会更简单一些,或者用C++的一些方法,可惜现在自己就C语言会一点,C语言也有很多东西没学到。
8一定要学好数据结构和算法,总是自己设计毕竟是有局限性的。
7参考
1《复杂网络及其应用》 王小帆 李翔 陈关荣 清华出版社
2