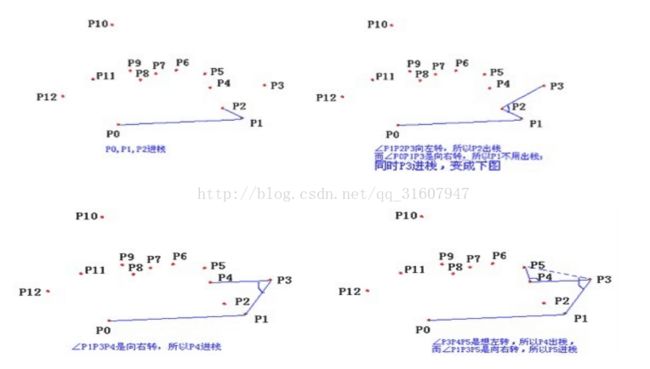
hdu1392凸包.叉乘
基于水平序的Andrew 算法
先说叉乘,
double Multiply(POINT p1 , POINT p2 , POINT p3)
{
return ( (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x) ) ;
}
对于空间的两点:
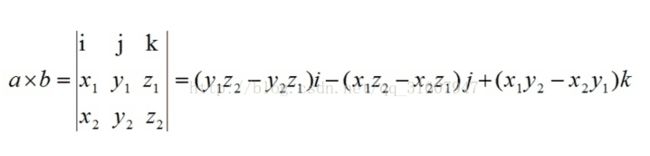
叉乘几何意义:
在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。
在二维空间中(k下面为0),叉乘还有另外一个几何意义就是:aXb等于由向量a和向量b构成的平行四边形的面积。在这道题中先用y确定一个最底部的点p0(同时还要是最左边)
然后对于其余的点排序
排序的依据就是叉乘
int cmp ( const void *p1 , const void *p2 )
{
POINT *p3,*p4;
double m;
p3 = (POINT *)p1;
p4 = (POINT *)p2;
m = Multiply(tree[0] , *p3 , *p4) ;
if(m < 0) return 1;
else if(m == 0 && (Distance(tree[0] , *p3) < Distance(tree[0],*p4))) //同一条线上的两个点取离p0远的
return 1;
else return -1;
}
对于三个点p0,p1,p2,为1时P1在P2顺时针方向
叉乘的作用是为除p0外的两个点进行排序
又捕获了一个cmp,然而还是懵懵懂懂
排好序后,继续还是利用叉乘
void Tubao ()
{
int i ;
result[0].x = tree[0].x;
result[0].y = tree[0].y;
result[1].x = tree[1].x;
result[1].y = tree[1].y;
result[2].x = tree[2].x;
result[2].y = tree[2].y;
top = 2;
for ( i = 3 ; i <= n ; ++ i )
{
while (Multiply(result[top - 1] , result[top] , tree[i]) <= 0 )
top -- ; //出栈
result[top + 1].x = tree[i].x ;
result[top + 1].y = tree[i].y ;
top ++ ;
}
}
这个图还是挺生动的,
我有点懵左转右转
差不多这样了
md忘了教学楼要关门要被门岗阿姨骂了
#include
#include
#include
typedef struct
{
double x , y ;
} POINT ;
POINT result[110] ;// 模拟堆栈S,保存凸包上的点
POINT tree[110] ;
int n , top ;
double Distance ( POINT p1 , POINT p2 )
{
return sqrt( (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y) ) ;
}
double Multiply(POINT p1 , POINT p2 , POINT p3) // 叉积
{
return ( (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x) ) ;
}
int cmp ( const void *p1 , const void *p2 )
{
POINT *p3,*p4;
double m;
p3 = (POINT *)p1;
p4 = (POINT *)p2;
m = Multiply(tree[0] , *p3 , *p4) ;
if(m < 0) return 1;
else if(m == 0 && (Distance(tree[0] , *p3) < Distance(tree[0],*p4)))
return 1;
else return -1;
}
void Tubao ()
{
int i ;
result[0].x = tree[0].x;
result[0].y = tree[0].y;
result[1].x = tree[1].x;
result[1].y = tree[1].y;
result[2].x = tree[2].x;
result[2].y = tree[2].y;
top = 2;
for ( i = 3 ; i <= n ; ++ i )
{
while (Multiply(result[top - 1] , result[top] , tree[i]) <= 0 )
top -- ; //出栈
result[top + 1].x = tree[i].x ;
result[top + 1].y = tree[i].y ;
top ++ ;
}
}
int main ()
{
int pos ;
double len , temp , px , py ;
while ( scanf ( "%d" , &n ) != EOF , n )
{
py = -1 ;
for ( int i = 0 ; i < n ; ++ i )
{
scanf ( "%lf%lf" , &tree[i].x , &tree[i].y ) ;
}
if ( n == 1 )
{
printf ( "0.00\n" ) ;
continue ;
}
else if ( n == 2 )
{
printf ( "%.2lf\n" , Distance(tree[0] , tree[1]) ) ;
continue ;
}
for ( int i = 0 ; i < n ; ++ i )
{
if(py == -1 || tree[i].y < py)
{
px = tree[i].x;
py = tree[i].y;
pos = i;
}
else if(tree[i].y == py && tree[i].x < px)
{
px = tree[i].x;
py = tree[i].y;
pos = i;
}
}
temp = tree[0].x ; // 找出y最小的点
tree[0].x = tree[pos].x ;
tree[pos].x = temp ;
temp = tree[0].y ;
tree[0].y = tree[pos].y ;
tree[pos].y = temp ;
qsort(&tree[1],n - 1,sizeof(double) * 2,cmp);
tree[n].x = tree[0].x;
tree[n].y = tree[0].y;
Tubao();
len = 0.0;
for(int i = 0 ; i < top ; i ++)
len = len + Distance(result[i] , result[i+1]) ;
printf("%.2lf\n",len);
}
return 0 ;
}
部分来自博客园的贺佐安的计算几何-经典算法-凸包
/************************************************************************************************************************************/
另外一种方法不需要排序,但是运算量比较大(提交的时候超时了)
for(i=1;i<=n;i++)
if(p[i].y < p[t].y)
t = i;
pl[1] = t;
先放入一个最底部的点
然后
int num = 1; //凸包点的数量
do{ //已确定凸包上num个点
num++; //该确定第 num+1 个点了
t = pl[num-1]+1;
if(t>n) t = 1;
for(int i=1;i<=n;i++){ //核心代码。根据叉积确定凸包下一个点。
double x = xmulti(p[i],p[t],p[pl[num-1]]);
if(x<0) t = i;
}
pl[num] = t;
} while(pl[num]!=pl[1]);
当x<0 时使用i点,遍历n个点后此时t代表的点为上一个点最右边的点,将这个点t放入pl中,继续遍历
这种方法比较简单,不过可以预见的是费时
#include
#include
#include
using namespace std;
struct Point{
double x,y;
}p[105],pl[105];
double dis(Point p1,Point p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
double xmulti(Point p1,Point p2,Point p0) //求p1p0和p2p0的叉积,如果大于0,则p1在p2的顺时针方向
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double graham(Point p[],int n) //点集和点的个数
{
int pl[105];
//找到纵坐标(y)最小的那个点,作第一个点
int i;
int t = 1;
for(i=1;i<=n;i++)
if(p[i].y < p[t].y)
t = i;
pl[1] = t;
//顺时针找到凸包点的顺序,记录在 int pl[]
int num = 1; //凸包点的数量
do{ //已确定凸包上num个点
num++; //该确定第 num+1 个点了
t = pl[num-1]+1;
if(t>n) t = 1;
for(int i=1;i<=n;i++){ //核心代码。根据叉积确定凸包下一个点。
double x = xmulti(p[i],p[t],p[pl[num-1]]);
if(x<0) t = i;
}
pl[num] = t;
} while(pl[num]!=pl[1]);
//计算凸包周长
double sum = 0;
for(i=1;i
return sum;
}
int main()
{
int n;
while(cin>>n){
if(n==0) break;
int i;
for(i=1;i<=n;i++)
cin>>p[i].x>>p[i].y;
if(n==1){
cout<<0<
}
if(n==2){
cout<
}
cout<
return 0;
}