Looploop Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2054 Accepted Submission(s): 675
Problem Description
XXX gets a new toy named Looploop. The toy has N elements arranged in a loop, an arrow pointing to one of the elements, and two preset parameters k1 and k2. Every element has a number on it.
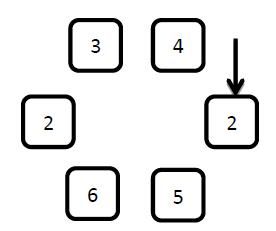
The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy.
1: add x
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.
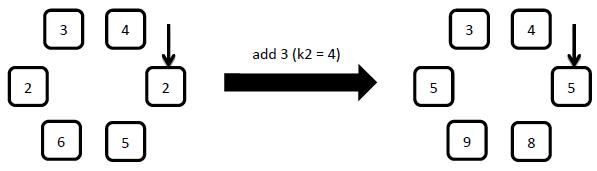
2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.
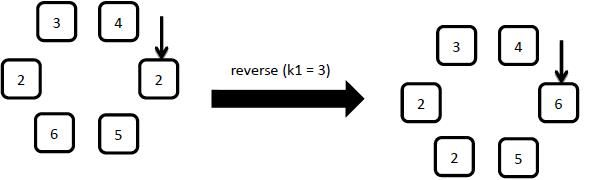
3: insert x
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.
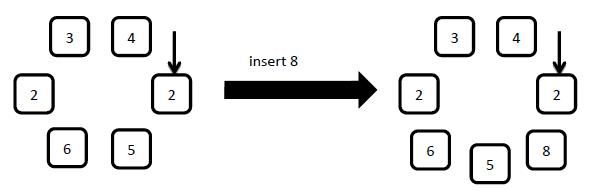
4: delete
Delete the element the arrow pointed and then move the arrow to the right element.
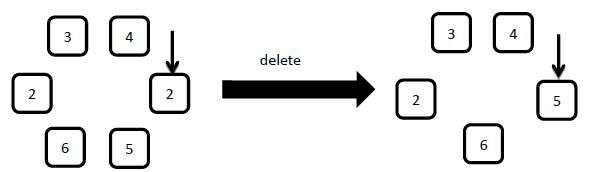
5: move x
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.
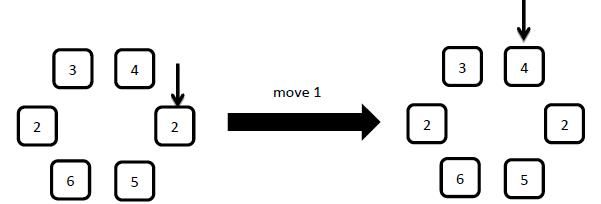
6: query
Output the number on the arrow pointed element in one line.
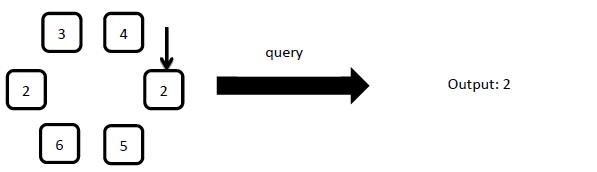
XXX wants to give answers to every query in a serial of operations.
Input
There are multiple test cases.
For each test case the first line contains N,M,k1,k2(2≤k15, M≤10
5) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy.
Second line contains N integers ai(-10
4≤ai≤10
4) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning.
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations.
The input ends with a line of 0 0 0 0.
Output
For each test case, output case number in the first line(formatted as the sample output). Then for each query in the case, output the number on the arrow pointed element in a single line.
Sample Input
5 1 2 4 3 4 5 6 7 query 5 13 2 4 1 2 3 4 5 move 2 query insert 8 reverse query add 2 query move 1 query move 1 query delete query 0 0 0 0
Sample Output
Case #1: 3 Case #2: 2 8 10 1 5 1
Source
2012 Asia Hangzhou Regional Contest
以这个序列为基准建一颗伸展树,在序列头尾分别加上一个虚拟节点。用pos表示指针的位置,初始为1。
1. Move操作。这个最简单,只需把pos变成pos+1或pos-1即可,注意1->n和n->1的转变。
2. Query操作。把pos所指的节点转到根节点,根节点的值就是答案
3. Insert 操作。可以把区间[1, pos](这里没有算上虚拟节点,以下也是)转到根节点,把区间[pos+1, n]转到根节点右儿 子,那么根节点左儿子现在为空,放入要插入的点即可。
4. Delete操作。可以把区间[1, pos-1]转到根节点,把区间[pos+1,n]转到根节点右儿子,那么此时根节点左儿子即为要删 除的节点。
5.Add或Reverse操作。因为我们的序列是线型的,而这里的操作是相对环形区间来的,所以可能出现pos+k1大于n或pos+k2大于n的情况。为了避免这种情况,我们可以将pos变为1,即指向最前面的元素。方法是将区间[1, pos-1]拆下来放到序列尾部。这个操作进行之后就是普通的区间修改操作了。
#include
#include
#include
#include
//对区间操作
#define Key_value ch[ch[root][1]][0]
using namespace std;
const int maxn = 4e5 + 10;
int root, tot1;
int ch[maxn][2], pre[maxn], key[maxn], size[maxn], add[maxn], rev[maxn];
int s[maxn], tot2;
int n, q, k1, k2, pos, a[maxn];
void Update_Add(int r, int v)
{
if(!r) return;
key[r] += v;
add[r] += v;
}
void Update_Rev(int r)
{
if(!r) return;
swap(ch[r][0], ch[r][1]);
rev[r] ^= 1;
}
void PushUp(int r)
{
size[r] = size[ch[r][0]] + size[ch[r][1]] + 1;
}
void PushDown(int r)
{
if(add[r])
{
Update_Add(ch[r][0], add[r]);
Update_Add(ch[r][1], add[r]);
add[r] = 0;
}
if(rev[r])
{
Update_Rev(ch[r][0]);
Update_Rev(ch[r][1]);
rev[r] = 0;
}
}
void NewNode(int &r, int fa, int v)
{
if(tot2) r = s[tot2--];
else r = ++tot1;
ch[r][0] = ch[r][1] = add[r] = 0;
size[r] = 1;
pre[r] = fa;
key[r] = v;
rev[r] = 0;
add[r] = 0;
}
void Build(int &x, int fa, int l, int r)
{
if(l > r) return;
int mid = (l + r) >> 1;
NewNode(x, fa, a[mid]);
Build(ch[x][0], x, l, mid-1);
Build(ch[x][1], x, mid+1, r);
PushUp(x);
}
void Init()
{
pos = 1;
root = tot1 = tot2 = 0;
add[root] = ch[root][0] = ch[root][1] = pre[root] = key[root] = size[root] = 0;
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
//放两个虚拟节点
NewNode(root, 0, -1);
NewNode(ch[root][1], root, -1);
//建树
Build(Key_value, ch[root][1], 1, n);
PushUp(ch[root][1]);
PushUp(root);
}
void Rotate(int x, int kind)
{
int y = pre[x];
PushDown(y);
PushDown(x);
ch[y][!kind] = ch[x][kind];
pre[ch[x][kind]] = y;
if(pre[y])
ch[pre[y]][ch[pre[y]][1]==y] = x;
pre[x] = pre[y];
ch[x][kind] = y;
pre[y] = x;
PushUp(y);
}
void Splay(int r, int goal)
{
PushDown(r);
while(pre[r] != goal)
{
if(pre[pre[r]] == goal)
{
Rotate(r, ch[pre[r]][0]==r);
}
else
{
int y = pre[r];
int kind = (ch[pre[y]][0]==y);
if(ch[y][kind] == r)
{
Rotate(r, !kind);
Rotate(r, kind);
}
else
{
Rotate(y, kind);
Rotate(r, kind);
}
}
}
PushUp(r);
if(goal == 0) root = r;
}
int Get_Max(int r)
{
PushDown(r);
while(ch[r][1])
{
r = ch[r][1];
PushDown(r);
}
return r;
}
//得到序列第k个元素
int Kth(int r, int k)
{
PushDown(r);
int t = size[ch[r][0]] + 1;
if(k == t) return r;
else if(k < t) return Kth(ch[r][0], k);
else return Kth(ch[r][1], k - t);
}
//将区间[l, r]放到尾部
void MoveLast(int l, int r)
{
if(l > r) return;
//首先将区间[l,r]旋转到root下面,并切割出来。
Splay(Kth(root, l), 0);
Splay(Kth(root, r+2), root);
int rt = Key_value;
Key_value = 0;
PushUp(ch[root][1]);
PushUp(root);
//找到剩余区间中最后一个元素(注意:因为最后有个虚拟节点,所以这里取的是最后的虚拟节点)
Splay(Get_Max(root), 0);
int rtt = root;
root = ch[root][0]; //把这个虚拟节点从原序列中删除
pre[root] = 0;
PushUp(root);
//再找剩余区间中最后一个元素(这个就是真正的序列末元素了),并将区间[l,r]接到其后面
Splay(Get_Max(root), 0);
ch[root][1] = rt;
pre[rt] = root;
PushUp(root);
//把删掉的虚拟节点加上
ch[rtt][0] = root;
pre[root] = rtt;
root = rtt;
pre[root] = 0;
PushUp(root);
}
void Insert(int x)
{
int r;
Splay(Kth(root, pos+1), 0);
Splay(Kth(root, pos+2), root);
NewNode(r, ch[root][1], x);
Key_value = r;
PushUp(ch[root][1]);
PushUp(root);
++n;
}
void erase(int r)
{
if(!r) return;
erase(ch[r][0]);
erase(ch[r][1]);
s[++tot2] = r;
}
void Delete()
{
//这两步将第pos元素转到ch[root][1]下面
Splay(Kth(root, pos), 0);
Splay(Kth(root, pos+2), root);
int r = Key_value;
Key_value = 0;
pre[r] = 0;
erase(r);
PushUp(ch[root][1]);
PushUp(root);
if(pos == n) pos = 1;
--n;
}
void Move(int x)
{
if(x == 1) pos = (pos > 1 ? pos-1 : n);
else pos = (pos < n ? pos+1 : 1);
}
int Query()
{
Splay(Kth(root, pos+1), 0);
return key[root];
}
void Add(int x)
{
MoveLast(1, pos-1);
pos = 1;
int l = pos, r = pos + k2 - 1;
Splay(Kth(root, l), 0);
Splay(Kth(root, r+2), root);
Update_Add(Key_value, x);
}
void Reverse()
{
MoveLast(1, pos-1);
pos = 1;
int l = pos, r = pos + k1 - 1;
Splay(Kth(root, l), 0);
Splay(Kth(root, r+2), root);
Update_Rev(Key_value);
}
int main()
{
int kase = 0;
while(scanf("%d%d%d%d", &n, &q, &k1, &k2) == 4)
{
if(!n && !q && !k1 && !k2) break;
char op[10];
int x;
Init();
printf("Case #%d:\n", ++kase);
for(int i = 1; i <= q; i++)
{
scanf("%s", op);
if(op[0] == 'a')
{
scanf("%d", &x);
Add(x);
}
else if(op[0] == 'r') Reverse();
else if(op[0] == 'i')
{
scanf("%d", &x);
Insert(x);
}
else if(op[0] == 'd') Delete();
else if(op[0] == 'm')
{
scanf("%d", &x);
Move(x);
}
else if(op[0] == 'q') printf("%d\n", Query());
}
}
return 0;
}
|