计算几何2- 判断两线段是否相交

前置知识：向量叉积

给你两个向量 $a=(x_1,y_1)$ 与 $b=(x_2,y_2)$
我们定义他们的叉积
$$a\times b=x_1\times y_2-x_2\times y_1$$
那么有啥子实际意义呢？

1. 叉积的正负：
   若 $a\times b<0$，表示$b$在向量$a$的顺时针方向
   若 $a\times b>0$，表示$b$在向量$a$的逆时针方向
   若 $a\times b=0$, 表示向量a与向量b平行。
2. 叉积的绝对值
   $|a\times b|$的值是以$a$,$b$为临边的平行四边形面积
   当然，你想要三角形面积除2就可以了

判断相交两个阶段

快速排斥(跨立)试验

设以线段 $P_1{P}_2$ 为对角线的矩形为R， 设以线段 $Q_1{Q}_2$ 为对角线的矩形为T，如果R和T不相交，显然两线段不会相交。

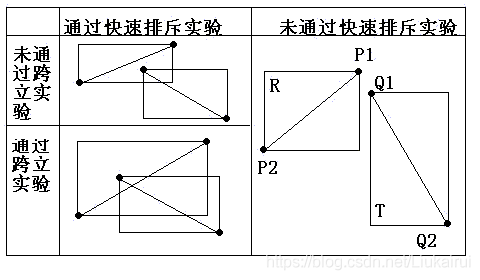
轻松写出快速跨立实验代码

struct point{
    double x,y;
};

struct vec{
    point st,ed;
}a,b;

double cj(point a,point b,point c){
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

bool jduge(vec p,vec q){
    if(min(p.st.x,p.ed.x)>max(q.st.x,q.ed.x))return false;
    if(min(p.st.y,p.ed.y)>max(q.st.y,q.ed.y))return false;
    if(min(q.st.x,q.ed.x)>max(p.st.x,p.ed.x))return false;
    if(min(q.st.y,q.ed.y)>max(p.st.y,p.ed.y))return false;
    return true;
}

叉积判断

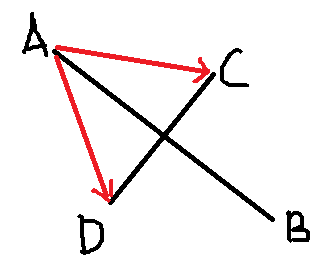
在上图中，线段AB与线段CD相交，于是我们可以得到两个向量AC，AD，C和D分别在AB的两边，向量AC在向量AB的逆势针方向，AB×AC > 0；向量AD在向量AB的顺势针方向，AB×AD < 0，两叉乘结果异号。
这样，方法就出来了：如果线段CD的两个端点C和D，与另一条线段的一个端点（A或B，只能是其中一个）连成的向量，与向量AB做叉乘，若结果异号，表示C和D分别在直线AB的两边，若结果同号，则表示CD两点都在AB的一边，则肯定不相交。
当然，不能只证明C，D在直线AB的两边，还要用相同的方法证明A，B在直线CD的两边，两者同时满足才是线段相交的充要条件。
不过，线段相交还有一些特殊情况：

1.只有1点相交，如下图

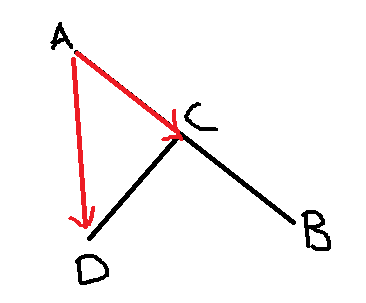
上图中，线段AB与CD相交于C点，按照之前介绍的方法，我们可以连成两向量AD和AC，这时候，我们发现，AC与AB共线，AB×AC = 0；而AB×AD < 0；两者并不异号，可实际上仍然相交。所以当出现两叉乘结果中，有一方为0，也可以看成点CD在直线AB的两边。

2.两条线段重合，如下图：

对于这两种情况只要微微修改向量叉积代码就可以实现

if(cj(p.st,q.st,p.ed)*cj(p.st,p.ed,q.ed)<0)return false;
if(cj(q.st,p.st,q.ed)*cj(q.st,q.ed,p.ed)<0)return false;

最后我们得到总代码
可以在51Nod1264题提交试试

#include 
#include 
#include 
#include 
using namespace std;

struct point{
    double x,y;
};

struct vec{
    point st,ed;
}a,b;

double cj(point a,point b,point c){
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

bool jduge(vec p,vec q){
    if(min(p.st.x,p.ed.x)>max(q.st.x,q.ed.x))return false;
    if(min(p.st.y,p.ed.y)>max(q.st.y,q.ed.y))return false;
    if(min(q.st.x,q.ed.x)>max(p.st.x,p.ed.x))return false;
    if(min(q.st.y,q.ed.y)>max(p.st.y,p.ed.y))return false;

    if(cj(p.st,q.st,p.ed)*cj(p.st,p.ed,q.ed)<0)return false;
    if(cj(q.st,p.st,q.ed)*cj(q.st,q.ed,p.ed)<0)return false;

    return true;
}

int main(){
    int r;
    cin>>r;
    while(r--){
        cin>>a.st.x>>a.st.y>>a.ed.x>>a.ed.y>>b.st.x>>b.st.y>>b.ed.x>>b.ed.y;
        if(jduge(a,b))cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}