矢量&凸包学习笔记

矢量&凸包学习笔记

矢量

矢量（向量）的定义和表示法

定义：一条有方向的线段。

表示：如下图。

那么我们把这一条矢量写作：$AB$，它的长度为$a$，记作$\left|AB\right|$。

矢量的运算

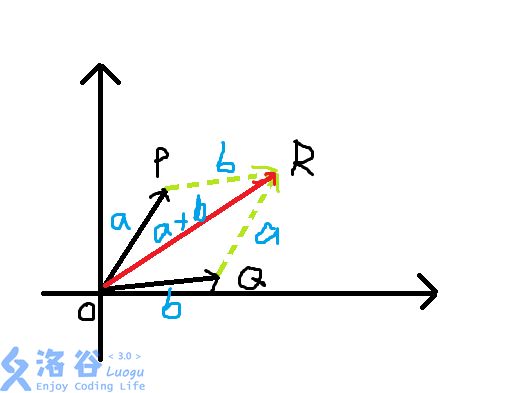
矢量的加减遵循三角形法则。

加：

根据三角形法则，$\left|AC\right|=\left|AB\right|+\left|BC\right|=a+b$ 。

减：

$\because \left|BC\right|=b$

$\therefore \left|CB\right|(\left|BC\right|)=-b$

$\therefore \left|B{C}^{\prime }\right|=-b$

$\therefore \left|A{C}^{\prime }\right|=\left|AB\right|+\left|B{C}^{\prime }\right|=a+(-b)=a-b$（三角形加法法则）

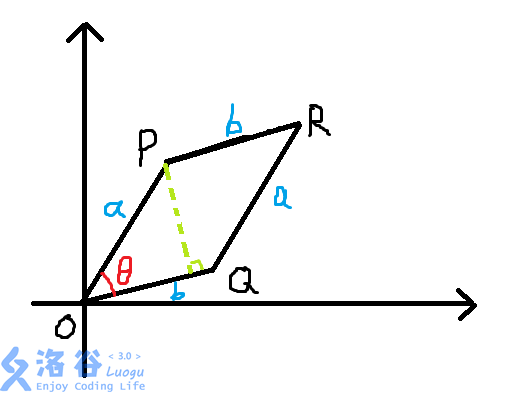
矢量的乘法遵循平行四边形法则。

如图，以矢量$OP$、$OQ$为邻边作平行四边形$OPRQ$。

根据三角形法则，可得$\left|OR\right|=a+b$。

我们不妨设$P$就为$OP$，$Q$就为$OQ$。

则定义$P\times Q$（$P$叉乘$Q$（不是点乘（$\bullet$）））为：

$$P\times Q=S_{OPRQ}=a\times b\times \sin (\theta )$$

当$O$为坐标原点时，也可以表示为：

$$P\times Q=\left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|=x_1{y}_2-x_2{y}_1$$

由此也可得$P\times Q=-(Q\times P)$。

同时可以通过$P\times Q$的值的正负求出$P$、$Q$的对应位置。

1. 当$P\times Q>0$时，$P$在$Q$的顺时针方向。
2. 当$P\times Q<0$时，$P$在$Q$的逆时针方向。
3. 当$P\times Q=0$时，$OP$与$OQ$共线。

凸包

1.模板

例题：P2742 【模板】二维凸包 / [USACO5.1]圈奶牛Fencing the Cows

题意：给一些点，求凸包周长。

做法：$Graham$：

先通过$sort$求出平面中最左下的点，然后以它为原点对其它点做极角排序，然后按极角从小到大依次插入一个$stack$中，每一次插入前看是否满足$stack$中的点和插入后的点是一个凸多边形：如是，就插入；否则一直$pop$直到满足条件为止。

最后$stack$中的点就是凸包的顶点。

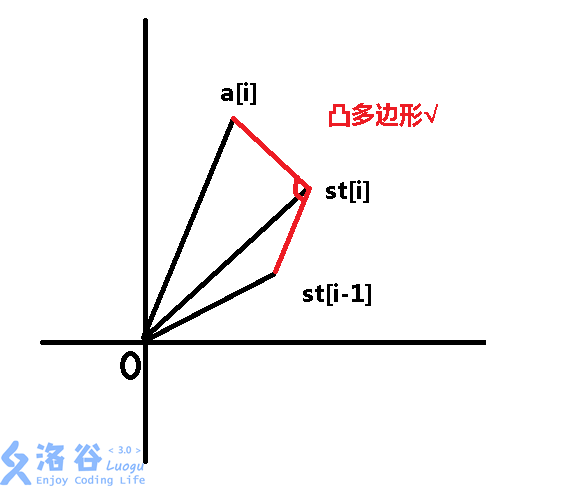
那么如何判断$stack$中的点和插入后的点是否是一个凸多边形呢：

当$cross(st[top-1],st[top],a[i])>0$时，根据右手法则，意味着由$st[i-1]$、$st[i]$、$a[i]$组成的图形是这样的：

而当$cross(st[top-1],st[top],a[i])<=0$时，那么根据右手法则，意味着由$st[i-1]$、$st[i]$、$a[i]$组成的图形是这样的：

代码如下：

#include

#define N 10010

using namespace std;

struct Point
{
    double x,y;
}a[N],st[N];

int n,top;
double ans;

double cross(Point a,Point b,Point c)//cross(a,b,c)为以a为原点的b、c的叉乘
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

double dis(Point a,Point b)//两点间距离
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

bool cmp(Point p,Point q)//极角排序（根据右手法则）
{
    double m=cross(a[1],p,q);
    if(m<0)return false;
    if(m>0)return true;
    return dis(a[1],p)<=dis(a[1],q);
}

int main()
{
    scanf("%d",&n);//点数
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&a[i].x,&a[i].y);
        if(i!=1&&a[i].y<a[1].y||(a[i].y==a[1].y&&a[i].x<a[1].x))swap(a[1],a[i]);//这样可以不用sort快速找到所有点中最左下角的点
    }
    sort(a+2,a+n+1,cmp);//除了最左下角的那个点a[1]，其它点以a[1]为原点进行极角排序
    st[++top]=a[1];//将a[1]入栈
    for(int i=2;i<=n;i++)
    {
        while(top>1&&cross(st[top-1],st[top],a[i])<=0)top--;//按上面说的判断是否为凸多边形
        st[++top]=a[i];
    }
    for(int i=2;i<=top;i++)ans+=dis(st[i-1],st[i]);
    ans+=dis(st[top],st[1]);
    printf("%.2lf\n",ans);
    return 0;
}

2.面积

例题：poj3348 cows

题意：给一些点，求凸包的面积除以$50$。

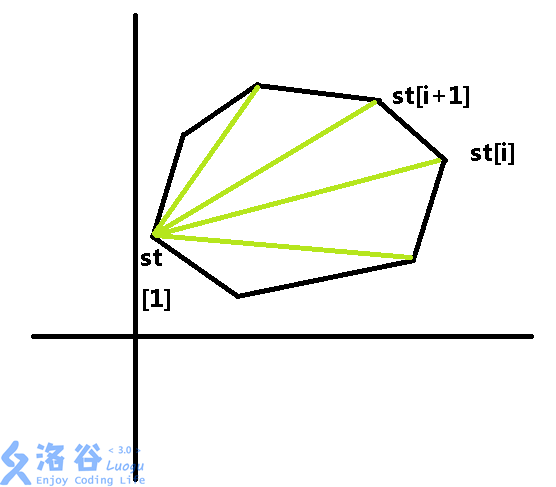
做法：我们可以先把一个凸包分割一下：

那么凸包面积就为所示所有三角形之和。

而每个三角形的面积即以三角形的两条绿线（在边界状态下，有1条绿线为黑线）为邻边的平行四边形的面积的一半。

即$cross(st[1],st[i],st[i+1])/2.0$。（平行四边形法则）

代码如下：

#include
#include
#include
#include
 
#define N 10010
 
using namespace std;
 
struct Point 
{
    int x,y;
}p[N],st[N];
 
int n,top;
double ans;
 
int cross(Point a,Point b,Point c)
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
 
double dis(Point a,Point b)
{
    return sqrt((double)((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)));
}
 
bool cmp(Point a,Point b)
{
    int m=cross(p[1],a,b);
    if(m>0)return true;
    if(m<0)return false;
    return dis(p[1],a)<dis(p[1],b);
}
 
void graham()//求凸包
{
    for(int i=2;i<=n;i++)
        if(p[i].y<p[1].y||(p[i].y==p[1].y&&p[i].x<p[1].x))swap(p[1],p[i]);
    sort(p+2,p+n+1,cmp);
    st[++top]=p[1],st[++top]=p[2];
    for(int i=3;i<=n;i++)
    {
        while(top>1&&cross(st[top-1],st[top],p[i])<=0)top--;
        st[++top]=p[i];
    }
}
 
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    graham();
    for(int i=1;i<top;i++)
        ans+=(double)cross(p[1],st[i],st[i+1])/2.0;//记得除以2
    printf("%d\n",(int)((double)ans/50.0));
    return 0;
}

3.隐秘的凸包

例题：P2116城墙/poj1113 Wall

题意：自己看题

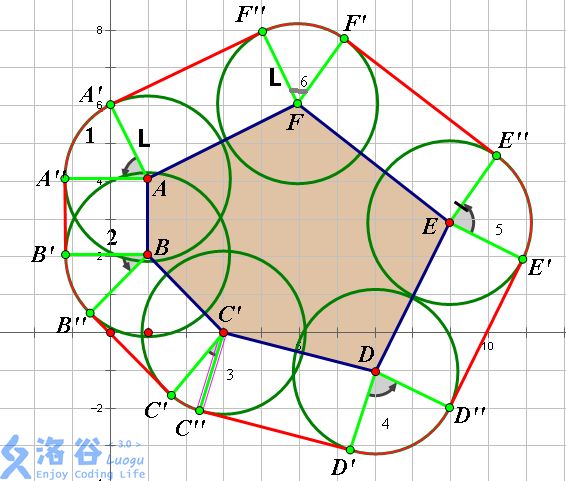
做法：我们自己画一下图，就可以发现最小长度总是凸包周长+一个半径为$L$的圆的周长。

具体证明：

以凸包为$6$边形为例：

如图，我们以每条边作长为边长，宽为$L$的矩形。

则红线部分就是所求答案。

对于$A^{\prime \prime }{B}^{\prime }+B^{\prime \prime }{C}^{\prime }+C^{\prime \prime }{D}^{\prime }+D^{\prime \prime }{E}^{\prime }+E^{\prime \prime }{F}^{\prime }+F^{\prime \prime }{A}^{\prime }$,我们可以知道它就是$AB+BC+CD+DE+EF+FA$，即凸包周长。

而对于剩下的几段圆弧，我们先经倒角后发现$\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6=360^o$。

那么$\stackrel{⌢}{A^{\prime }{A}^{\prime \prime }}+\stackrel{⌢}{B^{\prime }{B}^{\prime \prime }}+\stackrel{⌢}{C^{\prime }{C}^{\prime \prime }}+\stackrel{⌢}{D^{\prime }{D}^{\prime \prime }}+\stackrel{⌢}{E^{\prime }{E}^{\prime \prime }}+\stackrel{⌢}{F^{\prime }{F}^{\prime \prime }}=C=2\pi r=2\times acos(-1)\times L$

对于$n$边形凸包也是如此。

代码如下：

#include

#define N 10010

using namespace std;

struct Point
{
    double x,y;
}a[N],st[N];

int n,top;
double ans,l;

double cross(Point a,Point b,Point c)
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}

double dis(Point a,Point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

bool cmp(Point p,Point q)
{
    double m=cross(a[1],p,q);
    if(m<0)return false;
    if(m>0)return true;
    return dis(a[1],p)<=dis(a[1],q);
}

int main()
{
    scanf("%d%lf",&n,&l);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&a[i].x,&a[i].y);
        if(i!=1&&a[i].y<a[1].y)swap(a[1],a[i]);
    }
    sort(a+2,a+n+1,cmp);
    st[++top]=a[1];
    for(int i=2;i<=n;i++)
    {
        while(top>1&&cross(st[top-1],st[top],a[i])<=0)top--;
        st[++top]=a[i];
    }
    for(int i=2;i<=top;i++)ans+=dis(st[i-1],st[i]);
    ans+=dis(st[top],st[1]);
    //到此为止，已经把凸包的周长给算出来了。
    ans+=2*(acos(-1))*l;//再加上一个圆周长（C=2πr，acos(-1)=π）
    printf("%.0lf\n",ans);
    return 0;
}

4.练习

poj2007 Scrambled Polygon 模板，极角排序

P3829 [SHOI2012]信用卡凸包 总长=所有圆心的凸包周长+一个圆周长

poj1228 Grandpa’s Estate 稳定凸包。如果每边3点共线，说明凸包稳定，否则不稳定。

P1742 最小圆覆盖/P2533 [AHOI2012]信号塔 最小圆覆盖：随机增量法