FFT原理——详细推导理解FFT变换

概要：

FFT(Fast Fourier transform)：快速傅里叶变换，是DFT的工程化实现方法。
DFT直接求解太过于复杂，FFT方法根据DFT求解过程中旋转因子的性质并引入分治算法思想，大大简化计算过程，被广泛应用在频谱分析的工程实践中，如matlab，C，C++，CUDA等底层实现

一，DFT简介

频谱分析是信号处理中的重要环节，从傅里叶变换FT，到拉普拉斯变换LT，离散时间傅里叶变换DTFT，Z变换ZT，到我们所讲的离散傅里叶变换DFT（他们之间的联系和区别见我的其他博客）。
相比于其他变换，DFT被广泛应用的原因是其输入的时域信号是离散的，输出的频域结果也是离散的。这就极大方便了我们进行基于计算机的频谱计算，存储和分析，没办法数字信号处理是大趋势。
​ DFT变换的公式为：
$$X\left[k\right]=\sum _{n=0}^{N-1}x\left[n\right]e^{-jk\frac{2\pi }{K}n},k=0,1,2,...,K-1$$
这里不同于一般课本上的是，$k$的取值不再与输入信号$n$的长度$0\sim N-1$相同，而是自己设置。这是为了突出$k$的设置本质上是为了对以上 2pi 为周期的连续频谱离散化（DFT是DTFT连续频域结果离散化处理后的结果），也即频谱采样。

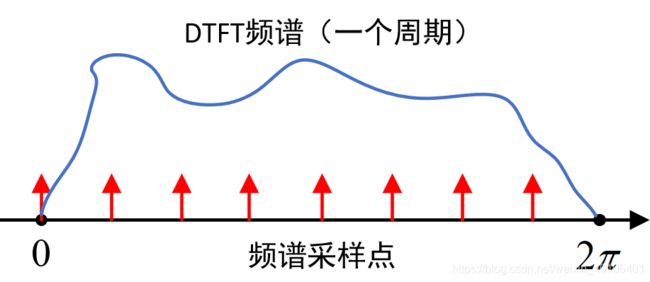
但为了分析方便，在FFT的计算过程中，我们依然使用$k=0\sim N-1$的选取策略。也即，如下：

$$X\left[k\right]=\sum _{n=0}^{N-1}x\left[n\right]e^{-jk\frac{2\pi }{N}n},k=0,1,2,...,N-1$$

上式直接求解当然可以，但是需要$N^2$次复数乘法和$N(N-1)$次复数加法：
$$X\left[k\right]=\sum _{n=0}^{N-1}x\left[n\right]e^{-jk\frac{2\pi }{N}n}\text{=}\sum _{n=0}^{N-1}x\left[n\right]W_N^{kn}$$
其中，$W$是需要替换的旋转因子：$W_N^{kn}=e^{-jk\frac{2\pi }{N}n},W=e^{-j\frac{2\pi }{N}}$

​ 使用FFT算法简化DFT计算过程就是依赖旋转因子$W$的一些性质，简化计算过程。

二、旋转因子$W$的性质

• 周期性：$W_N^{a+N}=W_N^a$
• 对称性：$W_N^{a+N/2}=-W_N^a$
• 缩放性：$W_N^2\text{=}{W}_{N/2}^1$

证明方法就是按旋转因子定义，直接拆开就行，就是代数变换。以上性质意味着值相同的就不用了再多计算一遍了，这就能简化DFT的计算过程。

三、FFT蝶形计算证明

​ FFT的计算过程运用了“分治算法”思想，并结合了旋转因子$W$的性质。具体证明过程如下：

1. 首先，我们把输入的时域信号$x[n],n=0,1,...,N-1$根据索引分为奇偶两部分：

$$f_{even}\left[n\right]=x\left[2n\right]$$

$$f_{odd}\left[n\right]=x\left[2n+1\right]$$

此时，索引范围为：$n=0,1,2,...,N/2-1$，

​ 2. 对DFT公式（3）进行化简：
$$X\left[k\right]=\sum _{n=0}^{N-1}x\left[n\right]W_N^{kn},k=0,1,...,N-1$$
得到：
$$X\left[k\right]=\sum _{n为偶数}x\left[n\right]W_N^{kn}+\sum _{n为奇数}x\left[n\right]W_N^{kn}k=0,1,...,N-1$$
这个过程很简单，如下图，就是按奇偶索引把求和分成两部分

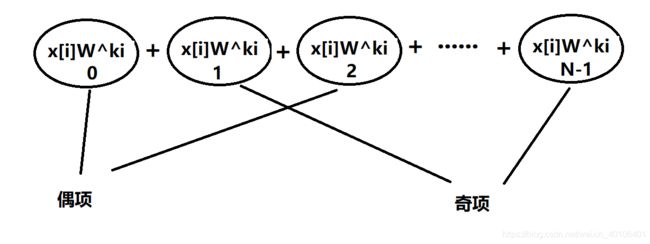
详细点写也即：
$$X\left[k\right]=\sum _{m=0}^{(N/2)-1}x\left[2m\right]W_N^{k\cdot 2m}+\sum _{m=0}^{(N/2)-1}x\left[2m+1\right]W_N^{k\cdot \left(2m+1\right)},k=0,1,...,N-1$$
根据旋转因子的缩放性，可以进一步换算：
$$X\left[k\right]=\sum _{m=0}^{(N/2)-1}{f}_{even}\left[m\right]W_{N/2}^{k\cdot m}+W_N^k\sum _{m=0}^{(N/2)-1}{f}_{odd}\left[m\right]W_{N/2}^{k\cdot m},k=0,1,...,N-1$$
也即：
$$X\left[k\right]=F_{even}\left[k\right]+W_N^k{F}_{odd}\left[k\right],k=0,1,...,N-1$$
其中，$F_{even}\left[k\right]$为偶数索引输入$f_{even}\left[n\right]$的DFT结果，$F_{odd}\left[k\right]$为奇数索引输入$f_{odd}\left[n\right]$的DFT结果。

3. 分析$F_{even}\left[k\right]$和$F_{odd}\left[k\right]$以便进一步转换：

   无论$F_{even}\left[k\right]$和$F_{odd}\left[k\right]$两个哪一个，他们的时域输入长度都为$(N/2)-1$，但此时的$ k=0,1,…,N-1$是输入信号长度的2倍。这就说明${{F}{even}}\left[ k \right]$和${{F}{odd}}\left[ k \right]$都是周期性的（可以理解为，N个点里包含了2个$2\pi $周期的频谱采样），也即:

$$F_{even}\left[k+N/2\right]=F_{even}\left[k\right]$$

$$F_{odd}\left[k+N/2\right]=F_{odd}\left[k\right]$$

4. 再次简化：

   根据式（13）可以知道，最终结果的前半部分，可以直接被得到：
   $$X\left[k\right]=F_{even}\left[k\right]+W_N^k{F}_{odd}\left[k\right],k=0,1,...,N/2-1$$
   又通过式（14,15），可以将（16）进一步转化：
   $$X\left[k+N/2\right]=F_{even}\left[k\right]+W_N^k{F}_{odd}\left[k\right],k=0,1,...,N/2-1$$
   通过，（16,17）可以看出：一个N点的DFT结果，可以被两个奇偶输入的DFT结果计算得到。举个例子也即，8点的DFT，可以被偶4点DFT结果和奇4点DFT结果计算得到，同理奇/偶4点DFT又可以被2点DFT结果计算得到，以此类推，分治求解。
   

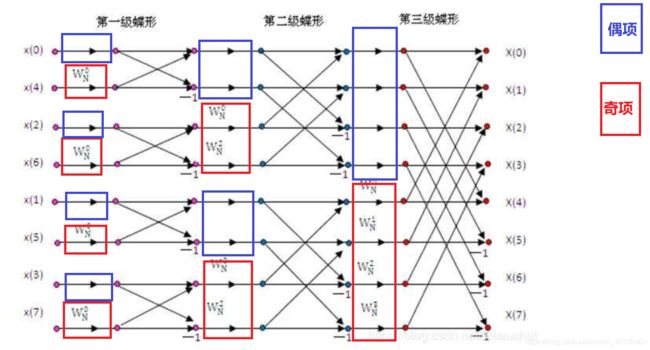
四、FFT计算过程

​ 步骤1：通过二进制镜像的方法，对时域信号的索引进行二进制编号，如下表最右列，从右向左反推输入计算序列，结果可以对应上图。

二进制：对应计算序列	转换	原始索引：对应二进制
000:0	←	0:000
100:4	←	1:001
010:2	←	2:010
110:6	←	3:011
001:1	←	4:100
101:5	←	5:101
011:3	←	6:110
111:7	←	7:11

​ 步骤2：奇偶项逐渐合并计算

五、其他说明

• 逆DFT过程也可以使用以上方法计算
• 以上方法为基2的方法，还有基4的方法，具体参考《数字信号处理——原理、算法与应用（第四版）》P380
• CSDN对Typora的md语法支持并不好，有些公式显示不出来，也没有标号，我已把PDF文档上传到了CSDN。