- 自动驾驶之心规划控制理论&实战课程
vsdvsvfhf
自动驾驶人工智能机器学习
单目3D与单目BEV全栈教程(视频答疑)多传感器标定全栈系统学习教程多传感器融合:毫米波雷达和视觉融合感知全栈教程(深度学习传统方式)多传感器融合跟踪全栈教程(视频答疑)多模态融合3D目标检测教程(视频答疑)规划控制理论&实战课程国内首个BEV感知全栈系列学习教程首个基于Transformer的分割检测视觉大模型视频课程CUDA与TensorRT部署实战课程(视频答疑)Occupancy从入门到精
- 【XR】优化SLAM SDK的稳定性
大江东去浪淘尽千古风流人物
xr
优化SLAMSDK的稳定性是确保增强现实(AR)和虚拟现实(VR)应用在各种环境和设备上都能稳定运行的关键。以下是一些主要的优化方法:1.传感器融合优化方法:将多个传感器的数据(如摄像头、加速度计、陀螺仪、磁力计)进行融合,以补偿单一传感器可能存在的误差。优势:提高了环境理解的准确性,减少了由于单一传感器误差导致的抖动和漂移现象。实例:ARKit和ARCore都利用了传感器融合技术来增强稳定性。2
- 无人机及固定机巢自动化控制软件技术详解
无人机技术圈
无人机技术无人机自动化运维
随着科技的飞速发展,无人机技术已成为众多行业中不可或缺的一部分,特别是在航拍、环境监测、农业植保、应急救援等领域展现出巨大潜力。无人机及固定机巢自动化控制软件作为支撑无人机高效、安全、自主运行的核心,集成了先进的系统架构、飞行控制算法、传感器技术、通信协议及数据处理能力。本文将从系统架构设计、飞行控制算法、传感器融合技术、通信与数据传输、自主巡航与定位、故障检测与预警、应急响应与处理、数据处理与报
- 华为问界M9:领跑未来智能交通的自动驾驶黑科技
华西建筑关联专业公司 华鲲智慧
华为自动驾驶科技
华为问界M9是一款高端电动汽车,其自动驾驶技术是该车型的重要卖点之一。华为在问界M9上采用了多种传感器和高级算法,实现了在不同场景下的自动驾驶功能,包括自动泊车、自适应巡航、车道保持、自动变道等。华为问界M9的自动驾驶技术惊艳之处在于其传感器融合和算法优化。通过多种传感器的融合,车辆可以更加精准地感知周围环境,并实现更加智能的决策和控制。同时,华为在自动驾驶算法方面也进行了大量的优化和改进,使得车
- 基于机器视觉的智能防疫巡检机器人结构设计
biyezuopinvip
机器人机器视觉防疫机器人巡检机器人毕业设计cad图纸论文
目录摘要11绪论31.1课题研究意义31.2智能防疫机器人的现状及发展31.3移动机器人技术的研究现状51.4智能防疫巡检机器人软件研究现状61.5多传感器融合研究现状61.6论文主要内容及结构安排72智能防疫巡检机器人系统需求分析与整体方案设计82.1系统设计的需求分析82.1.1功能需求82.1.2性能需求82.2智能防疫巡检机器人系统方案设计102.2.1整体方案102.2.2软件系统方案1
- veloview读二维雷达数据_Windows下VLP16激光雷达数据解析
大嘴博士
veloview读二维雷达数据
最近,实验室有一个对VLP16数据解析的需求,要求在Windows系统下单独把VLP16的数据解析整理出来,作为后期多传感器融合的一个必要基础准备。无奈从ROS转战Windows,网上查了查Windows系统下velodyne激光雷达的驱动,只找到了一个VeloView,很复杂,VeloView依赖winpcap、paraview、qt、python......单独摘出数据解析模块很麻烦。Kitw
- 环境配置:Udacity的Self-Driving项目安装运行
马上到我碗里来
#环境配置Udacity自动驾驶环境配置
前言Udacity的自动驾驶工程师纳米学位项目(Self-DrivingCarEngineerNanodegreeProgram)是一项面向学习者的前沿技术项目,旨在提供全面的自动驾驶工程师培训。该项目由Udacity与自动驾驶领域的领先公司和专业人士合作开发,涵盖了从传感器融合到深度学习等多个方面的内容。本篇内容将介绍此项目如何在自己的环境中进行配置。希望大家通过这个项目,能够在自动驾驶领域取得
- 基于Raspberry Pi的自动巡航与避障系统(二)
GT开发算法工程师
人工智能python矩阵opencv
在上一篇中,我们讨论了智能小车的避障逻辑实现,在本篇中,我们将进一步扩展智能小车的功能,包括更高级的避障策略、路径规划和导航功能,同时,我们还将提供相应的代码示例,以帮助读者更好地理解和实现这些功能。更高级的避障策略多传感器融合避障:结合使用超声波传感器、红外传感器和摄像头等多种传感器,通过数据融合算法,提高障碍物检测的准确性和可靠性。这样,智能小车可以更准确地判断障碍物的位置、大小和形状,从而采
- 【PMF代码复现及可视化】ICCV 2021 基于视觉感知的多传感器融合点云语义分割
努力弹琴的大风天
融合语义分割算法PMF人工智能计算机视觉
前言本文在Ubuntu18.04下,使用python3.6pytorch1.8.2+torchvision0.9.2环境运行。电脑配置:NVIDIAGeForceRTX3060。显卡不是特别好,运行训练代码花费4天11个小时。数据集非常大,原始数据集按照数据集格式和架构配置完成165.2GB左右,生成semantic-kitti-fov数据集28.1G。如果没有足够的空间,不建议跑这个论文项目。考
- 第一周文献阅读报告
半个轮子工
论文阅读物联网
文献阅读报告泛读1.《毫米波与太赫兹技术》2.《基于物联网的智能养老系统》3.《基于空间聚类的FMCW雷达双人行为识别方法》4.《太赫兹应用分析和展望》5.《车载毫米波雷达应用研究》6.《基于压力传感器的跌倒检测系统研究》7.《基于隐马尔可夫模型的老年人跌倒行为检测方法研究望》8.《矿用卡车毫米波雷达防碰撞系统的研究与应用》9.《基于YOLO网络的人体跌倒检测方法》10.《基于多传感器融合的老人跌
- 解锁多模态独特魅力-“机器人+Agent+多传感器融合+3DLLM”诠释终极组合大招!
xwz小王子
LLM机器人机器人3d自感知全能家务
01-Multiply算法背景01.01-触觉传感器触觉传感器是一种用于感知和测量物体接触力、形状、纹理和其他相关参数的传感器。它们模拟人类触觉系统,通过收集和解释物体与传感器之间的相互作用来获取信息。工作原理:触觉传感器使用不同的原理来感知接触力和其他触觉信息。常见的触觉传感器技术包括压电传感器、电容传感器、电阻传感器、光学传感器和弹性元件等。接触力测量:触觉传感器能够测量物体施加在其表面的接触
- 基于多传感器的后融合的目标跟踪如何实现?都有哪些基本流程?
自动驾驶之心
目标跟踪人工智能计算机视觉机器学习
点击下方卡片,关注“自动驾驶之心”公众号ADAS巨卷干货,即可获取讲师:Edison课程内容:基于多传感器后融合的目标跟踪(0.课前导学1.自动驾驶中的融合跟踪)笔记作者:王汝嘉0.课前导学0.1主讲人介绍0.2课程关键词0.3学习资料推荐1.自动驾驶中的融合跟踪1.1自动驾驶中的感知任务1.2多传感器融合的主要方法1.3多传感器融合跟踪的基本流程1.4多目标跟踪的数据集与性能指标以上内容均出自《
- 2020-05-20
bokli_dw
启发式算法:与过去的经验有关空缺几页少一张回顾遗传算法:交叉变异的概率每年考试是开卷做控制、天线、光通信。你的研究方向是什么?你觉得哪门智能信息处理方法可以在你的研究方向上很有帮助??第九章多传感器融合技术知识表示-模糊集-粗集神经网络-机器学习最重要的是搜索--智能算法:遗传、免疫、蚁群算法。每个算法在哪方面运用起来最得心应手就用哪个fusion--融合无人驾驶:融合很多的信息--信息融合是将来
- Ethzasl MSF编译与运行
稻壳特筑
SLAMC++多信息融合SLAM
多传感器融合框架EthzaslMSFFramework编译与运行:对应论文:ARobustandModularMulti-SensorFusionApproachAppliedtoMAVNavigation.2013RIOS.对应代码:https://github.com/ethz-asl/ethzasl_msf系统:Ubuntu16.03+ROSKinetic创建工作空间:mkdir-p/MSF
- 论文笔记(二十)VisuoTactile 6D Pose Estimation of an In-Hand Object using Vision and Tactile Sensor Data
墨绿色的摆渡人
文章深度学习物体姿势估计系统
VisuoTactile6DPoseEstimationofanIn-HandObjectusingVisionandTactileSensorData文章概括摘要1.介绍2.背景3.网络结构A.视觉触觉传感器融合B.姿势估计器C.损失函数4.数据集的生成A.触觉传感器不变的姿态估计B.数据收集设置C.数据集特征5.实验A.网络训练设置B.硬件部署6.结果A.量化评估B.定性评价C.消融研究D.与
- 多传感器融合SLAM数学学习历程
SensorFusion
多传感器融合学习
多传感器融合SLAM数学学习历程>>>流形和流形空间(姿态)https://blog.csdn.net/professor_Xie/article/details/131911894fast-lio带着问题看知识欧式空间和流形空间的区别和联系?基本结构:欧式空间是我们熟悉的传统三维空间,其中的点由三个实数(x、y、z)表示,具有直角坐标系。在欧式空间中,可以进行常规的线性运算和加法操作。而流形空间
- 革命性突破!全新多传感器辅助惯性导航系统,效能与精准度并肩
3DCV
自动驾驶人工智能机器学习计算机视觉深度学习
作者:小柠檬|来源:3DCV在公众号「3DCV」后台,回复「原论文」获取论文和项目地址大家好,给大家推荐一种高效、强大的多传感器辅助惯性导航系统,具有在线校准功能,能够融合IMU、摄像头、LiDAR、GPS/GNSS和车轮传感器。使用案例:VINS/VIO、GPS-INS、LINS/LIO、用于定位和建图的多传感器融合(SLAM)。原文链接:革命性突破!全新多传感器辅助惯性导航系统,效能与精准度并
- AI加速器与机器学习算法:协同设计与进化
江太翁
人工智能人工智能机器学习算法
作者|ShashankPrasanna翻译|胡燕君此刻,你应该是在电脑或手机上看这篇文章。不管怎样,这些机器都属于现代计算机,它们都有中央处理器(CPU)和其他为特定功能服务的专用芯片,例如显卡、声卡、网卡、传感器融合等。处理特定任务时,专用处理器往往比通用CPU更快更高效。计算机发展早期,CPU都会和专用处理器配合使用。1970年代的8位和16位CPU需要依赖软件来模拟浮点指令,因此执行浮点运算
- 点云从入门到精通技术详解100篇-基于多传感器融合的紧耦合 SLAM 算法
格图素书
自动驾驶人工智能机器学习
目录前言多传感器融合的SLAM相关设备及技术介绍2.1三维刚体运动模型2.1.1坐标系变换
- Autoware 开源框架车辆运动学建模推导
秃头队长
Autoware
学习Autoware开源框架的资料整理,侵删!开源自动驾驶框架Autoware介绍Autoware包含以下模块:1.定位:通过结合GNSS和IMU传感器的3D地图和SLAM算法来实现定位2.检测:使用具有传感器融合算法和深度神经网络的摄像机以及LiDAR3.预测和规划:基于概率机器人技术和基于规则的系统,部分还使用深度神经网络4.控制:Autoware向车辆输出的速度和角速度的扭曲量以上四个模块覆
- 自动驾驶感知-预测-决策-规划-控制学习(3):感知方向文献阅读笔记
棉花糖永远滴神
自动驾驶学习笔记
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、文章主题二、摘要阅读1.名词理解①点云是什么?②二维图像分割器③轻量化卷积网络提取特征④单模态表达和多模态特征融合的区别⑤基于ROS的多传感器融合感知⑥TensorRT工具2.总结摘要三、绪论解析1.首先分析了车道线检测方面有三类工作2.又分析了三维目标检测研究的三类工作3.综述各章节内容四、硬件与软件设计1.总体方案
- 高精地图新基线 | SuperFusion:多层次Lidar-Camera融合,nuScenes SOTA!
自动驾驶之心
点击下方卡片,关注“自动驾驶之心”公众号ADAS巨卷干货,即可获取点击进入→自动驾驶之心【多传感器融合】技术交流群后台回复【SuperFusion】获取本文代码!!!摘要环境的高精(HD)语义地图生成是自动驾驶的一个重要组成部分。现有方法通过融合不同的传感器模式(如激光雷达和相机),在这项任务中取得了良好的性能。然而,目前的工作基于原始数据或网络特征级融合,仅考虑短距离高精地图生成,限制了其部署到
- 多传感器融合学习笔记
AI视觉网奇
3D视觉学习笔记
目录BevFusionBEVFormer(ECCV2022)eagerMOT利用2D+3D数据多目标跟踪Download3Dand2Ddetections,whichonestodownloaddependsonwhatyouwanttorun:BevFusion最小的模型530多mBevFusion是一种多传感器融合技术,它可以将来自不同传感器(如LiDAR和相机)的数据融合到一个统一的BEV表
- 车载毫米波雷达及芯片新趋势研究3--自动驾驶、国产替代与外延场景需求快速增长打开市场空间
奔袭的算法工程师
行业资讯自动驾驶人工智能机器学习目标检测深度学习
3.1多传感器融合路线优势将不断扩大,引发更多毫米波雷达及芯片需求纯视觉自动驾驶路线是通过以光学摄像头为传感器结合大量算法训练以模拟人类视觉驾驶为逻辑的自动驾驶方案。纯视觉方案“轻硬件、重软件”,由其采用的摄像头成本较低,纯视觉方案的整体硬件成本较低。多传感器融合自动驾驶路线的原理是通过多种类型传感器共同收集路况信息和数据,并通过算法自动分析和综合完成自动驾驶决策的方案。多传感器融合路线能够集
- 【多传感器融合导航论文阅读】
今天我刷leetcode了吗
论文阅读学习方法
多传感器融合导航论文积累知识点总结因子图一致因子图文献阅读笔记[IF18.6]知识点总结因子图FactorGraph是概率图的一种,是对函数因子分解的表示图,一般内含两种节点,变量节点和函数节点。因子图存在着:两类节点:变量节点和对应的函数节点变量节点所代表的变量是函数节点的自变量。同类节点之间没有边直接相连。一致因子图一致性指的是在该框架中能够保持一致性地更新变量的值,使得整个概率图模型中的变量
- 【论文笔记】Learned Fusion: 3D Object Detection using Calibration-Free Transformer Feature Fusion
byzy
#激光雷达与图像融合论文阅读目标检测计算机视觉自动驾驶深度学习
原文链接:https://arxiv.org/abs/2312.090821.引言目前的3D目标检测一来传感器的校准信息。这种情况下,校准信息需要及其精确,但在产品尺度上,获取高质量校准信息是很困难的(需要逐传感器校准,且运行过程中可能会变化)。本文基于Transformer,提出无需校准信息的传感器融合方法。3.方法从基于Transformer的方法中直接移除校准信息会导致训练困难。3.1Tra
- UBX M8T-10 DSP开发和NMEA解析
汪汪星河
算法
特殊名词:l惯性导航(DR)解决方案采用惯性传感器(陀螺仪和加速计)来辅助GNSS定位技术。l无约束惯性导航(UDR)解决方案持续测量与监测车辆加速度及其方向变化,再通过传感器融合技术将测量数据与GNSS数据进行整合,实时计算并优化分析出更精准的位置结果。l车载惯性导航(ADR)解决方案在此基础上则更进一步,可将车辆轮速脉冲传感器的数据进行整合,实现更高精度的位置计算结果。UbxM8:Ublox-
- 《LIO-SAM阅读笔记》1.IMU预积分模块
Jiqiang_z
机器人linux笔记
前言:LIO-SAM是一个多传感器融合的紧耦合SLAM框架,融合的传感器类型有雷达、IMU和GPS,其中雷达和IMU在LIO-SAM框架中必须使用的。LIO-SAM的优化策略采用了GTSAM库,GTSAM库采用了因子图的优化方法,其提供了一些列C++的外部接口,以便用户方便传入参数等进行优化。特别的是GTSAM库专门单独设计关于IMU计算与优化的接口。IMU预积分模块在LIO-SAM源码中写在了i
- 当我们在讨论多模态融合时?我们究竟在讨论什么?最新多源融合综述!
自动驾驶之心
点击下方卡片,关注“自动驾驶之心”公众号ADAS巨卷干货,即可获取今天自动驾驶之心很荣幸邀请到Xizhu来分享自动驾驶最新的多源传感器融合综述!如果您有相关工作需要分享,请在文末联系我们!>>点击进入→自动驾驶之心【多传感器融合】技术交流群论文作者|Xizhu编辑|自动驾驶之心很荣幸来分享我们的多源数据融合综述~这篇综述文章所关注的核心问题是自动驾驶系统中的多源数据融合技术。多源数据融合对自动驾驶
- 机器人制作开源方案 | “校园卫士”-智能巡检机器人
Robotway
机器人开源
作者:程训聪、柳贺凯、赵坤峰、叶智超、高仁伟单位:黑龙江科技大学指导老师:邵文冕、李杨1.摘要针对校园巡检需求设计机器人本体结构,借助Arduino作为控制核心的巡检机器人控制系统构建方法研究了巡检机器人在校园环境下的导航、控制、多传感器融合等问题。结果表明:该套系统的研发有效解决了校园巡检机器人的攀爬障碍、火灾检测、智能人脸检测、佩戴口罩识别等问题,通过采用分布式结构,保障了整个系统的实时性,实
- Enum用法
不懂事的小屁孩
enum
以前的时候知道enum,但是真心不怎么用,在实际开发中,经常会用到以下代码:
protected final static String XJ = "XJ";
protected final static String YHK = "YHK";
protected final static String PQ = "PQ";
- 【Spark九十七】RDD API之aggregateByKey
bit1129
spark
1. aggregateByKey的运行机制
/**
* Aggregate the values of each key, using given combine functions and a neutral "zero value".
* This function can return a different result type
- hive创建表是报错: Specified key was too long; max key length is 767 bytes
daizj
hive
今天在hive客户端创建表时报错,具体操作如下
hive> create table test2(id string);
FAILED: Execution Error, return code 1 from org.apache.hadoop.hive.ql.exec.DDLTask. MetaException(message:javax.jdo.JDODataSto
- Map 与 JavaBean之间的转换
周凡杨
java自省转换反射
最近项目里需要一个工具类,它的功能是传入一个Map后可以返回一个JavaBean对象。很喜欢写这样的Java服务,首先我想到的是要通过Java 的反射去实现匿名类的方法调用,这样才可以把Map里的值set 到JavaBean里。其实这里用Java的自省会更方便,下面两个方法就是一个通过反射,一个通过自省来实现本功能。
1:JavaBean类
1 &nb
- java连接ftp下载
g21121
java
有的时候需要用到java连接ftp服务器下载,上传一些操作,下面写了一个小例子。
/** ftp服务器地址 */
private String ftpHost;
/** ftp服务器用户名 */
private String ftpName;
/** ftp服务器密码 */
private String ftpPass;
/** ftp根目录 */
private String f
- web报表工具FineReport使用中遇到的常见报错及解决办法(二)
老A不折腾
finereportweb报表java报表总结
抛砖引玉,希望大家能把自己整理的问题及解决方法晾出来,Mark一下,利人利己。
出现问题先搜一下文档上有没有,再看看度娘有没有,再看看论坛有没有。有报错要看日志。下面简单罗列下常见的问题,大多文档上都有提到的。
1、没有返回数据集:
在存储过程中的操作语句之前加上set nocount on 或者在数据集exec调用存储过程的前面加上这句。当S
- linux 系统cpu 内存等信息查看
墙头上一根草
cpu内存liunx
1 查看CPU
1.1 查看CPU个数
# cat /proc/cpuinfo | grep "physical id" | uniq | wc -l
2
**uniq命令:删除重复行;wc –l命令:统计行数**
1.2 查看CPU核数
# cat /proc/cpuinfo | grep "cpu cores" | u
- Spring中的AOP
aijuans
springAOP
Spring中的AOP
Written by Tony Jiang @ 2012-1-18 (转)何为AOP
AOP,面向切面编程。
在不改动代码的前提下,灵活的在现有代码的执行顺序前后,添加进新规机能。
来一个简单的Sample:
目标类:
[java]
view plain
copy
print
?
package&nb
- placeholder(HTML 5) IE 兼容插件
alxw4616
JavaScriptjquery jQuery插件
placeholder 这个属性被越来越频繁的使用.
但为做HTML 5 特性IE没能实现这东西.
以下的jQuery插件就是用来在IE上实现该属性的.
/**
* [placeholder(HTML 5) IE 实现.IE9以下通过测试.]
* v 1.0 by oTwo 2014年7月31日 11:45:29
*/
$.fn.placeholder = function
- Object类,值域,泛型等总结(适合有基础的人看)
百合不是茶
泛型的继承和通配符变量的值域Object类转换
java的作用域在编程的时候经常会遇到,而我经常会搞不清楚这个
问题,所以在家的这几天回忆一下过去不知道的每个小知识点
变量的值域;
package 基础;
/**
* 作用域的范围
*
* @author Administrator
*
*/
public class zuoyongyu {
public static vo
- JDK1.5 Condition接口
bijian1013
javathreadConditionjava多线程
Condition 将 Object 监视器方法(wait、notify和 notifyAll)分解成截然不同的对象,以便通过将这些对象与任意 Lock 实现组合使用,为每个对象提供多个等待 set (wait-set)。其中,Lock 替代了 synchronized 方法和语句的使用,Condition 替代了 Object 监视器方法的使用。
条件(也称为条件队列或条件变量)为线程提供了一
- 开源中国OSC源创会记录
bijian1013
hadoopsparkMemSQL
一.Strata+Hadoop World(SHW)大会
是全世界最大的大数据大会之一。SHW大会为各种技术提供了深度交流的机会,还会看到最领先的大数据技术、最广泛的应用场景、最有趣的用例教学以及最全面的大数据行业和趋势探讨。
二.Hadoop
&nbs
- 【Java范型七】范型消除
bit1129
java
范型是Java1.5引入的语言特性,它是编译时的一个语法现象,也就是说,对于一个类,不管是范型类还是非范型类,编译得到的字节码是一样的,差别仅在于通过范型这种语法来进行编译时的类型检查,在运行时是没有范型或者类型参数这个说法的。
范型跟反射刚好相反,反射是一种运行时行为,所以编译时不能访问的变量或者方法(比如private),在运行时通过反射是可以访问的,也就是说,可见性也是一种编译时的行为,在
- 【Spark九十四】spark-sql工具的使用
bit1129
spark
spark-sql是Spark bin目录下的一个可执行脚本,它的目的是通过这个脚本执行Hive的命令,即原来通过
hive>输入的指令可以通过spark-sql>输入的指令来完成。
spark-sql可以使用内置的Hive metadata-store,也可以使用已经独立安装的Hive的metadata store
关于Hive build into Spark
- js做的各种倒计时
ronin47
js 倒计时
第一种:精确到秒的javascript倒计时代码
HTML代码:
<form name="form1">
<div align="center" align="middle"
- java-37.有n 个长为m+1 的字符串,如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配,则两个字符串可以联接
bylijinnan
java
public class MaxCatenate {
/*
* Q.37 有n 个长为m+1 的字符串,如果某个字符串的最后m 个字符与某个字符串的前m 个字符匹配,则两个字符串可以联接,
* 问这n 个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
*/
public static void main(String[] args){
- mongoDB安装
开窍的石头
mongodb安装 基本操作
mongoDB的安装
1:mongoDB下载 https://www.mongodb.org/downloads
2:下载mongoDB下载后解压
- [开源项目]引擎的关键意义
comsci
开源项目
一个系统,最核心的东西就是引擎。。。。。
而要设计和制造出引擎,最关键的是要坚持。。。。。。
现在最先进的引擎技术,也是从莱特兄弟那里出现的,但是中间一直没有断过研发的
- 软件度量的一些方法
cuiyadll
方法
软件度量的一些方法http://cuiyingfeng.blog.51cto.com/43841/6775/在前面我们已介绍了组成软件度量的几个方面。在这里我们将先给出关于这几个方面的一个纲要介绍。在后面我们还会作进一步具体的阐述。当我们不从高层次的概念级来看软件度量及其目标的时候,我们很容易把这些活动看成是不同而且毫不相干的。我们现在希望表明他们是怎样恰如其分地嵌入我们的框架的。也就是我们度量的
- XSD中的targetNameSpace解释
darrenzhu
xmlnamespacexsdtargetnamespace
参考链接:
http://blog.csdn.net/colin1014/article/details/357694
xsd文件中定义了一个targetNameSpace后,其内部定义的元素,属性,类型等都属于该targetNameSpace,其自身或外部xsd文件使用这些元素,属性等都必须从定义的targetNameSpace中找:
例如:以下xsd文件,就出现了该错误,即便是在一
- 什么是RAID0、RAID1、RAID0+1、RAID5,等磁盘阵列模式?
dcj3sjt126com
raid
RAID 1又称为Mirror或Mirroring,它的宗旨是最大限度的保证用户数据的可用性和可修复性。 RAID 1的操作方式是把用户写入硬盘的数据百分之百地自动复制到另外一个硬盘上。由于对存储的数据进行百分之百的备份,在所有RAID级别中,RAID 1提供最高的数据安全保障。同样,由于数据的百分之百备份,备份数据占了总存储空间的一半,因而,Mirror的磁盘空间利用率低,存储成本高。
Mir
- yii2 restful web服务快速入门
dcj3sjt126com
PHPyii2
快速入门
Yii 提供了一整套用来简化实现 RESTful 风格的 Web Service 服务的 API。 特别是,Yii 支持以下关于 RESTful 风格的 API:
支持 Active Record 类的通用API的快速原型
涉及的响应格式(在默认情况下支持 JSON 和 XML)
支持可选输出字段的定制对象序列化
适当的格式的数据采集和验证错误
- MongoDB查询(3)——内嵌文档查询(七)
eksliang
MongoDB查询内嵌文档MongoDB查询内嵌数组
MongoDB查询内嵌文档
转载请出自出处:http://eksliang.iteye.com/blog/2177301 一、概述
有两种方法可以查询内嵌文档:查询整个文档;针对键值对进行查询。这两种方式是不同的,下面我通过例子进行分别说明。
二、查询整个文档
例如:有如下文档
db.emp.insert({
&qu
- android4.4从系统图库无法加载图片的问题
gundumw100
android
典型的使用场景就是要设置一个头像,头像需要从系统图库或者拍照获得,在android4.4之前,我用的代码没问题,但是今天使用android4.4的时候突然发现不灵了。baidu了一圈,终于解决了。
下面是解决方案:
private String[] items = new String[] { "图库","拍照" };
/* 头像名称 */
- 网页特效大全 jQuery等
ini
JavaScriptjquerycsshtml5ini
HTML5和CSS3知识和特效
asp.net ajax jquery实例
分享一个下雪的特效
jQuery倾斜的动画导航菜单
选美大赛示例 你会选谁
jQuery实现HTML5时钟
功能强大的滚动播放插件JQ-Slide
万圣节快乐!!!
向上弹出菜单jQuery插件
htm5视差动画
jquery将列表倒转顺序
推荐一个jQuery分页插件
jquery animate
- swift objc_setAssociatedObject block(version1.2 xcode6.4)
啸笑天
version
import UIKit
class LSObjectWrapper: NSObject {
let value: ((barButton: UIButton?) -> Void)?
init(value: (barButton: UIButton?) -> Void) {
self.value = value
- Aegis 默认的 Xfire 绑定方式,将 XML 映射为 POJO
MagicMa_007
javaPOJOxmlAegisxfire
Aegis 是一个默认的 Xfire 绑定方式,它将 XML 映射为 POJO, 支持代码先行的开发.你开发服 务类与 POJO,它为你生成 XML schema/wsdl
XML 和 注解映射概览
默认情况下,你的 POJO 类被是基于他们的名字与命名空间被序列化。如果
- js get max value in (json) Array
qiaolevip
每天进步一点点学习永无止境max纵观千象
// Max value in Array
var arr = [1,2,3,5,3,2];Math.max.apply(null, arr); // 5
// Max value in Jaon Array
var arr = [{"x":"8/11/2009","y":0.026572007},{"x"
- XMLhttpRequest 请求 XML,JSON ,POJO 数据
Luob.
POJOjsonAjaxxmlXMLhttpREquest
在使用XMlhttpRequest对象发送请求和响应之前,必须首先使用javaScript对象创建一个XMLHttpRquest对象。
var xmlhttp;
function getXMLHttpRequest(){
if(window.ActiveXObject){
xmlhttp:new ActiveXObject("Microsoft.XMLHTTP
- jquery
wuai
jquery
以下防止文档在完全加载之前运行Jquery代码,否则会出现试图隐藏一个不存在的元素、获得未完全加载的图像的大小 等等
$(document).ready(function(){
jquery代码;
});
<script type="text/javascript" src="c:/scripts/jquery-1.4.2.min.js&quo

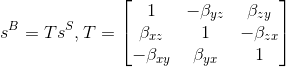

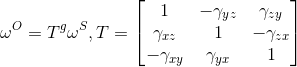
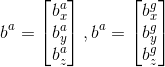
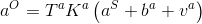

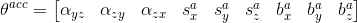

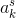
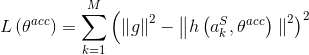
 ,将一系列角速度参数和由加速度标定得到的初始重力范
,将一系列角速度参数和由加速度标定得到的初始重力范 数(例如重力方向的单位矢量),最终返回一个重力范数
数(例如重力方向的单位矢量),最终返回一个重力范数 ,使用角速度测量在k-1到k之间的静态时间间隔得到。
,使用角速度测量在k-1到k之间的静态时间间隔得到。 可以是通过积分输入角速度计算最终方向的任何积分算法。校准陀螺仪需要估计的未知参数向量是:
可以是通过积分输入角速度计算最终方向的任何积分算法。校准陀螺仪需要估计的未知参数向量是:

 是在第k个时间窗口中测得的加速度静态间隔中校准的加速计读数。
是在第k个时间窗口中测得的加速度静态间隔中校准的加速计读数。 是对k-1到k时间间隔中的角速度积分。
是对k-1到k时间间隔中的角速度积分。 是最小化上面两个值差LM算法得到的角速度校准参数
是最小化上面两个值差LM算法得到的角速度校准参数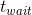 (见图1),对于每个t时刻的加速度采样
(见图1),对于每个t时刻的加速度采样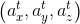 ,我们计算方差大小
,我们计算方差大小![\zeta \left ( t \right )=\sqrt{[var_{t_{w}}(a_{x}^{t})]^{2}+[var_{t_{w}}(a_{y}^{t})]^{2}+[var_{t_{w}}(a_{z}^{t})]^{2}}](http://img.e-com-net.com/image/info8/c1f3101f9cf841df84619001df7123dd.gif)
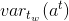 是计算加速度在时间间隔
是计算加速度在时间间隔 的加速度方差
的加速度方差 内的方差
内的方差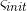
 中使用Allan方差校准方法中的时间间隔
中使用Allan方差校准方法中的时间间隔 为2s
为2s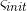 的六倍
的六倍
 将所考虑的三维角速度转换为真实的斜对称矩阵表示的四元数变换运算符
将所考虑的三维角速度转换为真实的斜对称矩阵表示的四元数变换运算符
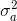 定义如下
定义如下

 是第k个时间间隔的t秒平均值,k是总考虑时间分段的间隔数
是第k个时间间隔的t秒平均值,k是总考虑时间分段的间隔数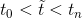 ,其中
,其中
 ,如图一所示
,如图一所示 值为50秒(参见图4)。
值为50秒(参见图4)。
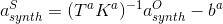

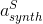 和
和 分别是非正交传感器帧和相关正交帧中的合成加速度。
分别是非正交传感器帧和相关正交帧中的合成加速度。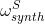 和
和 分别是非正交传感器帧和相关正交帧中的合成角速度。式23和式24来自式6和式7中提出的模型。我们用来评估结果质量的指标是:
分别是非正交传感器帧和相关正交帧中的合成角速度。式23和式24来自式6和式7中提出的模型。我们用来评估结果质量的指标是: 。给定
。给定 ,我们可以在BF中表示我们的校准矢量。
,我们可以在BF中表示我们的校准矢量。 可从偏差矩阵中包含的数据(见公式1的讨论)并遵循[14][5]中提出的简单方法轻松估计。
可从偏差矩阵中包含的数据(见公式1的讨论)并遵循[14][5]中提出的简单方法轻松估计。