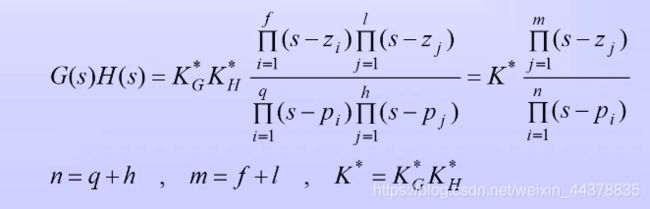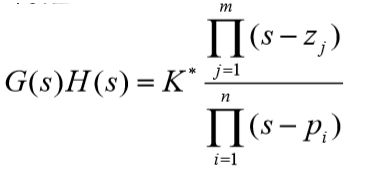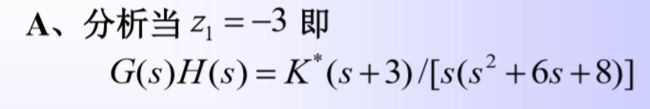(十四)【自控原理】(第四章 根轨迹法)
文章目录
- A 根轨迹法的基本概念
- B 闭环零极点与开环零极点的关系
- C 根轨迹方程
- C 绘制根轨迹的法则
- C.a 根轨迹法则介绍
- C.b 根轨迹法则(常规根轨迹)
- D 广义根轨迹
- D.a 参数根轨迹
- D.a.a 开环零点变化时的根轨迹
- D.a.b 开环极点变化时的根轨迹
- D.b 附加开环零点的作用
- E 系统性能的分析
引言
闭环控制系统的稳定性和性能指标主要由闭环系统的极点在复数平面上的位置决定。
分析和设计系统时确定闭环极点(即特征根)在复平 面的位置是十分有意义的:
- 闭环系统的极点在复平面的位置决定了系统的稳 定性
- 系统的性能指标也主要由闭环极点的位置决定
通过求解高阶代数方程确定闭环极点是困难的;
闭环系统的极点与系统的参数有关,如开环增益等;
希望找到一种不用求解代数方程,就能确定当某个参 数变化时极点的位置的方法:
1948年伊文思(Walter R.Evans)提出了根轨迹法; 根轨迹方法能够确定当某个参数变化时,闭环极点在 复数平面上移动的轨迹。
A 根轨迹法的基本概念
什么是根轨迹

K从0变成0.5时,一个极点从0沿着实轴移动到-1点,另一个极点从-2沿着实轴移动到-1点。
K从0.5变为1时,极点一个向上移动1,另一个向下移动1。当K变为无穷大时,极点分别向上下移动到无穷。图中的红线就是这个系统的根轨迹。
根轨迹定义:根轨迹是指当系统开环的某个参 数(如开环增益)从零变化到无 穷大时,闭环特征方程的根在复 平面上移动的轨迹。
根据所绘制的根轨迹图可知该系统:
(1)稳定性:当开环增益从零变到无 穷时,上面图中的根轨迹不会 越过虚轴进入右半s平面,因 此对所有的K值都是稳定的。
(2)动态性能
K>0时,两个极点始终位于平面的左半平面,系统稳定;
0
K>0.5时,两个极点是共轭复根,处于欠阻尼状态, 阶跃响应为振荡衰减过程。且超调量将随着K值增大而增大。
(3)稳态性能
开环系统在坐标原 点有一个极点,所以系 统属I型系统,因而根 轨迹上的K值就是静态 速度误差系数。如果给 定系统的稳态误差要求, 则由根轨迹图可以确定 闭环极点位置的容许范 围。
B 闭环零极点与开环零极点的关系
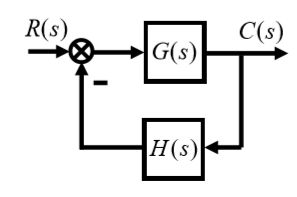
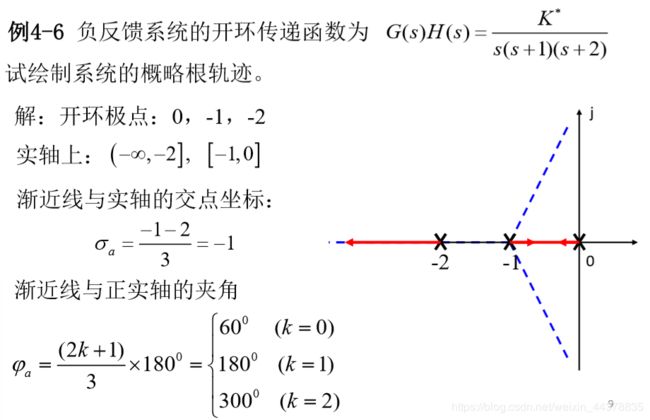
1、典型控制系统
闭环系统的特征方程: 1 + G ( s ) H ( s ) = 0 1+G(s)H(s)=0 1+G(s)H(s)=0
2前向通路传递函数
在一般情况下,前向通路传递函数可表示为:

因式分解为首1形式
3 反馈通路传递函数
在一般情况下,反馈通路传递函数可表示为:

5 闭环传递函数
将前向通路传递函数G(s)和反馈通路传递函数 H(s)代入
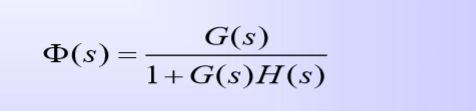
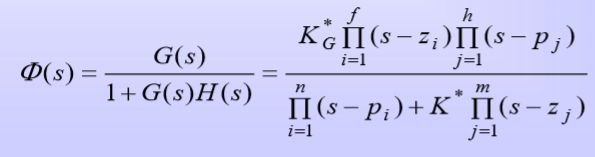
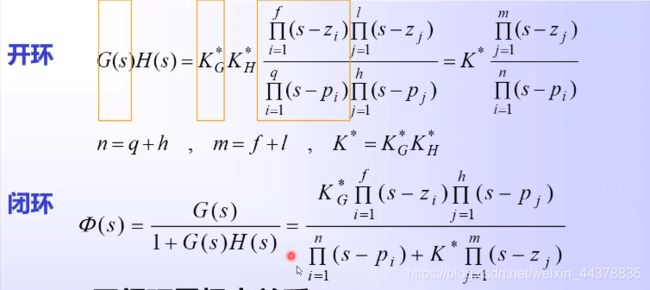
6 开闭环零极点关系
(1)闭环系统根轨迹增益=开环系统前向通路根轨迹增益 K G ∗ K_G^* KG∗。
对单位反馈( K H ∗ = 1 K_H^*=1 KH∗=1),闭环系统根轨迹增益=开环系统根轨迹益( K ∗ = K G ∗ K^* =K_G^* K∗=KG∗)。
(2)闭环零点由开环前向通路传递函数的零点和反馈通路传递数的极点所组成。对单位反馈统,闭环零点=开环零点。
(3)闭环极点与开环零点、开环极点以及根轨迹增益 K ∗ K^* K∗均有关(分母)
C 根轨迹方程
开环传递函数
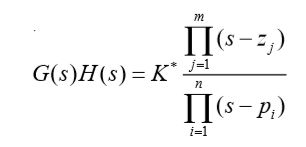
其中, z j 、 p i z_j、p_i zj、pi分别为开环零、极点。
0 ≤ K ∗ ≤ ∞ 0\le K^*\le \infty 0≤K∗≤∞为开环根轨迹增益,并假设 n ≥ m n\ge m n≥m
闭环系统特征方程: 1 + G ( s ) H ( s ) = 0 1+G(s)H(s)=0 1+G(s)H(s)=0
由于闭环极点就是特征方程的根,该方程又称为根轨迹方程。
1 系统闭环特征方程
由闭环传函可得到系统闭环特征方程为:

通常写成: G ( s ) H ( s ) = − 1 G(s)H(s)=-1 G(s)H(s)=−1
2 根轨迹方程
当系统有m个开环零点和n个开环极点时:
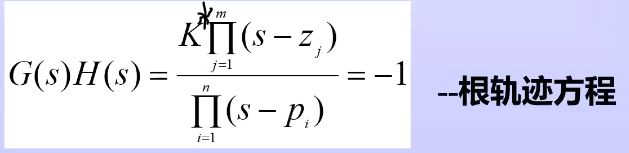
− 1 = e j ( 2 k + 1 ) π , k = 0 , ± 1... -1=e^{j(2k+1)\pi},k=0,\pm1... −1=ej(2k+1)π,k=0,±1...
- 由于 0 ≤ K ∗ ≤ ∞ 0\le K^*\le \infty 0≤K∗≤∞ ,所以任何复数s均满足模值方程;
相角方程是确定复数s是否为根轨迹上的点的充分必要条件;- 利用模值方程可确定根轨迹上某个点对应的K*值。
如何利用相方程确定某一个点是否属于根轨迹的点以及所对应的根轨迹增益的值:

s1代入得到 − π -\pi −πs2代入得到 π \pi π都满足相方程,故s1、s2这两点都是根轨迹上的点。
再有模值方程求出对应的根轨迹增益。
上述的方法是使用试错的方法验证某个点是否在根轨迹上。如果要求出K在连续变化时所有根轨迹上的点是比较麻烦的。因此需要一些法则来帮助。
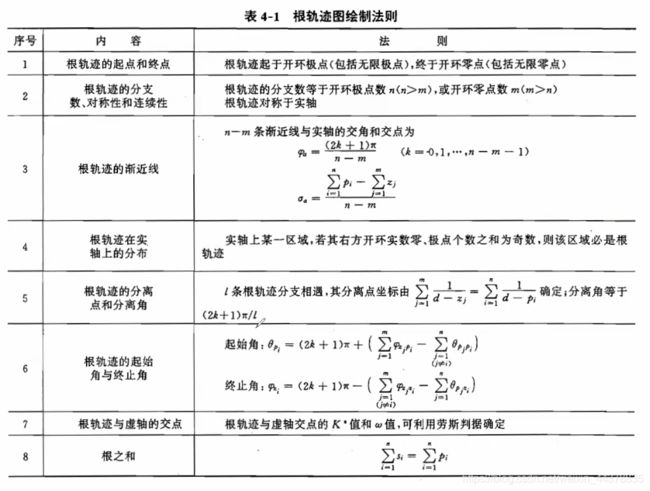
C 绘制根轨迹的法则
C.a 根轨迹法则介绍
1、首先讨论负反馈系统在开环增益 或根轨迹增益 变 化时的根轨迹的绘制法则,又称常规根轨迹的绘制法则;
2、当其他参数变化时,只要适当变换,常规根轨迹的法 则仍然可用;
3、虽然用这些法则绘制的根轨迹不够精确,但基本可以 满足工程上的应用;
4、若需要更精确的根轨迹可以利用相方程,对根轨迹进 行修正,或利用计算机绘制根轨迹图。
C.b 根轨迹法则(常规根轨迹)
闭环极点与根轨迹增益 K ∗ K^* K∗、开环零点和极点有关。
1 根轨迹的分支数等于特征方程的阶数
当开环根轨迹增益变化时,共有n个极点在复平面上移动, 共形成n条轨迹。所以,根轨迹的分支数等于开环极点的个数。
2. 根轨迹是连续的且对称于实轴
在开环零、极点确定的情况下,闭环特征根是开环根轨迹 增益的连续函数。由于特征方程的系数是实数,所以特征根或 是实数,或是共轭复数,即根轨迹对称于实轴。
3. 根轨迹起始于开环极点,终止于有限的开环零点或无穷远处。
所谓根轨迹的起点和终点,是分别指当 K ∗ K^* K∗等于零和无穷 大时根轨迹的位置。
(1) 根轨迹的起点
闭环特征方程
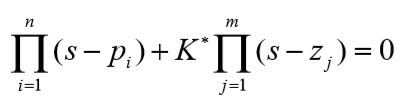
当 K ∗ = 0 K^*=0 K∗=0时,
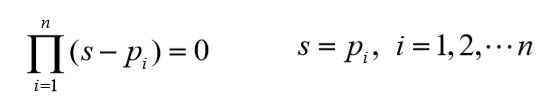
即当根轨迹增益为零时,开环极点就是闭环极点,所以,根轨迹 起始于开环极点。
(2) 根轨迹的终点
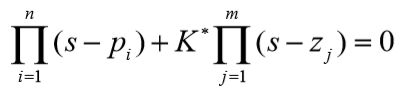
令 s = 1 q s=\frac{1}{q} s=q1,得到等价方程:

当 K ∗ → ∞ K^*\rightarrow\infty K∗→∞时,等价方程为:

有n-m个根等于0,m个根等于 1 z j \frac{1}{z_j} zj1

上述等价方程的根对应于
![]()
根轨迹终止于有限的开环零点(有限零点)或无穷远处(无限零点),其中无穷远处终点个数为极点个数-零点个数。
4. 实轴上的根轨迹
设系统有n个开环极点和m个开环零点(分布对称于实轴的)。
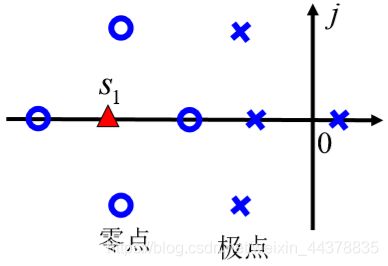
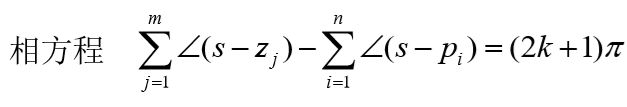
将实轴上某点s1代入相方程,得

m1 — 点 s1 右侧实轴上零点的个数
n1 — 点 s1 右侧实轴上极点的个数。
若 ( m 1 − n 1 ) (m_1-n_1) (m1−n1)为奇数,则点 s1 是根轨迹上的点
实轴上某一区域,若其右边开环实轴零、极点的个数之和 为奇数,则该区域必是根轨迹。
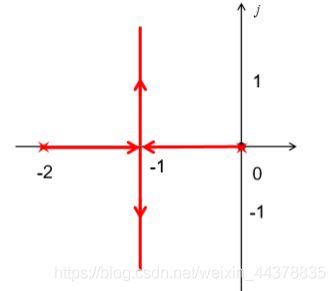
( − ∞ , − 4 ) (-\infty,-4) (−∞,−4)右边有两个极点一个零点; ( [ − 2 , 0 ] ) ([-2,0]) ([−2,0])右边只有一个极点。
由法则一,根轨迹起始于开环极点。终止于有限的开环零点或无穷远。得到根轨迹如图红箭头。
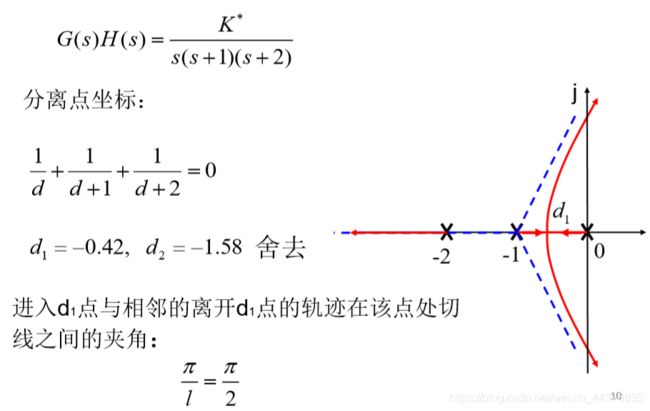
5. 根轨迹的分离点(或会合点)坐标
做题时使用试探法求解。
两条或两条以上的根轨迹在s平面上相遇又立即分离的点称 为根轨迹的分离点(或汇合点)。
闭环特征多项式:

若两条或两条以上的根轨迹在复平面上某个点d处相遇,则点d 为特征多项式的一个重根。即满足
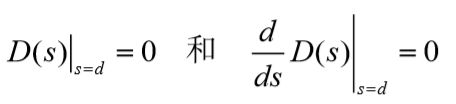
由此可得分离点(或汇合点)的必要条件为
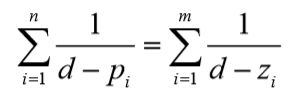

系统有两个极点就有两个根轨迹,一个从0出发,一个从-2出发,在d1点汇合,然后分别进入复平面,又在d2点汇合,然后再分开,一个趋于-3,一个趋于负无穷。
6. 根轨迹的渐近线
若开环极点数n大于开环零点数m,则当 K ∗ K^* K∗趋于无穷大时,将有 n-m 条根轨迹趋于无穷远处。可以证明这n-m条趋于无穷远的轨迹将趋近于n-m条直线,这些直线称为根轨迹的渐近线。
渐近线与正实轴的夹角为 :
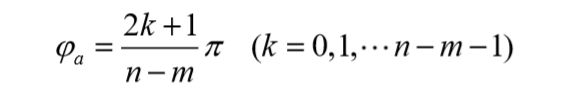
渐近线与实轴的交点横坐标为

p i p_i pi开环极点; z i z_i zi开环零点。


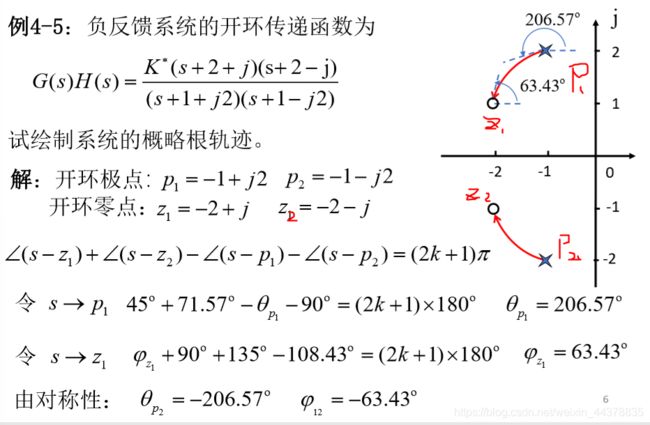
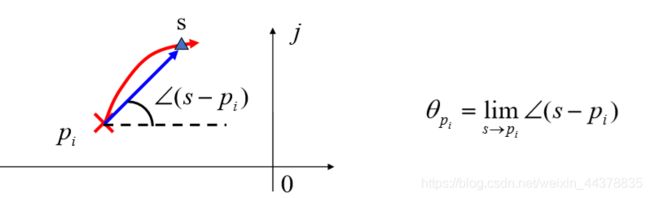
7根轨迹的起始角和终止角
起始角:根轨迹离开开环极点处的切线与正实轴的夹角。

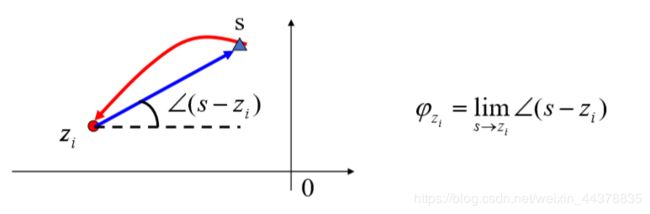
终止角:根轨迹进入开环零点处的切线与正实轴的夹角。

8分离角与会合角
设n阶系统在根轨迹增益 K ∗ = K d K^*=K_d K∗=Kd时,有l个闭环重极点,即 s i = d ( i = 1 , 2 , . . . , l ) s_i=d(i=1,2,...,l) si=d(i=1,2,...,l),其余 n − l n-l n−l个闭环极点为 s i ( i = l + 1 , l + 2 , . . . , n ) 。 s_i(i=l+1,l+2,...,n)。 si(i=l+1,l+2,...,n)。
汇合角 φ d \varphi_d φd :根轨迹进入汇合点处的切线与实轴正方向的夹角
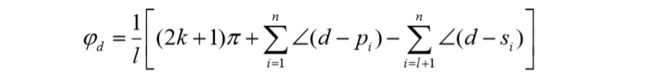
分离角 θ d \theta_d θd :根轨迹离开分离点处的切线与实轴正方向的夹角。
将以上计算公式归纳为如下便于记忆的法则:
若有 l l l 条根轨迹进入 d d d 点,必有 l l l条根轨迹离开 d d d点; l l l 条进 入 d d d 点的根轨迹与 l l l 条离开 d d d 点的根轨迹相间隔(如图1为进2为出,进出相互间隔);任一条进入 d d d 点的根轨迹与相邻的离开 d d d 点的根轨迹方向之间的夹角为 π / l \pi/l π/l
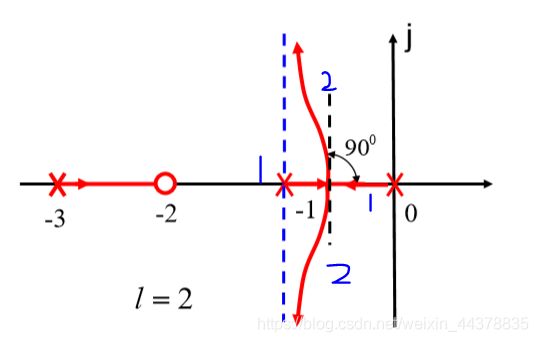
π / l = π / 2 = 90 ° \pi/l=\pi/2=90° π/l=π/2=90°
9. 根轨迹与虚轴的交点坐标
若根轨迹与虚轴相交,交点对应的根轨迹增益 K ∗ K^* K∗和角频率 w w w可用劳斯判据或令闭环特征方程中的 s = j w s=jw s=jw(虚轴上实部为零), 然后 分别令实部和虚部为零求得交点和对应的 K ∗ K^* K∗值。
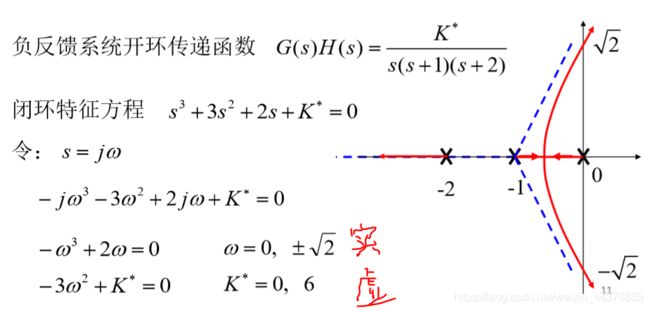
w = 0 , K ∗ = 0 w=0,K^*=0 w=0,K∗=0为根轨迹的起点 w = ± 2 , K ∗ = 6 w=\pm\sqrt{2},K^*=6 w=±2,K∗=6,为终点,超过6则到了右半平面,不稳定。
实际上若根轨迹与虚轴相交,则表示闭环系统存在纯虚根,这意味着该数值使闭环系统处于临界稳定状态。
10. 根之和与根之积
当系统的开环传递函数分母和分子的次数满足 n > m + 2 n>m+2 n>m+2,则系统开环极点之和总是等于系统闭环特征根之和。
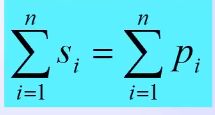
在开环极点确定的情况下,这是一个不变的常数。 所以,当开环增益K 增大时,若闭环某些根在S平 面上向左移动,则另一部分根必向右移动,如一个根在(0,0)一个根在(-2,0),若(0,0)变化为(-0.1,0),则(-2,0)也就会变化为(-1.9,0)。
D 广义根轨迹
广义根轨迹是指根轨迹参数除了开环增益之外的 所有根轨迹。通常,将负反馈系统中K*变化时 的根轨迹叫做常规根轨迹。
D.a 参数根轨迹
对闭环特征方程
进行等效变换,将其写为如下形式:

其中, A A A为除 K ∗ K^* K∗外系统任意的变化参数。
D.a.a 开环零点变化时的根轨迹

(1)两个系统的闭环特征方程相同;
(2)原系统开环零点是 1 / T d 1/T_d 1/Td ,而 T d T_d Td是等效系统的开环增益;
(3)等效系统开环增益变化的根轨迹,就是原系统开环零点变化的根轨迹。
D.a.b 开环极点变化时的根轨迹
D.b 附加开环零点的作用
在控制系统设计中,常用附加位置适当的开环零点的方 法来改善系统性能。
1、对系统稳定性的改善
设系统开环传递函数为:

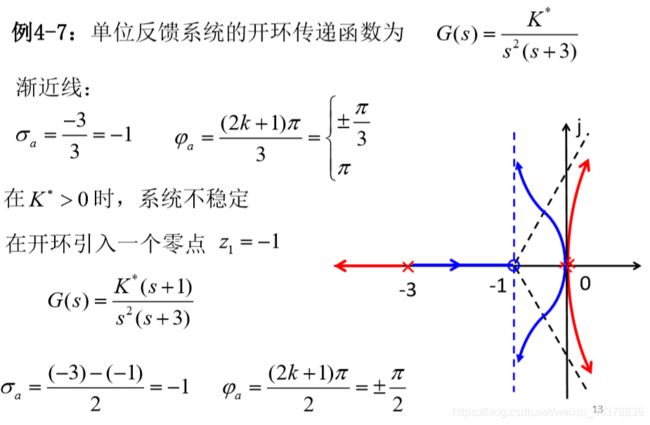
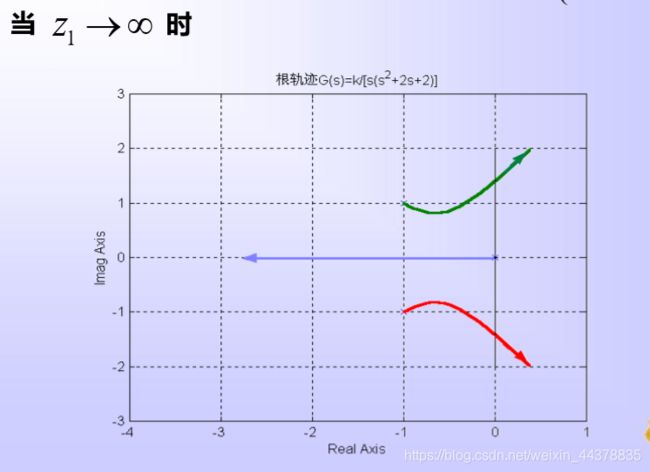
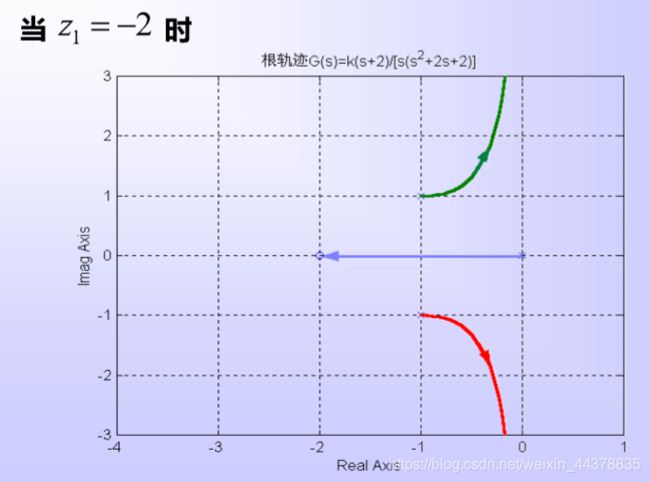
式中Z1为附加的开环实数零点。取z1 为不同值时,根轨 迹如下:
 |
 |
 |
 |
分析:由图可见,当开环极点位置不变,而在系 统中附加开环负实数零点时,将使系统的根 轨迹图发生趋向附加零点方向的变形,而且 这种影响将随开环零点接近坐标原点的程度 而加强。如果附加的开环零点不是负实数零 点,而是具有负实部的共轭零点,那么它们的作用与负实数零点的作用完全相同。
当根轨迹增益为 K ∗ K^* K∗时, 复数极点S1 和S2 为闭 环主导极点,实数极点 S3距虚轴较远,为非 主导极点。在这种情况 下,闭环系统近似为一 个二阶系统,具有良好 的动态性能。
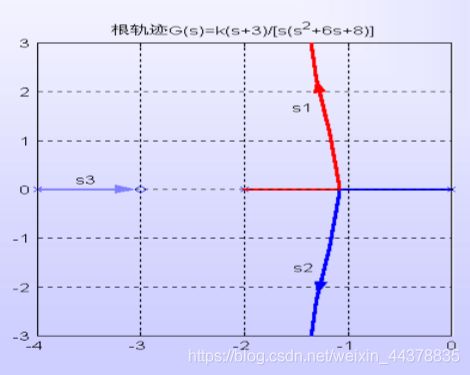
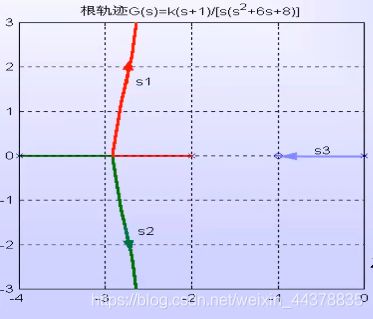
在图中,实数极点 s 3 s_3 s3为闭环主导极点,此时系 统等价于一阶系统,其动 态过程虽然可能单调, 但却具有较慢的响应速度 和较长的调节时间。也就 是说,此时稳态性能优于 z = − 3 z=-3 z=−3时,但动态性能 却变差了。
结论: 只有当附加零点相对原有系统开环极点的位置 选配适当,才有可能使系统的稳定性和动态性能同 时得到明显的改善。
E 系统性能的分析
1、稳定性
如果闭环极点全部位于s左半平面,则系统一定是 稳定的,即稳定只与闭环极点位置有关,而与闭环 零点位置无关。
2、运动形式
如果闭环系统无零点,且闭环极点均为实数极 点,则时间响应一定是单调的; 如果闭环极点均为复数极点,则时间响应一般是 振荡的。
3、超调量
超调量主要取决于闭环复数主导极点的衰减率 σ 1 / w d = ζ / 1 − ζ 2 \sigma_1/w_d=\zeta/\sqrt{1-\zeta^2} σ1/wd=ζ/1−ζ2 ,并与其它闭环零、极点接 近坐标原点的程度有关。
4、调节时间
调节时间主要取决于最靠近虚轴的闭环复数 极点的实数绝对值 σ 1 = ζ w n \sigma_1=\zeta w_n σ1=ζwn ,如果实数极点距虚 轴最近,并且它附近没有实数零点,则调节时间 主要取决于该实数极点的模值。
5、实数零、极点影响。
零点减小系统阻尼,使峰值时间提前,超调量 增大;极点增加系统阻尼,使峰值时间滞后,超调 量减小。它们的作用,随着其本身接近坐标原点的 程度而加强。
6、偶极子及其处理
如果零、极点之间的距离比它们本身模值小 一个数量级,则它们就构成了偶极子。远离原点 的偶极子,其影响可略;接近原点的偶极子,其 影响必须考虑。
7、主导极点
在s平面上,最靠近虚轴而附近又无闭环零点 的一些闭环极点,对系统性能影响最大,称为主 导极点,凡比主导极点的实部大3-6倍以上的其他 闭环零、极点,其影响均可忽略。