描述子-FPFH&SHOT&NARF

1.shot描述子

在3D点云目标识别中，除了传统的利用二维图像来辅助识别，然后映射到3D的方式；学术界在十几年前就开始研究3D点云的特征描述子。

本文主要详解意大利博洛尼亚大学教授提出的SHOT（Signature of Histogram of  Orientation）http://www.vision.deis.unibo.it/SHOT。

1、3D特征描述子

图1.1 3D描述子编码通用规则

　　描述子的构建一般分为两个过程特征编码（Signature）和直方图统计（Histogram），特征编码是关键，直方图是表述特征的分布情况，增强特征的鲁棒性（概率的角度）。

　　Signature：类似于2D图像的特征描述子，对特征点附近的信息进行编码，图像是圆形或矩形Patch中的灰度、梯度变化信息。相似的，点云特征描述子就是对点领域附近的几何信息和颜色、纹理信息进行编码；几何信息主要有K-近邻点（或者support）的法线方向、夹角、曲率等；

　　Histogram：有了K-邻域内（支撑区域）点的一系列特征描述子，采用对每个子区域进行特征统计的思路，可以构建出整个支撑区域的直方图特征。

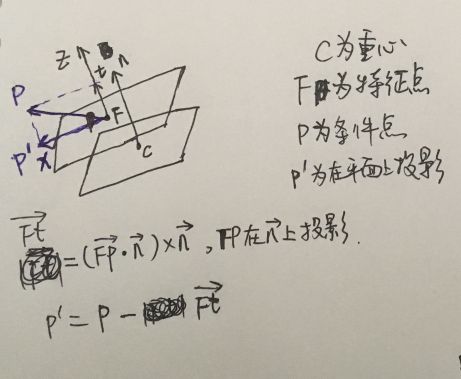
2、局部坐标系（Local Reference Frame）

　　有了K-近邻点后，怎么去提取特征点的几何信息呢？？文献中一般是采用局部坐标系（Local Reference Frame）来作为几何信息的参考原点。

　　

　　图1.2 Local Reference Frame

　　局部坐标系的Z轴确定方式：对K-近邻点拟合平面，平面法向量作为局部坐标系的Z轴，Z轴的方向由法向量n和K-近邻法向量均值的方向相同。法向量计算理论参考

　　SHOT在计算Z轴的时候，加了距离权重，

　　局部坐标系的X轴确定方式：计算法向量n与每个近邻的点乘，找夹角最大的的P（即cos最小），然后计算P到过特征点F点平面的投影P′。特征点F与投影P′组成的方向为X轴方向。

　　局部坐标系的Y轴确定方式：x轴和Z轴叉乘得到。

　　需要注意，局部坐标系中的重心一般和特征点不是同一个点。

3、SHOT直方图编码

图1.3 SHOT特征

　　借鉴2D图像的SIFT特征，邻域内法向量整体的直方图特征鲁棒性较低，采用局部直方图形式进行编码。SHOT将整个邻域划分为32小块，纬度2分，半径2分，经度8分。

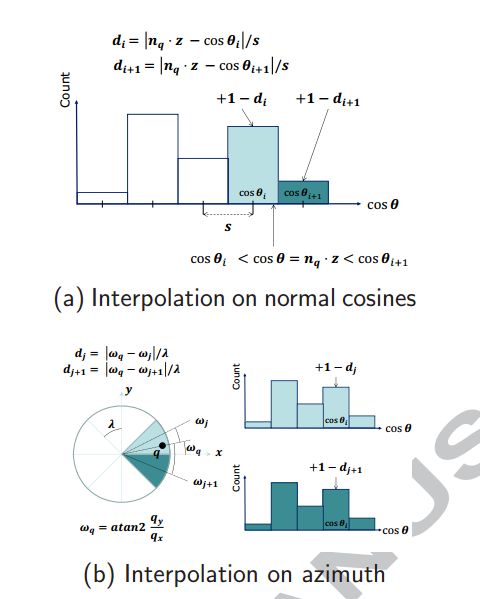
　　计算每个近邻点相对于法向量的夹角（特征值），对每个小块内的特征值构建直方图（11级），累积直方图采用插值的形式（这里理解起来相对困难，编码也很复杂，看了PCL的源码，费心），角度差值，纬度方向插值、经度方向插值和半径方向插值。

　　起始就是定义一个规则，判断当前特征值落在哪个区间里面，每个曲面的特征值按照下图方式计算。最后得到的特征向量为32x11 = 352维。

图1.4 插值方式

4、SHOT描述在纹理上的扩展

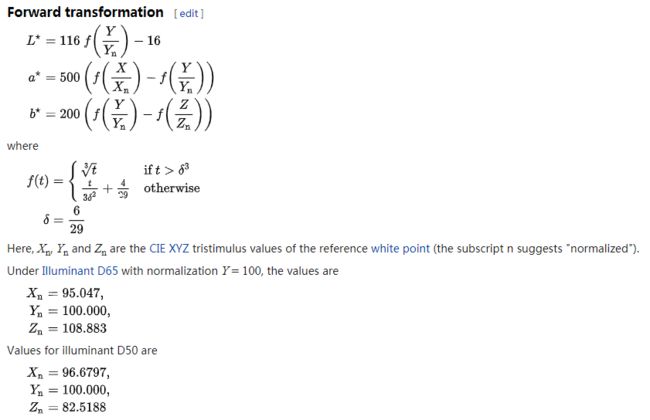
　　由于最初提出的SHOT描述子是不针对纹理和颜色信息的，单纯的几何信息编码影响识别的准确率，因此后来SHOT加入了颜色信息。SHOT中的颜色编码主要是LAB空间(CIELAB计算)中的颜色；直方图31级，因此颜色描述子长度32x31 = 992;添加颜色信息的SHOT描述子共1344维。

　　一般颜色域都是RGB或者HSV（色度、饱和度、亮度），lab空间是开发出来近似人眼视觉系统的，色域比RGB大得多。感觉Lab只有在做为颜色标定或者参考时才用的上，没想到这里用了，应该是为表达颜色更准确。

　　RGB需要先转换到XYZ，然后XYZ转LAB。颜色空间转换代码

2.EPFH：

点特征的描述子一般是基于点坐标、法向量、曲率来描述某个点周围的几何特征。用点特征描述子不能提供特征之间的关系，减少了全局特征信息。因此诞生了一直基于直方图的特征描述子：PFH--point feature histogram（点特征直方图）。

2.PFH的原理

PFH通过参数化查询点和紧邻点之间的空间差异，形成了一个多维直方图对点的近邻进行几何描述，直方图提供的信息对于点云具有平移旋转不变性，对采样密度和噪声点具有稳健性。PFH是基于点与其邻近之间的关系以及它们的估计法线，也即是它考虑估计法线之间的相互关系，来描述几何特征。

为了计算两个点（ ps is defined as the source point and pt as the target point）及其相关法线之间的偏差，在其中一个点上定义了一个固定坐标系。

使用上图的uvw坐标系，法线ns，nt之间的偏差可以用一组角度表示

d是两点之间的欧氏距离， ，利用α,φ,θ,d，四个元素可以构成PFH描述子。

问题来了，PFH翻译成点特征直方图，四个元素和直方图有什么关系？

首先计算查询点Pq近邻内的对应的所有四个元素，如图所示，表示的是一个查询点(Pq) 的PFH计算的影响区域，Pq 用红色标注并放在圆球的中间位置，半径为r， (Pq)的所有k邻元素（即与点Pq的距离小于半径r的所有点）全部互相连接在一个网络中。最终的PFH描述子通过计算邻域内所有两点之间关系而得到的直方图，因此存在一个O(k) 的计算复杂性。 

为了创建最终的直方图，将所有四元素组以统计的方式放入一个直方图中，这个过程首先把每个特征值范围划分为b个子区间，并统计落在每个子区间的点数量，前三个元素均是角度，都和法向量有关系，可以将三个元素标准化并放到同一个区间内。

横坐标表示角度，纵坐标表示区间内点云的数量。

3.FPFH的由来

具有n个点的点云p的点特征直方图的理论计算复杂度为o（nk^2），其中k是点云p中每个点p的邻近数。在密集点邻域中计算点特征柱状图可以表示映射框架中的主要瓶颈之一。本节提出了PFH公式的简单化，称为快速点特征直方图（FPFH:fast point feature histograms），它将算法的计算复杂度降低到O（NK），同时仍然保留了PFH的大部分判别能力。

4.FPFH的原理

step1，只计算每个查询点Pq和它邻域点之间的三个特征元素（参考PFH），在这里不同于PFH：PFH是计算邻域点所有组合的特征元素，而这一步只计算查询点和近邻点之间的特征元素。如下图，第一个图是PFH计算特征过程，即邻域点所有组合的特征值（图中所有连线，包括但不限于Pq和Pk之间的连线），第二个图是step1中计算内容，只需要计算Pq（查询点）和紧邻点（图2中红线部分）之间的特征元素。可以看出降低了复杂度我们称之为SPFH（simple point feature histograms）。

 

step2，重新确定k近邻域，为了确定查询点Pq的近邻点Pk的SPFH值、查询点Pq和近邻的距离以及k的数值（一般使用半径kdtree搜索，只能确定某半径范围内的近邻点，不能确定具体的查询点与近邻的距离、k数值----PS:应该是这样，不过重新确定k近邻主要还是计算查询点Pq的近邻点Pk的SPFH值），则

Wk权重，一般为距离。

5.二者区别和联系

（1）FPFH没有对近邻点所有组合进行计算可能漏掉一些重要点对

（2）PFH特征模型是对查询点周围精确的邻域半径内，而FPFH还包括半径r范围以外的额外点对（不过在2r内，这是由于计算SPFH(Pk)导致的）

（3）FPFH降低了复杂度，可以在实时场景中使用

（4）因为重新计算权重，所以FPFH结合SPFH值，重新获取重要的紧邻点对几何信息

（5）在FPFH中，通过分解三元组（三个角特征）简化了合成的直方图，即简单地创建b个相关的的特征直方图，每个特征维数（dimension）对应一个直方图（bin），并将它们连接在一起。pcl默认，in PFH assume the number of quantum bins (i.e. subdivision intervals in a feature’s value range),bins（b）=5即子区间数量，三个角特征元素，3^5=125,也就是一个查询点就有125个子区间，PFHSignature125的由来。这样有一个问题：对于点云特别是稀疏点云来说，很多区间存在0值，即直方图上存在冗余空间。因此，在FPFH中，通过分解三元组（三个角特征）简化了合成的直方图，即简单地创建b个不相关的的特征直方图，每个特征维数（dimension）对应一个直方图（bin），并将它们连接在一起。pcl默认FPFH的b=11，3*11=33，也就是FPFHSignature33的由来。