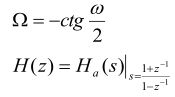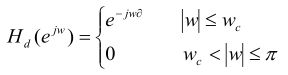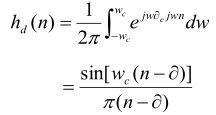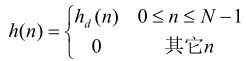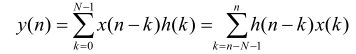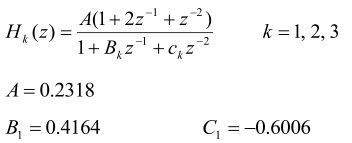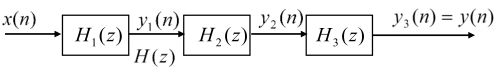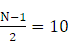数字信号处理：设计滤波器及比较 双线性变换法设计 IIR 滤波器 窗口法设计 FIR 滤波器
实验4 用双线性变换法设计 IIR 滤波器
实验目的
熟悉模拟 Batterworth滤波器设计和用双线性变换法设计IIR数字滤波器的方法。
实验原理
利用双线性变换设计 IIR滤波器，首先要设计出满足指标要求的模拟滤波器的传递函数
，然后由
通过双线性变换可得所要设计的 IIR滤波器的系统函数
。
如果给定的指标为数字滤波器的指标，则首先要转换成模拟域指标。
- 低通数字滤波器设计
数字域与模拟域关系
- 高通数字滤波器设计
数字域与模拟域关系
实验内容及要求
- 编写用双线性变换法设计 Batterworth 低通 IIR数字滤波器的程序，要求通带内频率低于
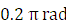时，容许幅度误差在
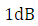之内，频率在
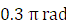到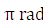
之间的阻带衰减大于 15dB。其中要求参数
,
, 
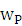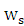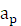和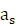
可由键盘输入。 - 以
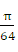为采样间隔，在屏幕上打印出数字滤波器的频率区间
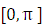上的幅频响应特性曲线( 
)。 - 在屏幕上打印出
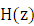的分子，分母多项式系数。
实验结果
实验代码如下：
close all
clear all
%可输入
%wp=input('wp: '); %0.2*pi
%ws=input('ws: '); %0.3*pi
%Rp=input('Rp: '); %1
%Rs=input('Rs: '); %15
wp=0.2*pi;
ws=0.3*pi;
Rp=1;
Rs=15;
Fs=1;
wp1=2*Fs*tan(wp/2); %归一化
ws1=2*Fs*tan(ws/2);
[N,Wn]=buttord(wp1,ws1,Rp,Rs,'s'); %巴特沃斯滤波器
%wp1模拟滤波器通带截止频率 wp2阻带截止频率 Rp通带最大衰减 Rs阻带最大衰减
%N最小阶数 Wn滤波器固有频率
[Z,P,K]=buttap(N); %低通原型模拟滤波器
%Z P K 零点矢量 极点矢量 增益
[Bap,Aap]=zp2tf(Z,P,K);
%Bap Aap 传递函数分子和分母的多项式系数
[b,a]=lp2lp(Bap,Aap,Wn); %b a 所设计的模拟滤波器系统函数的分子 分母系数
[bz,az]=bilinear(b,a,Fs); %bz az 所设计的数字滤波器系统函数的分子 分母系数
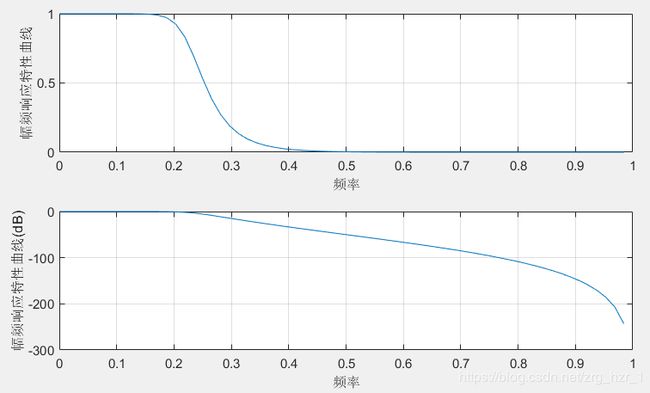
[H,W]=freqz(bz,az,64); %freqz函数自动将64个点均匀设置在[0~pi]之间 计算出64个点的频率响应存放于H向量中，64个频率存放在W向量中
subplot(2,1,1);
plot(W/pi,abs(H)); %幅频特性
grid;
xlabel('频率');
ylabel('幅频响应特性曲线');
subplot(2,1,2);
plot(W/pi,20*log10(abs(H)));%幅频特性(dB)
grid;
xlabel('频率');
ylabel('幅频响应特性曲线(dB)');
bz
az
实验结果如下：
bz =
0.0007 0.0044 0.0111 0.0148 0.0111 0.0044 0.0007
az =
1.0000 -3.1836 4.6222 -3.7795 1.8136 -0.4800 0.0544
实验5 用窗口法设计 FIR 滤波器
实验目的
了解一个实际滤波器设计过程，加深掌握用窗口法设计FIR 滤波器的原理和窗函数对滤波器性能的影响。
实验原理
设低通滤波器的时延为
，即：
则
这是一个以
为中心的偶对称的无限长非因果序列。这样一个无限长的序列怎样用一个有限长序列去近似呢？最简单的办法就是直接截取它的一段来代替它。例如把 
到 
的一段截取来作为
，但是为要保证所得到的是线性相位滤波器。必须满足
的对称性，所以时延 
应该取
长度的一半，即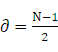 
即
但是一般来说，窗口函数并不一定是矩形函数，可以在矩形以内还对 
作一定的加权处理，因此，一般可以表示为
这里
就是窗口函数。这种对理想单位取样响应加窗的处理对频率响应会产生以下三点影响：
（1）使理想特性不连续的边沿加宽，形成一过渡带，过渡带的宽度取决于窗口频谱的主瓣宽度。
（2）在过渡带两旁产生肩峰和余振，它们取决于窗口频谱的旁瓣；旁瓣越多，余振也越多；旁瓣相对值越大，肩峰则越强。
（3）增加截取长度
，只能缩小窗口频谱的主瓣宽度而不能改变旁瓣的相对值；旁瓣与主瓣的相对关系只决定于窗口函灵敏的形状。因此增加 
，只能相对应减小过渡带宽。而不能改变肩峰值。肩峰值的大小直接决定通带内的平稳和阻带的衰减，对滤波器性能有很大关系。例如矩形窗的情况下，肩峰达
，致使阻带最小衰减只有 
分贝，这在工程上往往是不够的。怎样才能改善阻带的衰减特性呢？只能从改善窗口函数的形状上找出路，所以希望的窗口频谱中应该减少旁瓣，使能量集中在主瓣，这样可以减少肩峰和余振，提高阻带的衰减。而且要求主瓣宽度尽量窄，以获得较陡的过渡带，然而这两个要求总不能兼得，往往需要用增加主瓣宽度带换取决瓣的抑制，于是提出了海明窗、凯宽窗、切比雪夫窗等窗口函数。
实验内容及要求
用改进余弦窗设计一个FIR 线性相应相位低通数字滤波器，已知 
, 
。编写调试程序，要求在幕幕上显示出单位脉冲响应 
的数值，画出其幅度响应 
的曲线。
实验结果
close all
clear all
wc=0.5*pi;
N=21;
r=(N-1)/2;
n=0:N-1;
hdn=sin(wc*(n-r))/pi./(n-r);
if rem(N,2)~=0;
hdn(r+1)=wc/pi;
end
wn=hamming(N);
h=hdn.*wn';
H=fft(h,512);
w=2*[0:511]/512;
subplot(3,1,1);
stem(n,h,'.');
title('h(n)');
xlabel('n');
ylabel('幅度');
subplot(3,1,2);
plot(w,abs(H));
title('H(exp(jw))');
xlabel('w/pi');
ylabel('幅度');
subplot(3,1,3);
plot(w,20*log10(abs(H)));
title('H(exp(jw))');
xlabel('w/pi');
ylabel('幅度(db)');
实验6 IIR 和 FIR 滤波器过滤信号的实现及比较
实验目的
1、 掌握数字滤波器的计算机仿真方法。
2、 通过观察对实际心电图信号的滤波作用，获得数字滤波的感性知识。
实验原理
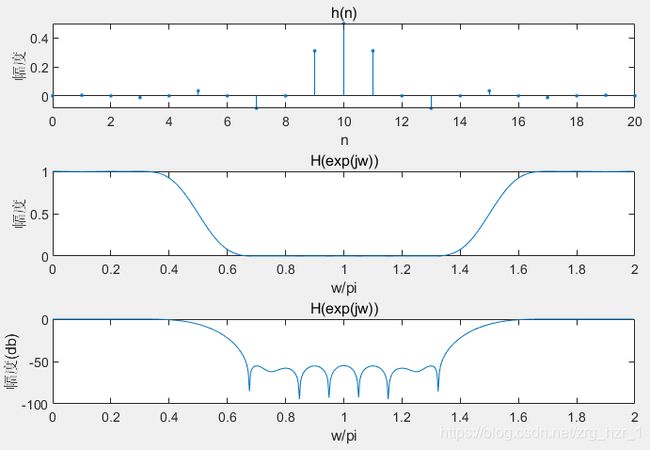
若
是因果FIR 滤波器的单位脉冲响应，其长度为N，当输入为 
时，输出序列
为：
取
为低通滤波器 
，截止频率 
，采用海明窗设计出 
。
若 
是 
滤波器，在通常内频率低于 
时，最大衰减小于 
；在阻带内 
频率区间上，最小衰减大于
。用双线性变换法设计得到 Batterworth滤波器系统函数 
为：
式中
滤波器
由三个二阶滤波器
, 
和
级联组成，如下图所示：
可得
当
时， 
实验内容及要求
1、 编写FIR滤波器仿真程序，计算其对心电图信号采样序列
的响应序列
。
2、 编写 IIR滤波器仿真程序，计算其对心电图信号采样序列 
的响应序列 
。
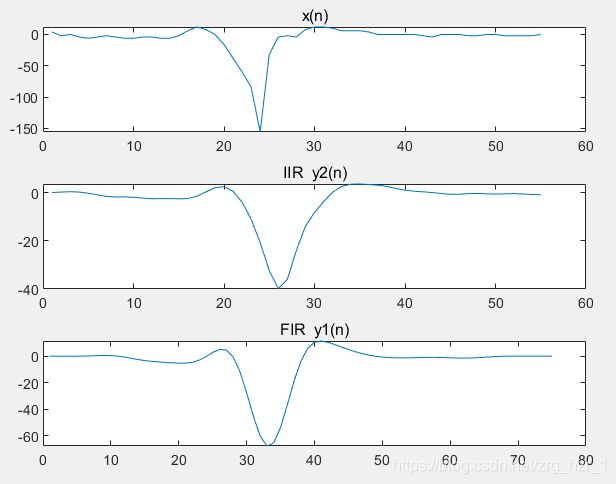
3、 在通用计算机上运行仿真滤波器程序，在屏幕上打印出 
、
和
，并进行比较。
实验结果
close all
clear all
x=[4 -2 0 -4 -6 -4 -2 -4 -6 -6 -4 -4 -6 -6 -2 6 12 8 0 -16 -38 -60 -84 -90-66 -32 -4 -2 -4 8 12 12 10 6 6 6 4 0 0 0 0 0 -2 -4 0 0 0 -2 -2 0 0 -2 -2 -2 -2 0];
A=0.2318;
B1=0.4164;
C1=-0.6006;
B2=0.3093;
C2=0.1888;
B3=0.2692;
C3=-0.0349;
a1=[1 B1 C1];
b1=[A 2*A A];
a2=[1 B2 C2];
b2=[A 2*A A];
a3=[1 B3 C3];
b3=[A 2*A A];
y1=filter(b1,a1,x);
y2=filter(b2,a2,y1);
y3=filter(b3,a3,y2);
y=y3;
subplot(3,1,1)
plot(x);
title('x(n)');
subplot(3,1,2)
plot(y);
title('IIR y2(n)');
subplot(3,1,3)
N=21;
Window = hamming(N);
wc=0.2*pi;
hn=fir1(N-1,wc/pi,Window);
yn=conv(x,hn);
plot(yn);
title('FIR y1(n)');
FIR 延迟 
实验总结
- 数字滤波器作用：利用离散时间系统的特性对输入信号波形（或频谱）进行加工处理，把输入序列x(n)变换成一定的输出序列y(n)从而达到改变信号频谱的目的。
- 运算量 FIR 大原因：得到严格的线性相位，阶数高，运算次数高，延时比较大。
- FIR 存储速度更快： FIR 可以采用非递归结构；可以利用快速傅里叶算法。
通过本次试验，我明白了 FIR 和IIR的滤波原理，并了解了它们的区别。