数字信号处理5：FIR滤波器设计

之前的一系列博客中，详细分解了从卷积到FFT的相关知识，不过那些属于理论，是为了让我们清楚认识到信号处理的本质。本篇博客将会详细讲解数字信号处理最广泛的应用——滤波器。

注意，本章所采用的dB标准为

$$dB=20log\frac{V}{V_{base}}$$

其中，$V_{base}$表示某种作为标准的幅度值，它或者是电平，或者是信号振幅。在这里，我们通常将它认为是原信号的“大小”，这个大小不光可以是信号在时域的幅度，也可以是在频域的频率分量的大小。

1. 滤波器初识

滤波器，如同字面意思是过滤信号的某些频率分量。入门时书上最常说的几种滤波器，比如低通、带通、高通、带阻等滤波器。如下是一个低通滤波器。

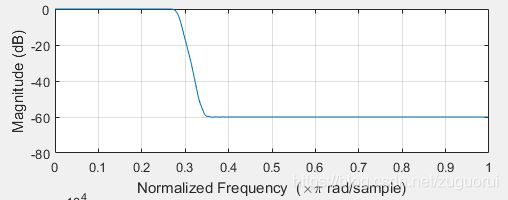
它将信号中的中高频分量降低了60dB。按照dB的定义，也就是中高频信号的幅度降低为原来的0.001倍。

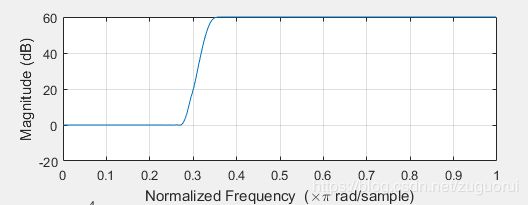
实际上，更为广泛的滤波器，并不只有“滤”的作用，它同样还可以对某些频段进行增强，如下滤波器：

它将信号中的中高频部分提高了60dB。按照dB的定义，也就是中高频信号的幅度提高到原来的1000倍。

2. 最直观的滤波方式：频域滤波

回想一下《数字信号处理2：傅里叶变换》博客中讲的傅里叶变换的直观理解那部分。傅里叶变换之后的结果是一组虚数，这组虚数的相位反应的就是原信号中各频率正弦波的相位，而这些虚数的绝对值某种程度上反应了对应频率的信号在原始信号中的大小。所以，我们只要对频域上的这些虚数的绝对值进行调节，再作傅里叶逆变换，即可以调整原信号中的某些频率分量的大小，也就成为了滤波的一种手段。步骤通常如下：

1. 对信号加窗
2. 对加窗之后的结果作傅里叶变换。
3. 根据你的目的对傅里叶变换结果的某些频率上的分量调节绝对值。
4. 将调节完毕后的结果作傅里叶逆变换。

这便是频域滤波。

3. 傅里叶变换中的加窗

在上一部分中提到了对信号进行加窗，为什么要进行加窗操作？加的又是什么窗？

要理解加窗的意义，有两种方式。

首先，回想一下博客《数字信号处理2：傅里叶变换》中对傅里叶变换的推导过程，对于傅里叶变换所做的所有推导，都是基于无限长周期信号进行的。我们假设用来做傅里叶变换的信号是从周期信号中截取的一整个周期。所以，如果这段信号前后进行拼接成我们假想的周期信号后，中间没有突变点（包括斜率突变、断点等情况），那么直接进行傅里叶变换是没有问题的。而如果前后进行拼接后，中间出现了突变点，那么从直觉就可以知道，这个突变点中包含了相当多的频率分量。但单从我们截取的这段信号来说，是不应该有这些多余的频率分量的。

下面举个例子：

构造一个频率为20的周期信号。首先，我们让这段信号有整数个周期。使用matlab。

T = 200;

x = [0:1:T-1];
sinWave = sin(2 * pi / T * 20 * x);
plot(x, sinWave);
title("频率为20的正弦波");
b = fft(sinWave);
plot(x, abs(b));
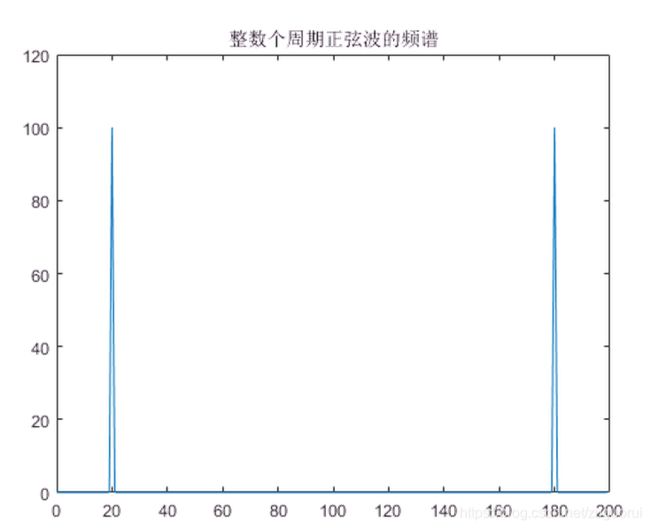
title("整数个周期正弦波的频谱")

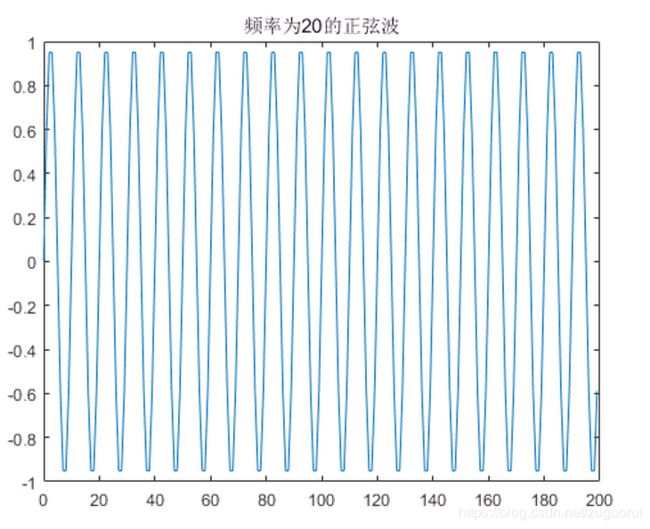
代码中生成的sin波是完整的20个周期，采样点200个，周期是10。绘制出来的图像如下：

可以看到，频谱上仅在周期为20的位置有值。

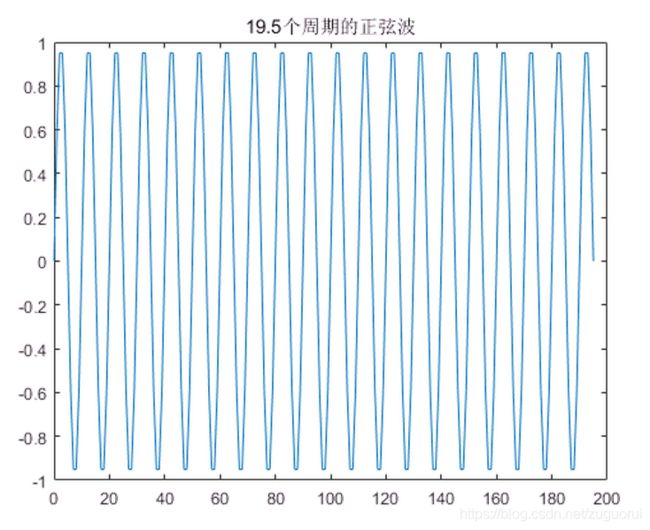
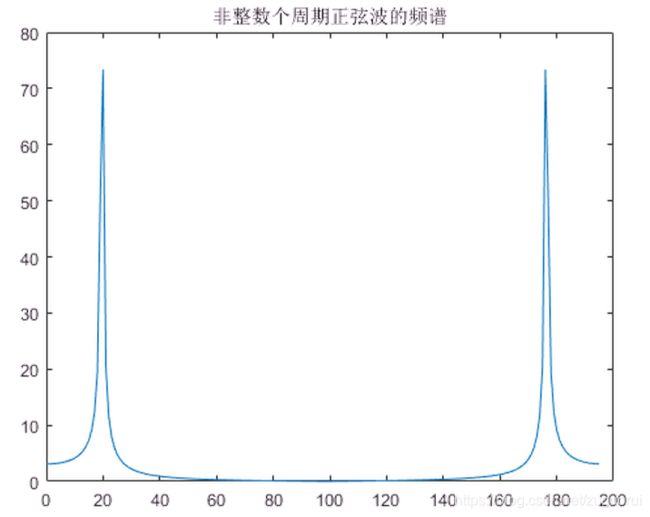
如果不给整数个周期。比如只给19.5个周期。显然，这样的信号前后拼接成周期信号后，必然是会有突变点的。

x = [0:1:195];
sinWave = sin(2 * pi / T * 20 * x);
plot(x, sinWave);
title("19.5个周期的正弦波");
b = fft(sinWave);
%b = circshift(b', fix(length(sinWave) / 2))';
plot(x, abs(b));
title("非整数个周期正弦波的频谱")

可以看到，这时在频率20周围出现了其他的频率分量，这就是频率泄漏。

实际运用中，一段信号通常有很多频率的正弦波组成，我们不能保证总是能截取到整数个周期，因此，通过加窗的方式，我们使信号两端加一个渐缓的过程，使得拼接成周期信号后，没有突变点。

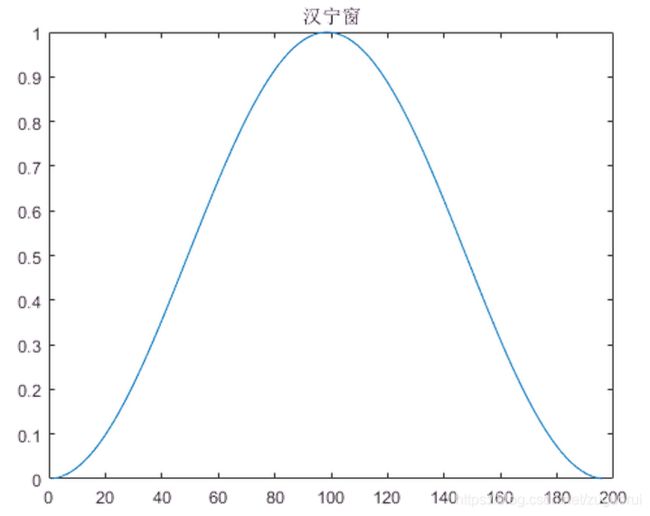
举一个例子：汉宁窗。它的形状如下：

对于上面提到的非整数个周期的信号，我们对其进行加窗操作：

x = [0:1:195];
window = hanning(length(x))';
plot(window);
title("汉宁窗");
sinWave = sin(2 * pi / T * 20 * x) .* window;
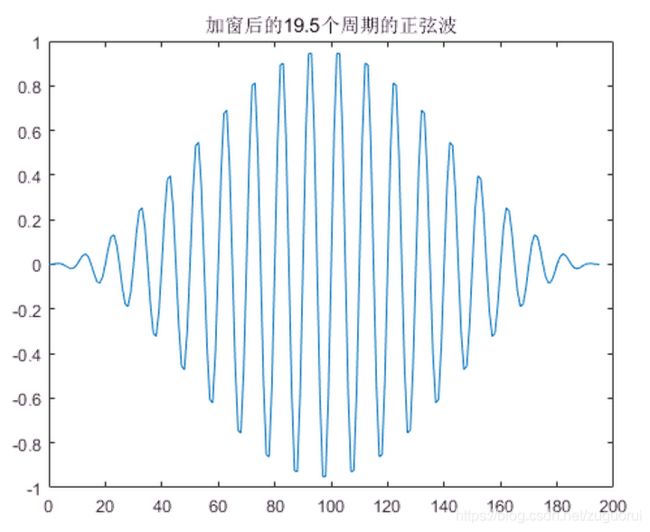
plot(x, sinWave);
title("加窗后的19.5个周期的正弦波");
b = fft(sinWave);
%b = circshift(b', fix(length(sinWave) / 2))';
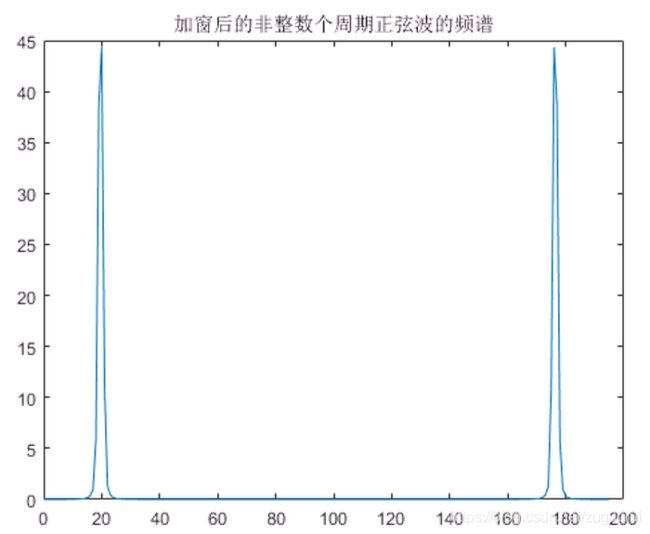
plot(x, abs(b));
title("加窗后的非整数个周期正弦波的频谱")

之后信号就变成这样

其频谱

可以看到，加窗之后，频率泄漏的情况改善了很多。

从另一方面理解。之前的博客《数字信号处理4：采样定理》中证明了一个重要的结论：时域卷积等于频域相乘，时域相乘等于频域卷积。

因此，将信号做傅里叶变换，其实隐含了一个过程，就是原信号的频谱与窗函数的频谱进行卷积。而如果不想改变原信号频谱，最理想的情况就是让它与一个冲激信号进行卷积，这样原信号的频谱其实只是发生了位移。这样一来，我们就希望能有一个窗函数，它的频谱是一个冲激函数，或者尽量接近冲激函数。

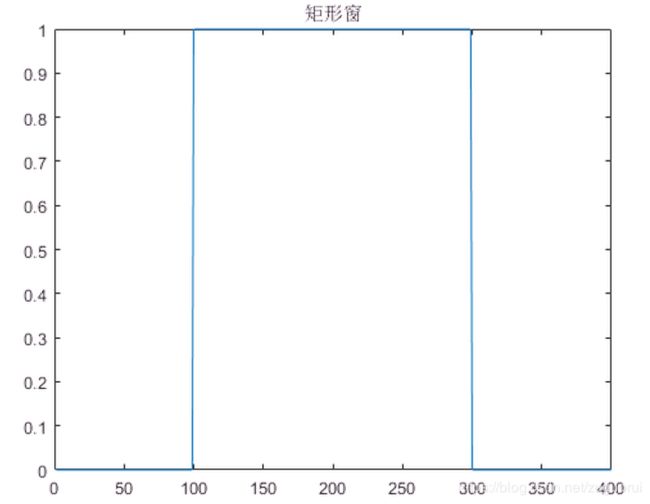
对于一段信号，不加窗等价于加矩形窗。我们不妨看一下矩形窗的频谱：

a=zeros(1, 400);
a(100:299) = ones(1, 200);
b = fft(a);
b = circshift(b', 200)';
plot(a);
title("矩形窗")

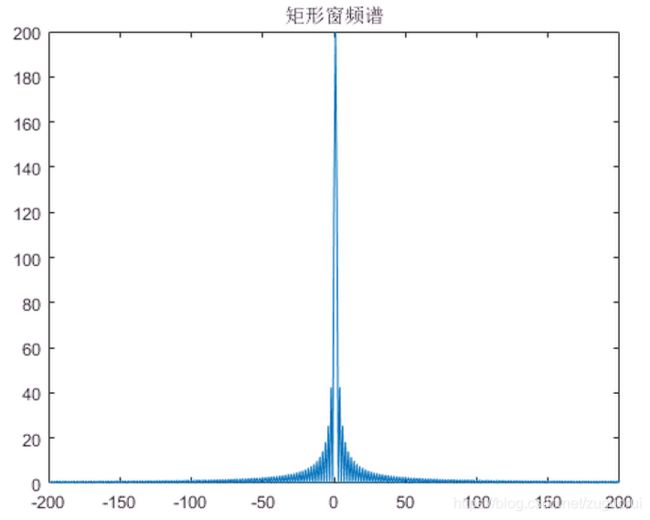
plot([-199:1:200], abs(b));
title("矩形窗频谱")

显然，矩形窗有很多旁瓣，与这样的信号在频域上做卷积，会改变原信号的频谱。

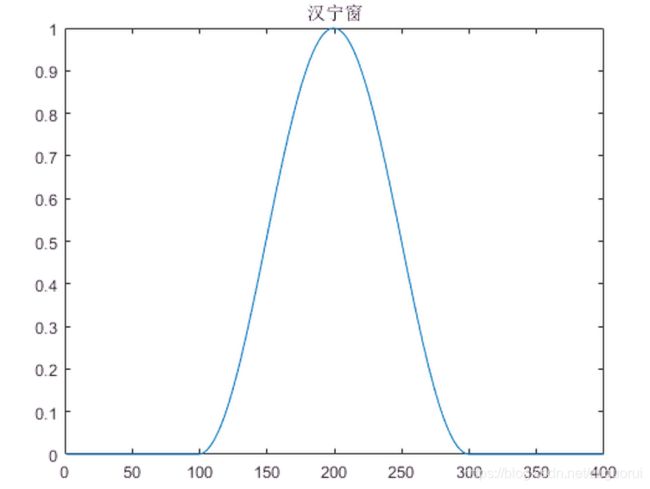
而看一下汉宁窗：

a=zeros(1, 400);
a(100:299) = hanning(200)';

plot(a);
title("汉宁窗")
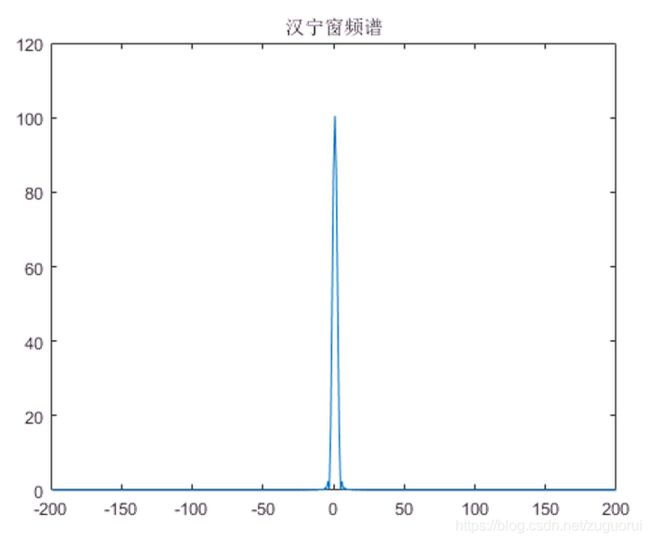
b = fft(a);
b = circshift(b', 200)';

plot([-199:1:200],abs(b));
title("汉宁窗频谱")

可见汉宁窗的频谱相当接近一个冲激函数。

至此，窗函数的意义已经明了：消除傅里叶变换过程中的频率泄漏。

4. FIR滤波器设计

滤波器是一个线性时不变系统，我们使用一个差分方程来表示该系统的信号传输特性：

$$y[n]=-\sum _{k=1}^N{a}_{k}y[n-k]+\sum _{k=0}^{M-1}{b}_{k}x[n-k]$$

如果$a_k\ne 0$，那么当前输出不仅与当前输入有关，还有过去的$M-1$个输入，以及过去的$N$个输出有关。这样的滤波器成为无限冲激响应滤波器（IIR Filter）。如何理解无限这个词，当前输出与过去的输出有关，那么可以预见，第一个输入对后面所有的输出都会有影响。

如果$a_k=0$，那么当前输出仅与当前输入和过去的$M-1$个输入有关。这样的滤波器被成为有限冲激响应滤波器（FIR Filter）。

这两种滤波器各有优缺点，IIR的优点在于计算快，能以较少的阶数达到性能要求。但设计比较复杂，而且难以设计出具有准确频率响应的滤波器，另外，IIR滤波器的相位不可能是线性的。

而FIR滤波器则反了过来，设计简单，能快速设计出具有精确线性相位以及需要的频率响应的滤波器。但是需要较高的阶数才能达到滤波要求。

设$h[n]$是滤波器，$H[k]$是$h[n]$的傅里叶变换。

我们从频域滤波开始，既然从频域调节就可以达到滤波器的目的，那么干脆将频域上调节的系数看做$H[k]$，然后用傅里叶逆变换求出$h[n]$，频域相乘等于时域卷积，使用$h[n]$与信号$x[n]$进行卷积即可。

首先要明确的一个点，为什么滤波器要是线性相位？按照傅里叶变换公式

$$X[k]=|X[k]|e^{-j{a}_k{w}_0}$$

然后有一滤波器$h[n]$，其频谱是

$$H[k]=|H[k]|e^{-j{b}_k{w}_0}$$

当$X[k]$与$H[k]$的每一项相乘。
$$Y[k]=H[k]X[k]=|H[k]||X[k]|e^{-j(a_k+b_k)w_0}$$

我们已经知道傅里叶变换是可逆的。所以对于$X[k]$来说

$$x[n]=\frac{1}{N}\sum _{k=<N>}|X[k]|e^{-j{a}_k{w}_0}{e}^{jk{w}_{0}n}=\frac{1}{N}\sum _{k=<N>}|X[k]|e^{j(kn-a_k)w_0}$$
得出的结果必然是实数。
那么对于$Y[k]$：

$$y[n]=\frac{1}{N}\sum _{k=<N>}|X[k]H[k]|e^{j(kn-a_k-b_k)w_0}$$

假设$|H[k]|=1$，相当于没有对$X[k]$进行调节，此时只看$b_k$。
当$b_k=0$时，就退化成$x[n]$的傅里叶逆变换，这个时候$x[n]$自然是没有问题，但是我们知道对于非全0的$h[n]$来说，$H[k]$不可能是零相位的。
如果$b_k$是个常数，也就是$H[k]$的相位是线性的，很显然，$y[n]$只是相当于将$x[n]$延迟了$b_k$。
而如果相位是非线性的，则无法保证$y[n]$是实数。

接下来的任务就是确定$b_k$的值。

注意，从这里开始，就与大多数教科书讲的不一样了

设
$$H[k]=H_a[k]e^{-j{b}_k{w}_0}$$

其中，$H_a[k]$是其$H[k]$的幅度响应，因此$|H_a[k]|=|H[k]|$。

由傅里叶变换公式可知，对于实序列的傅里叶变换，有
$$H[k]=H^{\ast }[-k]=H^{\ast }[N-1-k]$$

因此，$|H[k]|=|H[-k]|$，意味着$H_a[k]$既可以是偶函数也可以是奇函数。

很多教材将$H_a[k]$是奇函数还是偶函数区分开来，并且由于滤波器长度N可以为奇数或偶数，因此衍生了四种情况，记起来颇为麻烦。

实际上，我们只要考虑$H_a[k]$是偶函数的情况，因为它已经可以构造任何形式的FIR滤波器。而奇函数的形式却无法构造调节低频的滤波器。

第一步：构造幅度响应

这一步是我们根据滤波器要求来构造的。举例来说，信号采样率是16kHz，我们要将4kHz以上的信号降低60dB。

这个时候，根据滤波器长度来区分不同的情况。

如果滤波器长度为20，那么在0点处对应的是0Hz，每两个点频率差为$16000/20=800$Hz。那么第4点对应3200Hz，第5点对应4000Hz，第10点对应的是8000Hz，刚好是采样率为16k能表示的最大信号频率。

要将4kHz以上的信号降低60dB，则第5点到第10点，其幅度响应都为0.001（通过dB换算）。而第0点到第4点，幅度响应都为1。

现在确认了11个点，那剩下的9个点呢？别忘了此时幅度响应是偶函数，而且傅里叶变换后的频谱现在是周期为20的周期函数。因此第11点与第9点相同，一直往后，第19点与第1点相同。

因此得到的幅度响应为

如果滤波器长度为21，那么每两个点频率差为$16000/21\approx 762$Hz。按照同样的方式，可以得到下表：

注意其中3810Hz处将幅度响应设为0.01，因为过于陡峭的变化会导致吉布斯现象出现抖动。其实以上两个响应我没有经过检验， 可能也会存在吉布斯现象。

第二步：构造相位响应
之前已经证明过FIR滤波器必须是线性相位的。但是我们不知道线性系数是多少。这里我们先假设它是1。

使用上面的偶数长度滤波器的幅度响应。不过由于滤波器长度太短，为了防止吉布斯现象，我们降低6dB即可，这样，对应的幅度响应约为0.5。

H_amp = [1, 1, 1, 1, 1, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1, 1, 1, 1];

N = length(H_amp);

w0 = 2 * pi / length(H_amp);

theta = (w0 * 1) .* [0 : 1 : N-1];

H_phase = exp(1i .* theta);

H = H_amp .* H_phase;

h = ifft(H);

plot(real(h));
title("h的实部");

plot(imag(h));
title("h的虚部");

显示如下：

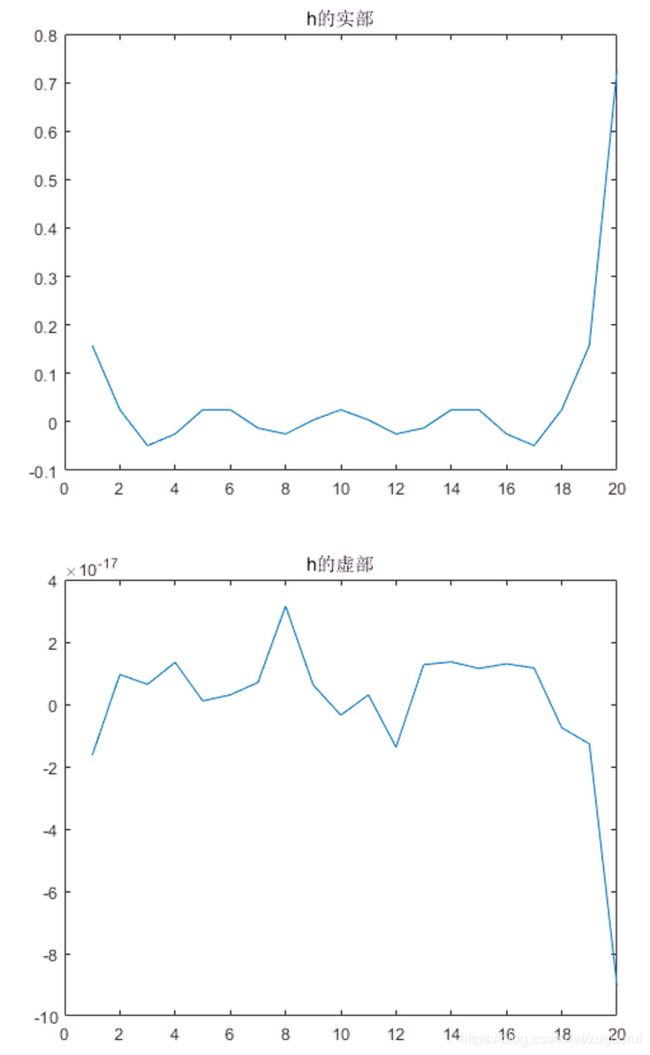
虚部是一些很小的数，这可能是由于计算误差引起的，可以忽略掉。

但是实部是不太对的，因为毕竟之后我们要加窗的，这样一加窗，这个滤波器肯定就变了，我们至少要保证起主要作用的那些值比较大的点在加窗之后要保留下来。因此，我们不妨将其循环移位$N/2$。再来看效果。

修改代码如下，对h进行循环移位，之后加汉宁窗，并且使用freqz函数查看滤波器的频域响应。

H_amp = [1, 1, 1, 1, 1, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1, 1, 1, 1];

N = length(H_amp);

w0 = 2 * pi / length(H_amp);

theta = (w0 * 1) .* [0 : 1 : N-1];

H_phase = exp(1i .* theta);

H = H_amp .* H_phase;

h = ifft(H);

h = circshift(h',fix(N/2))';

plot(real(h));
title("h的实部");

plot(imag(h));
title("h的虚部");

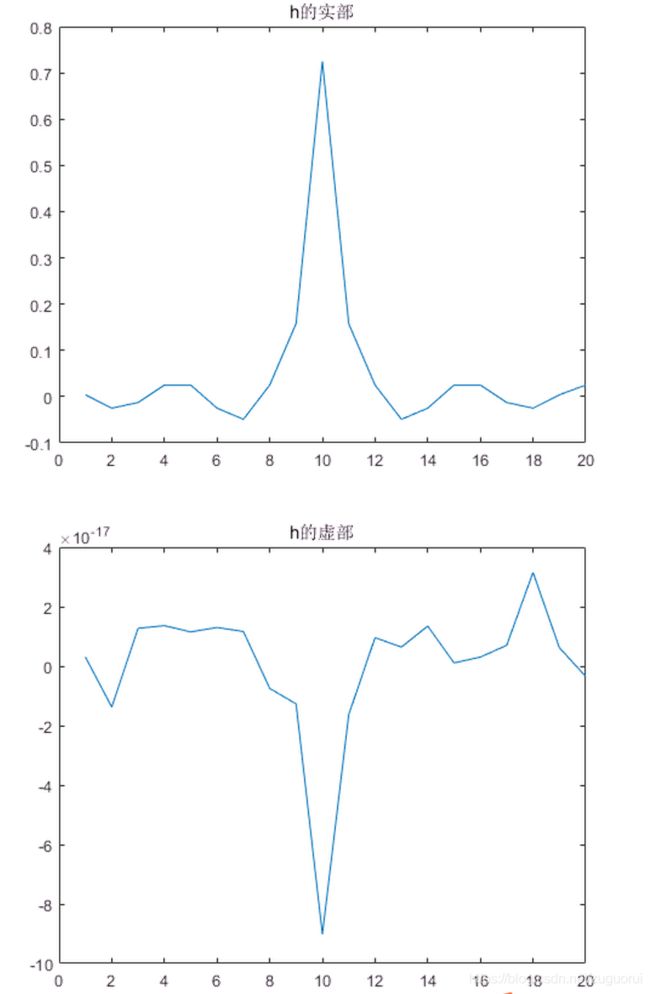
其频域响应为：

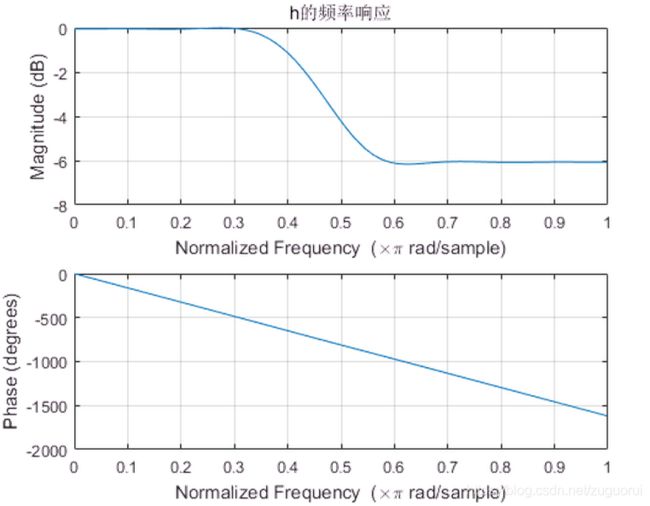
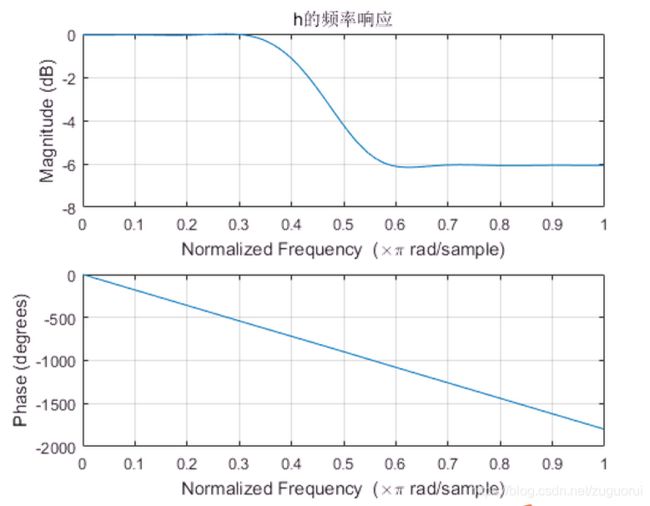
可以看到，非常完美的线性相位，并且滤波器指标也达到我们的要求。

其实对于循环移位这个操作，相当于把h[n]延迟了N/2。由傅里叶变换的位移定理：

$$\sum _{n=<N>}x[n-a]e^{-jk{w}_{0}n}=\sum _{n=<N>}x[n-a]e^{-jk{w}_0(n-a)}{e}^{-jk{w}_{0}a}=X[k]e^{-jk{w}_{0}a}$$
因此，对于FIR滤波器来说，线性相位的系数是N/2。若N为奇数，则为(N-1)/2。线性相位系数必须是正数。
之前我们实际上已经给h[n]延迟了1，因为相位的系数是1。这次我们直接将1改为N/2，并且去掉后面的循环移位操作。

H_amp = [1, 1, 1, 1, 1, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1, 1, 1, 1];

N = length(H_amp);

w0 = 2 * pi / length(H_amp);

theta = (w0 * fix(N/2)) .* [0 : 1 : N-1];

H_phase = exp(1i .* theta);

H = H_amp .* H_phase;

h = ifft(H);

%h = circshift(h',fix(N/2))';


plot(real(h));
title("h的实部");

plot(imag(h));
title("h的虚部");

window = hanning(N);

h = h .* window';

freqz(real(h));
title("h的频率响应");

最终的频率响应是

5. 总结

好了，至此FIR滤波器的构造方式已经讲完了，实际上关于滤波器指标还有很多细节的东西需要学习，比如滤波器长度、截止频率等。

总结一下构造FIR滤波器的步骤：

1. 根据要求构造幅度响应。
2. 构造相位响应，必须是线性相位，线性系数为：N为偶数时是N/2；N为奇数时是(N-1)/2。
3. 幅度响应和相位响应合起来成为滤波器频谱$H[k]$。
4. 将$H[k]$进行傅里叶逆变换并取其实部得到滤波器$h[n]$。
5. 对$h[n]$加窗。

具体的matlab代码可以查看我的github：FIR-filter。博客中使用的示例代码都可以从中找到。包含了一个我已经写好的fir_filter.m用来直接生成FIR滤波器。