惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模
所有程序代码和数据已经上传至Github:
https://github.com/yzmj0986/VariableStep-AllanVariance.git
基于步长可变序列的快速Allan方差算法见文章:Noise Identification and Analysis in MEMS Sensors Using an Optimized Variable Step Allan variance.
目录导航:
- 应用背景:
- Allan方差的计算原理:
- 传感器随机误差建模
- 程序代码:
- 改进思路
应用背景:
根据误差特性将传感器误差分为确定性误差和随机性误差,确定性误差,例如未对准误差和比例因子不稳定,可以通过转台或者温度试验进行提前标定,并在传感器内部进行修正。随机误差是指在输出信号中混合的附加随机噪声,通常包括量化噪声,角度随机游走,偏置不稳定性,速率随机游走和速率斜坡,可以通过在线补偿消除。与功率谱密度(PSD)和自回归移动平均(ARMA)模型相比,Allan方差是识别和分析噪声的最简单的时域方法,从1998年起IEEE建议使用AV方法来确定光学陀螺仪和MEMS惯性传感器的误差。
Allan方差的计算原理:
Allan方差的计算基于整群抽样技术。假设以采样间隔![]() 采集MEMS传感器的信号,首先将N个采样数据分成K簇,每个簇包括m个采样数据,簇长度为m的时间表示为
采集MEMS传感器的信号,首先将N个采样数据分成K簇,每个簇包括m个采样数据,簇长度为m的时间表示为![]() 。那么典型的Allan方差可以基于均方误差表示为:
。那么典型的Allan方差可以基于均方误差表示为:
其中<·>表示求平均操作,通过平均归一化频率偏差![]() 来计算
来计算![]() :
:
但其实大多数信号都是在相位和频率偏差的离散值(也就是离散信号),假设θ是相位偏差,平均频率偏差![]() 可以定义为:
可以定义为:
因此,离散时间信号的Allan方差可以改写为:
其中,![]() 是离散采样时间,
是离散采样时间, ![]() 是n时刻时的相位偏差,且
是n时刻时的相位偏差,且![]() 。离散时间采样间隔为
。离散时间采样间隔为![]() 。
。
传感器随机误差建模
下图为MEMS传感器中的主要误差分类。对于零偏、刻度因子误差等静态误差,可通过卡尔曼滤波、递归最小二乘等方法实现在线补偿。但在线滤波器无法对具有随机特性的噪声进行有效估计,因此应使用Allan方差进行各项随机误差辨识,并通过拟合求出各项噪声的系数,实现对随机误差的建模过程。由于Allan方差是MEMS传感器噪声稳定性的表征,因此Allan方差与随机过程PSD的积分关系为:
通过替换上式的积分计算可以导出Allan方差作为典型随机误差的时间函数,通过 ![]() 和
和![]() 的对数图,能够清楚表征MEMS传感器中的随机误差,如下图所示。其中
的对数图,能够清楚表征MEMS传感器中的随机误差,如下图所示。其中![]() 是Allan方差的平方根,也称为Allan标准偏差。
是Allan方差的平方根,也称为Allan标准偏差。
根据每种噪声的Allan方差及其斜率系数,假设各种误差来源统计独立,总的Allan方差可以表示为各误差的和:
程序代码:
%Allan Variance的原始实现,并设置了可变的步长d,实现对求取时间的控制。
%**********author:zytjasper 2018/12/10.************%
%Reference:Noise Identification and Analysis in MEMS Sensors Using an Optimized Variable Step Allan variance
clc;
clear all;
tic;
data = xlsread('data.xlsx');
X = data(1:720000,1)*3600; %读取数据,以陀螺仪某一轴为例
Ts = 0.01; %采样时间
[N,M] = size(X);
N_max = floor(N/3);%(N/3)
T = zeros(N_max,10);
R = zeros(N_max,10);
for d = 1 %设置迭代的步长为d,当d=1时为传统的Allan方差
Allan = zeros(N_max,2);
Cluster_mean = zeros(N,1);
for n = 1:d:N_max %每一簇的簇长
K = floor(N/n);
for k = 1:K
Cluster_mean(k,1) = mean(X((n*(k-1)+1):(n*k),1));
end
Cluster_diff = diff(Cluster_mean(1:K),1);
Allan(n,1) = n*Ts; %Time tau
Allan(n,2) = sum((Cluster_diff.^2))/(2*(K-1));
end
Allan(any(Allan,2)==0,:)=[]
TUP = ceil(N_max/d);
RUP = ceil(N_max/d);
T(1:TUP,d)=Allan(:,1);
R(1:RUP,d)=Allan(:,2);
end
x1 = T(:,1);
y1 = R(:,1);
a= [1 2 3 4 5];%函数拟合过程
a(1:5)=lsqcurvefit(@test,a,x1,y1);
f=a(1)*x1.^(-2)+a(2)*x1.^(-1)+a(3)*x1.^(0)+a(4)*x1.^(1)+a(5)*x1.^(2);
figure(1)=figure('color',[1 1 1]);
loglog(T(:,1),R(:,1),'color',[255/255,215/255,0/255]);
hold on;
loglog(x1, f,'r','LineWidth',1.3);
hold on;
xlabel('Cluster Time (sec)');
ylabel('Allan Deviation (deg/h)');
grid on;
legend(' Step size=1',' Step size=2',' Step size=3',' Fitting Curve')
toc; test拟合程序:
function f=test(a,x)
f=a(1)*x.^(-2)+a(2)*x.^(-1)+a(3)*x.^(0)+a(4)*x.^(1)+a(5)*x.^(2);
end运行结果:(别介意标注,红线应该是拟合曲线)
运行时间会在1K-1.2K秒左右,这是正常范围,Allan方差的迭代原理就是很慢很慢很慢,我在Reference中做了加速的优化,终稿刊号出来了我就会附上原文的。【2019.11.20更新,文章已经贴出,改变步长后的Allan方差速度有大幅度的提升】
改进思路
给采样序列m中加入可变步长(等比等差都可以,文中用的是等差),即:
![]()
步长可变的Allan方差算法原理示意图如下:
分别将步长![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第8张图片](http://img.e-com-net.com/image/info8/4600248fb9234db0a3a79e282ec88c8d.jpg) 设置为1,5,10,15,20,25,30,35,40,并将误差拟合曲线叠加可得到下面的误差辨识结果:
设置为1,5,10,15,20,25,30,35,40,并将误差拟合曲线叠加可得到下面的误差辨识结果:
该方法显著的减少了误差建模的计算量,在确保误差估计精度的同时实现了对传感器时变稳定性的快速跟踪。此外该步长可变序列的思路还可以应用在DAVAR方法中,具体过程见论文。
只是一篇普通的EI论文,不足之处欢迎各位学习与指正。
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第1张图片](http://img.e-com-net.com/image/info8/f10c5b04bdb248d0a2fa821220a31194.jpg)
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第2张图片](http://img.e-com-net.com/image/info8/31aede27787346369095b5fd5f4a51e6.jpg)
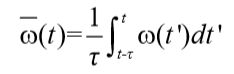
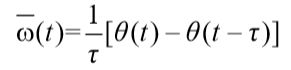
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第3张图片](http://img.e-com-net.com/image/info8/4988ec460b6a4d60b6b3950959762b98.jpg)
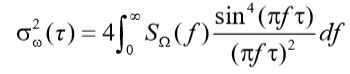
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第4张图片](http://img.e-com-net.com/image/info8/fdb14927aa294beb86262a7645c1ef7f.jpg)
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第5张图片](http://img.e-com-net.com/image/info8/467eca695dbf496ab15f938a65cdcf2b.jpg)
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第6张图片](http://img.e-com-net.com/image/info8/87e2988bdc3942a3965d73323a83a1fe.jpg)
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第7张图片](http://img.e-com-net.com/image/info8/d644ea4ec2d644bb872d94bebd0fd749.jpg)
![惯性组合导航原理—[4] 步长可变的快速Allan Variance:传感器随机误差建模_第9张图片](http://img.e-com-net.com/image/info8/1e5ce64bf4514b268e795eeedccce9c6.jpg)