最短路四大算法证明以及分析（Flord Bijkstra Bellman-ford SPFA）

此博文不具体给出其算法的代码，只对其中算法进行分并且给予证明

PS：这些算法我不用证明都是它是正确的（上世纪的数学家看着这些都不用证明，为啥，很简单的），但是我坚持重新证明一遍实际是为了加深印象，并且理解其中的道理和思想，这样在以后的运用中才能灵活运用，当然证明这些算法也

 

算法一：Flord 算法，也是传说中的只用五行就可以解决的多源最短路径问题

采用邻接矩阵来储存图，时间复杂度为O（n^3），能解决含正权，负权的最短路径，不能解决含有负环的最短路径（负环也没有最短路径）

 

for(k=1;k<=n;k++)
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            if(e[i][j]>e[i][k]+e[k][j])
                 e[i][j]=e[i][k]+e[k][j];

 

 

 

当k=1时进行一个嵌套的for循环求出来的是任意两点之间只允许经过点1的最短路径，这个都可以理解吧。

(￣▽￣)"

当k=2时，经过一个if else的判断最终求出来的是任意两个顶点之间只允许经过1 2号顶点的最短路径。

这时候可能有人说在进行 if      else 之后判断的是i->j通过2号顶点路径后路径能否缩小，那么如果i->j还能通过1号顶点再次缩小路径，那还能体现出来吗？

好的下面咱们来证明

假设咱们判断过之后i->j之间通过2号顶点可以缩小路径，此时i与j的路径为i->2->j，假设还可以通过1号顶点缩小路径（也就是上面所说的情况）

此时1号顶点肯定在i->j之间，也就是i->2或2->j之间 ，而咱们在第一次for循环之后的意义上面已经说过了，即任意两点可以经过1号顶点后更新的最短路径，那么回过来即i->2之间或者2->j之间若可以经过1号顶点在缩短路径，那么铁定在第一次循环后就已经在i->2或2->j之间添加1号顶点了，所以上面的担心是多余的(●'◡'●)

当k=2的循环结束后，得到的意义便是任意两个顶点只允许经过1 2号顶点的最短路径

 

当k=n时  循环结束后便是任意两点之间允许经过1~n个顶点后的最短路径，（如果有疑问，那么再按着刚刚在2号顶点的证明过程比较一下）

 

 

算法二：dijkstra算法 （求单源最短路径，只允许正权）

这个是比较常用的算法，其常用的储存图的方式有邻接矩阵，邻接表两种。采用邻接矩阵的时间复杂度为O（n^2）

在此用邻接矩阵来举例子

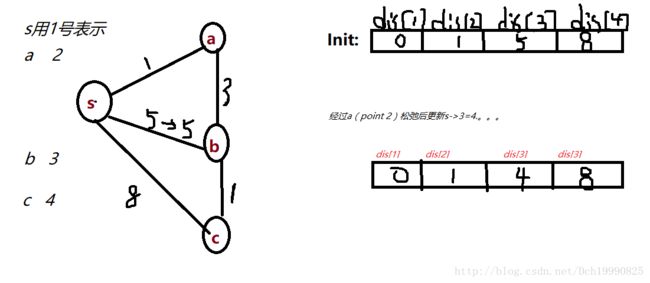
先说一下算法原理，初始化就不说了吧（任意两点之间之间路径为INF，自己与自己的路径为0）随后输入图。

用一个dis[]数组记录源点到其他点的直接路径。假设源点号为S，并且用数组book[]来表示s->其他点的最短路径是否确定，确定的点令其值为1（book[s]=1）。

然后从dis[]数组找s->v最小的值，假设为这个顶点为u，那么s->u的最短路径肯定就确定了。为啥 ？因为s->u若再经过其他点所成的路径一定比s->u的路径的大。

已经确定s->u是最短路径后，松弛u点到其他点的路径,令book[u]=1。（这点是关键）

所以算法分三个步骤

1.然后再从dis[]从最短路径未确定的路径找出的最小值，令其为确定的最短路径（假设这个顶点是u），令book[u]=1;（证明下面在说）

2.从u点松弛

3.重复以上1. 2点直至所有点的最短路径确定。

 

 

也许有很多人对第1步有些不解。为什么从中找出的符合条件的u的最短路径一定确定了呢？别急下面来证明

看这个图

第一次  找出s->a最小，那么令此时s->a的路径为最短路径，令book[2]=1，（这个都没疑问吧）...... 然后松弛a->b得到mid=dis[a]+map[a][b]b的路径变小了

第二次，再次按步骤1找出最小的为dis[b]，此时的dis[b]为s->b的最短路径。为啥？假设此时dis[b]的值不是s->b的最短路径，那么要想找s->b的更小路径至少中转至一个顶点v，且s->v的距离满足dis[v]b的路径一定>=dis[b]，

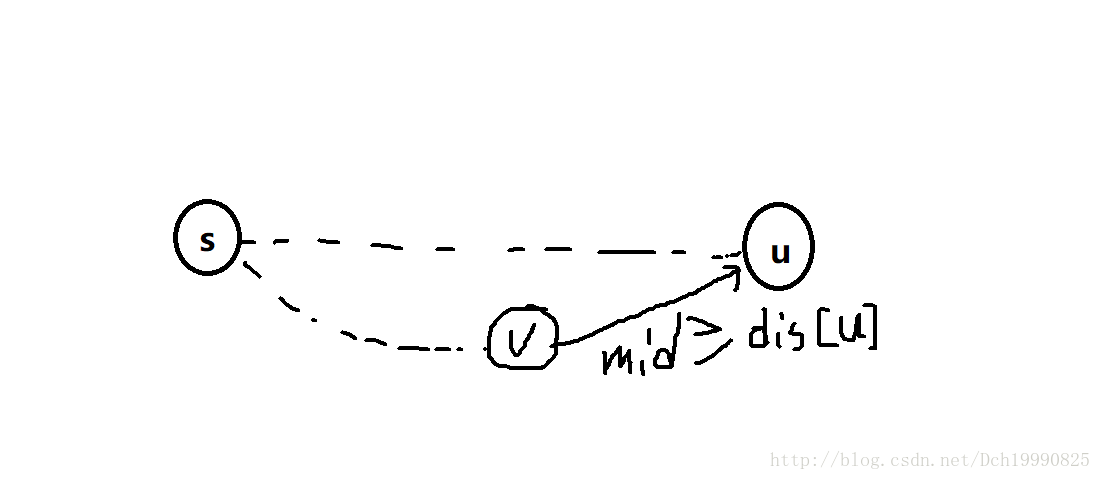
也就是下面这个原理

u为此时经过步骤1确定的点，假设s->u的距离不是最短路径，即存在另一条路径s->v->u（你也可以假设s->v之间还有许多点，但是我们要确保v->u是直接的，即不经过任何一个中转点）使得路径长度mid

又因为假设的路径中v是在s->u之间，所以v的最短路径已经确定且v经过松弛，即v到任何点的都经过松弛（包括点u），所以此时我们找的mid是一定>=dis[u]的，即假设不成立。               

所以你就默认他们是最短路径这一事实吧(￣▽￣)"

代码：

附上dijkstr算法

 

/*
dijkstr 算法
二步：
1.初始化
2.每次找出dis最小值则为确定对短路
注意：minn=INF 或者找到答案这一提前跳出
*/
#include
#include
#include
#include
#include
#include
#include
#define N 1010
#define INF 0x3f3f3f3f
#define MOD 1000000007
#define WC 1e-6
typedef long long LL;
using namespace std;
int book[N],dis[N],map[N][N];
void dijkstr(int n)
{
    int t=n,minn,u,to;
    memset(book,0,sizeof(book));
    for(int i=1;i<=n;i++)
        dis[i]=INF;
    dis[1]=0;
    while(t--)
    {
        minn=INF;
        for(int i=1;i<=n;i++)
        {
            if(!book[i]&&dis[i]

 

 

 

 

 

 

 

 

有时间再补充另两个算法的证明

 

附上SPFA代码

/*
SPFA
三步
1.初始信息 将初始点加入队列
2.每次从队列的第一个点进行松弛，可以更新另一个点则将其加入队列（已经加入队列则不需要再次加入）
2.队列为空结束
*/

#include
#include
#include
#include
#include
#include
#include
#include
#define N 1010
#define INF 0x3f3f3f3f
#define WC 1e-6
typedef long long LL;
using namespace std;
int book[N],dis[N],map[N][N];//存信息
queuemmp;
void SPFA(int n)//n得出范围  输入map就OK
{
    int to;
    memset(book,0,sizeof(book));
    for(int i=1;i<=n;i++)
        dis[i]=INF;
    dis[1]=0;
    while(!mmp.empty())
        mmp.pop();
    mmp.push(1);
    while(!mmp.empty())
    {
        int u=mmp.front();//出队伍
        mmp.pop();
        book[u]=0;
        for(int i=1;i<=n;i++)//松弛
        {
            to=dis[u]+map[u][i];
            if(to

 

 

 

附上bellman算法

/*
bellman算法   可以判断负环
1.初始化dis （struct）edge
2.遍历所有边
2.更新成功则进行下一次
*/
#include
#include
#include
#include
#include
#include
#include
#define N 4010
#define INF 0x3f3f3f3f
#define WC 1e-6
typedef long long LL;
using namespace std;
int dis[N];
struct node{
int u,v,w;
}e[N];
void bellman(int n,int cnt)
{
    int to,t,flag;
    for(int i=2;i<=n;i++)
        dis[i]=INF;
    dis[1]=0;
    t=n-1;
    while(t--)
    {
        flag=0;
        for(int i=0;i