ELRCN（富集长期递归卷积网络）微表情识别

Enriched Long-term Recurrent Convolutional Network for Facial Micro-Expression Recognition

论文地址：https://arxiv.org/abs/1805.08417
源码地址：https://github.com/IcedDoggie/Micro-Expression-with-Deep-Learning

网络架构

ELRCN的总体框架分为两个主要模块：首先通过CNN模块提取深度空间特征，将每个微表情帧编码成特征向量，然后通过将特征向量通过一个长短时记忆（LSTM）模块，在时域上学习。

该框架包含两种不同的网络变体：

1. Spatial Dimension Enrichment (SE)通过输入通道叠加来丰富空间维度
2. Temporal Dimension Enrichment (TE)通过深度特征叠加来丰富时间维度

该方法能够实现合理的良好性能，而不需要数据增强。

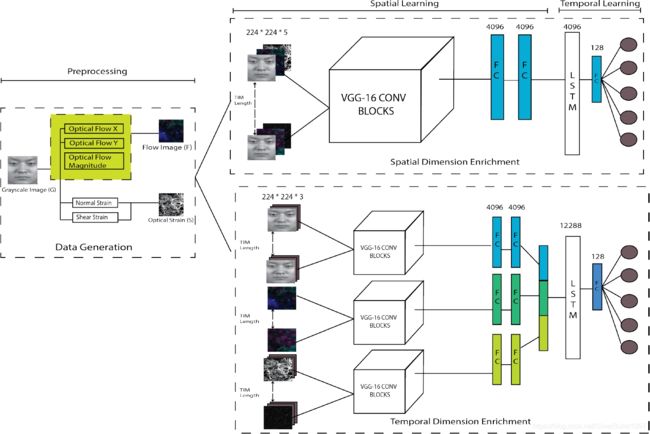
图1：ELRCN的总体架构

架构参考文献：Donahue J, Anne Hendricks L, Guadarrama S, et al. Long-term recurrent convolutional networks for visual recognition and description[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 2625-2634.

预处理

使用TV-L1方法计算光流(optical flow)

TV-L1方法：Zach C, Pock T, Bischof H. A duality based approach for realtime TV-L 1 optical flow[C]//Joint pattern recognition symposium. Springer, Berlin, Heidelberg, 2007: 214-223.

优点：噪声鲁棒性好，防止流动不连续性

光流的水平和垂直分量定义如下：
$$v={\left[p=\frac{dx}{dt},q=\frac{dy}{dt}\right]}^T$$
$dx$和$dy$分别表示沿$x$和$y$维度的像素变化估计，$dt$表示时间变化。

通过连接水平/垂直光流图像$\mathbf{p},\mathbf{q}$和光流幅度$\mathbf{m}=|v|$，得到三维光流图像。

通过计算光流的导数获得光学应变(optical strain)

光学应变能够正确表征两个连续帧之间存在的可变形物体的微小移动量， 由位移矢量$\mathbf{u}=[u,v{]}^T$描述

有限应变张量定义为：
$$ϵ=\left[\begin{array}{cc}{ϵ}_{xx}=\frac{\delta u}{\delta x}& {ϵ}_{xy}=\frac{1}{2}\left(\frac{\delta u}{\delta y}+\frac{\delta v}{\delta x}\right)\\ {ϵ}_{yx}=\frac{1}{2}\left(\frac{\delta v}{\delta x}+\frac{\delta u}{\delta y}\right)& {ϵ}_{yy}=\frac{\delta v}{\delta y}\end{array}\right]$$
$\left({ϵ}_{xx},{ϵ}_{yy}\right)$为法向应变分量，沿$x$和$y$方向的变化；$\left({ϵ}_{xy},{ϵ}_{yx}\right)$为切向应变分量，由两个轴的形变引起角度变化。

每个像素的光学应变大小可以使用法向和切向应变分量的平方和来计算：
$$|ϵ|=\sqrt{{ϵ}_{xx}^2+{ϵ}_{yy}^2+{ϵ}_{xy}^2+{ϵ}_{yx}^2}$$

空间域学习

空间维度富集(SE)

SE模型通过沿输入通道堆叠光流图像($F\in {\mathbb{R}}^3$)，光学应变图像($S\in {\mathbb{R}}^2$)和灰度原始图像($R\in {\mathbb{R}}^2$)，使用更大的输入数据维度进行空间学习，表示为$x_t=\left(F_t,S_t,G_t\right)$。 因此，输入数据为224 * 224 * 5，这就需要从头开始训练VGG16模型。 最后的FC层将输入数据编码成固定长度为4096的矢量$ \phi\left(x_{t}\right) $。

时间维度富集(SE)

TE模型利用VGG-Face模型的预训练权重进行迁移学习， 为满足VGG-Faces模型所需的224 * 224 * 3的输入尺寸，复制S和G图像(${\mathbb{R}}^2\to {\mathbb{R}}^3$)。在训练阶段对每个输入数据在单独的VGG-16模型中进行微调，每个模型在最后的全连接层产生一个长度为4096的特征向量$\varphi \left(x_t\right)$ ，最终长度为12288的特征向量被传递到循环网络中。

时间域学习

通过LSTM网络学习空间编码的输入序列$\varphi \left(x_t\right)$ ，将$h_{t-1}$时刻的输入$\varphi \left(x_t\right)$ 映射到$h_t$时刻的输出$z_t$并更新隐藏状态$h_t$，LSTM层顺序堆叠并连接到FC层将$z_t$编码到低维，$\hat{y}=W_z{z}_t+b_z$，预测值可表示为：
$$P\left(y_t=c\right)=\mathrm{softmax}\left({\hat{y}}_t\right)=\frac{\exp \left({\hat{y}}_t,c\right)}{{\sum }_{c^{\prime }\in C}\exp \left({\hat{y}}_t,c^{\prime }\right)}$$
其中$C$是结果的离散有限集，$y_t\in C$。

通用网络配置

网络训练使用自适应时期或早期停止，最大设置为100个时期。 基本上，当损失评分停止改善时，每次折叠的训练将停止。使用自适应矩估计(Adam)作为优化器，学习率为$10^{-5}$，衰减为$10^{-6}$。对于时间域学习，LSTM层之后的FC层的数量固定为1。

评估

数据集与预处理

本文采用CASME-II和SAMM数据集进行实验，均裁剪并缩放得到224 * 224的面部图像，应用长度为10的时域插值模型(TIM)将样本序列拟合到期望固定时间长度的递归模型中。

Single Domain Experiment 单数据集实验

本文在CASME-II数据集上进行单数据集实验。

表1：本文提出的方法与其他微表情识别方法的比较

由表1可见，本文所提出的ELRCN方法超过了LBP-TOP的基线结果，且TE变体明显优于SE变体，这表明了为每种类型的数据单独微调网络的重要性。

Cross Domain Experiment 跨数据集实验

本文的跨数据集实验采用两个跨数据集协议——Micro-Expression Grand Challenge (MEGC) 2018提供的Composite Database Evaluation (CDE)和Holdout Database Evaluation (HDE)，CDE包含CASME-II和SAMM数据集中的样本，剔除第6和第7个目标类别后共计47个被试，并遵循LOSO协议；HDE从相对的数据集中采集训练和测试集（即在CASME II上训练，在SAMM上测试，反之亦然），然后将每一折的结果取平均即为总体结果。

Composite Database Evaluation (CDE)

表2：CDE协议的评估结果

表2展示了CDE协议的评估结果，SE模型表现出了比TE模型更强的结果(WAR 0.57)，这与CASME-II的单数据集实验结果相反。

图2：CDE协议下ELRCN-SE的混淆矩阵

图2提供了CDE协议下ELRCN-SE的混淆矩阵，由于训练样本数量较大，I类和III类的结果最好

Holdout Database Evaluation (HDE)

表3：HDE协议的评估结果

表3展示了HDE协议的评估结果，SE模型超过了TE模型和基线结果。

图3：HDE协议下ELRCN-SE的混淆矩阵，在CASME-II上训练，SAMM上测试

图4：HDE协议下ELRCN-SE的混淆矩阵，在SAMM上训练，CASME-II上测试

图3和图4提供了HDE协议下ELRCN-SE两种验证方式的混淆矩阵。CASME-II——SAMM折叠（F1 0.409，UAR 0.485，WAR 0.382） 比SAMM——CASME-II折叠得到了更好的效果（F1 0.274，UAR 0.384，WAR 0.322）。CASME-II的第III类训练样本最多，表现最好；同样，训练样本相对不足的类（CASME II中的II类，SAMM中的IV和V类）表现非常差。 因此，小样本量可能仍然是深度学习方法的绊脚石。