剑指offer|解析和答案(C++/Python) (六)

剑指offer|解析和答案(C++/Python) (六)

参考剑指offer(第二版)，这里做一个学习汇总，包括解析及代码。代码均在牛客网进行验证(摘自自己的牛客网笔记)。

整个剑指offer解析链接:
剑指offer|解析和答案(C++/Python) (一).
剑指offer|解析和答案(C++/Python) (二).
剑指offer|解析和答案(C++/Python) (三).
剑指offer|解析和答案(C++/Python) (四).
剑指offer|解析和答案(C++/Python) (五)上.
剑指offer|解析和答案(C++/Python) (五)下.
剑指offer|解析和答案(C++/Python) (六).

习题

两个面试案例
1.把字符串转换成数组
（牛客网上部分题是剑指offer的思考题，不多，下面就是那些剩下的题）
2.变态跳台阶
3.矩形覆盖

1.把字符串转换成数组

将一个字符串转换成一个整数，要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0
输入描述：
输入一个字符串,包括数字字母符号,可以为空
输出描述：
示例1
输入：
+2147483647
1a33
输出：
2147483647
0

思路：
这题本身不难，不够需要注意许多细节。
特殊用例的测试：
1.空指针
2.空字符串""
3.正负号
4.溢出

这里着重讲一下正负数溢出。
参考：
https://zhidao.baidu.com/question/194668811.html
https://zhidao.baidu.com/question/2052829228594311827.html

• A.负数溢出

这里对应的测数数据为"-2147483649"，正确的输出为：0，但很有可能造成错误输出：2147483647。这因为32位的int数据范围是 -2147483648 —— 2147483647。
-2147483649 可以看成 -2147483648 + (-1) 。（补充：计算机中数字全部是以补码的形式进行存储）。
-2147483648的原码是：0x80000000，反码是0xFFFFFFFF，补码是0x80000000。
举例理解：-8的补码。
（1）如果用4位二进制数表示的话，原码1000（“1”表示“-”号，“000”可以看成数字位“111”+1的结果）——反码1111——补码1000。
（2）如果用8位二进制数表示的话，原码1000 1000——反码1111 0111——补码1111 1000。
这也是为什么**-2147483648**补码是0x80000000而不是0x180000000的原因，数字被限定用32位int型数据表示。
-1的原码是0x80000001，反码是0xFFFFFFFE，补码是0xFFFFFFFF。
所以$-2147483649=-2147483648+(-1)$为 0x80000000 + 0xFFFFFFFF =0x7FFFFFFF(补码相加)，而0x7FFFFFFF又等于2147483647，这就是负数溢出，造成错误的原因。
如何判断负数溢出：首先判断负数标志位，接着判断最高位是否为0(因为产生了进位)。

B.正数溢出
正数溢出和负数溢出类似，正数的最大值为2147483647，输入测试数据2147483648，正确的输出为0，但很容易造成错误输出：-2147483648。
一样的分析，2147483648 = 2147483647 + 1。
2147483647 原码=反码=补码=0x7FFFFFFF，1的原码=反码=补码=0x00000001。
2147483647 + 1为0x7FFFFFFF + 0x00000001 = 0x80000000，而0x80000000是**-2147483648**的补码，这就是造成错误的原因。
如何判断正数溢出：首先判断正数标志位，接着判断最高位是否为1(因为产生了进位)。
代码：
C++

class Solution {
public:
	enum Status{kValid = 0, kInvalid};
	int g_nStatus = kValid;
    int StrToInt(string str) {
        g_nStatus = kInvalid;
		long long num = 0;
		//str.size() 获取str长度 不包括\0
		if(str.size() > 0){
			bool minus = false;//负数的标志
			if(str[0] == '+'){
				str = str.substr(1);//截断字符串
			}else if(str[0] == '-'){
				str = str.substr(1);//截断字符串
				minus = true;
			}
			if(str.size() > 0 && str[0] != '\0'){
				num = StrToIntCore(str, minus);
			}
		}
		return (int)num;
    }
	int StrToIntCore(string str, bool minus){
		int num = 0;
		int length = str.size();
		for(int i = 0; i < length; ++i){
			if(str[i] <= '9' && str[i] >= '0'){//合法的输入
				int flag = minus? -1:1;//正负数
				cout<<"str[i]:"<<str[i]<<endl;
				num = num*10 + flag*(str[i] - '0');
				cout<<"num:"<<num<<endl;
				if((!minus&&((num>>31)&0x1) == 1)||//正数溢出
				(minus&&((num>>31)&0x1) == 0)){//负数溢出
				    cout<<"error"<<endl;
					num = 0;
					break;
				}
			}else{//非法输入
				num = 0;
				break;
			}
		}
		return num;
	}
};

Python

# -*- coding:utf-8 -*-
class Solution:
    def StrToInt(self, s):
        # write code here
        length = len(s)
        num = 0
        if length > 0:
            minus = False
            if s[0] == '+':
                s = s[1:]#截断
            elif s[0] == '-':
                minus = True#负数
                s = s[1:]
            if len(s) > 0:
                num = self.StrToIntCore(s, minus)
        
        return num
    
    def StrToIntCore(self, s, minus):
        length = len(s)
        num = 0
        for i in range(length):
            if s[i] >= '0' and s[i] <= '9':
                if minus == True:
                    flag = -1
                else:
                    flag = 1
                num = num*10 + flag*(int)(s[i])
                #判断是否溢出
                if (minus == False and ((num>>31)&0x1) == 1) or \
                    (minus == True and ((num>>31)&0x1) == 0):
                    num = 0
                    break
            else:
                num = 0
                break
        
        return num

2.变态跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

思路：
1.递归求解。分析递归条件，我们用$f(i)$表示青蛙跳i层台阶存在的跳法。
可以得出条件：
$f(1)=1$
$f(2)=2$
$f(i)=f(i-1)+f(i-2)+\dots +f(2)+f(1)+1$
2.循环：自底向上。根据递归公式得到递推公式：
$f(i)=f(i-1)+f(i-2)+\dots +f(2)+f(1)+1$
$f(i-1)=f(i-2)+\dots +f(2)+f(1)+1$
$f(i)-f(i-1)=f(i-1)$
$f(i)=2\times f(i-1)$
$f(i)=2^{i-1}$
于是可以使用循环操作，效率更高。
代码：
C++

class Solution {
public:
    int jumpFloorII(int number) {
		int jumpFloor = 1;
		for(int i = 0; i < number - 1; ++i)
			jumpFloor *= 2;
		return jumpFloor;
    }
};

Python

# -*- coding:utf-8 -*-
class Solution:
    def jumpFloorII(self, number):
        # write code here
        jumpFloor = 1
        for i in range(1, number):
            jumpFloor *= 2
        return jumpFloor

3.矩形覆盖

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

思路：
把2n有多少中覆盖方法记为$f(n)$。用第一个21的小矩形去覆盖大矩形的最左边时有两种选择：竖着放或横着放。
当竖着放的时候，右边还剩下2*(n - 1)的区域，这种情形下，覆盖种类有$f(n-1)$。
当横着放的时候，右边还剩下2*(n - 2)的区域，这种情形下，覆盖种类有$f(n-2)$。
此时$f(n)=f(n-1)+f(n-2)$。其实就是斐波拉契数列。
参考图示：

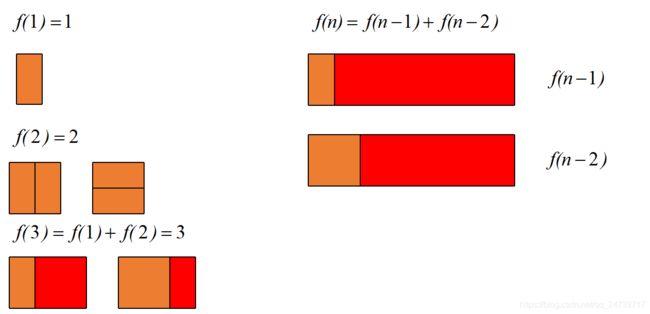
代码：
C++

class Solution {
public:
    int rectCover(int number) {
		if(number < 3)
			return number;
		int rectOne = 2;
		int rectTwo = 1;
		int rectNums;
		for(int i = 3; i <= number; ++i){
			rectNums = rectOne + rectTwo;
			rectTwo = rectOne;
			rectOne = rectNums;
		}
		return rectNums;
    }
};

Python

# -*- coding:utf-8 -*-
class Solution:
    def rectCover(self, number):
        # write code here
        if number < 3:
            return number
        rectOne = 2
        rectTwo = 1
        for i in range(3, number + 1):
            rectNums = rectOne + rectTwo
            rectTwo = rectOne
            rectOne = rectNums
            
        return rectNums