cs231 学习笔记（一）

First Classifier: Nearest Neighbor

训练过程就是记录所有的数据点，在预测阶段对每一条记录（一个图像）与原有数据集进行比较，得出与之最相近的一条记录，其label就是最后的预测值。通常使用的 Distance Metric 来比较图像：

L1依赖于坐标系，当坐标轴转动时L1值随之改变，而L2不会。

KNN

选择K个最近的邻居，随着K的值越大，你的决策边界也会越来越光滑，降噪提高robust

Cross Validation 在数据集比较小时非常有用，但是在deep learning 里不太适用，因为deep learning 通常需要很大的算力，使用交叉验证会使training的代价过于高昂。

使用KNN可以用于不同类型的数据集，使用起来非常的简单，需要考虑不同K的值以及使用那种类型的距离方程（超参数）

Linear Classifier

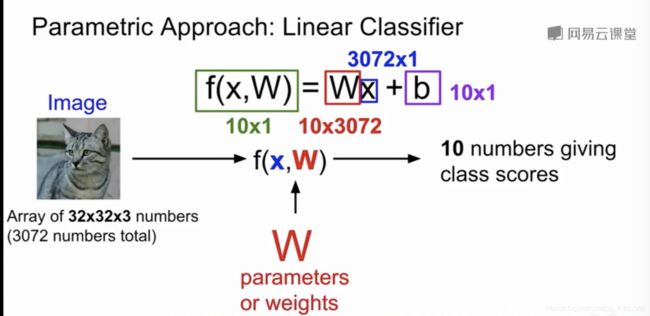
以CIFAR10数据集为例，总共有10类图像，每个图像为32*32*3（3 channels），function的输入是x（3072个像素点组成的向量）和W（通过学习获取的一组权重，图例中因为要使最后的output为10*1的向量，所以此处的W维度为10*3072），b为各个类的偏好值，假如一个数据集中猫的总量较多，该偏好值也会随之更大。最后的10个值为每个类对应的分数，分数越高代表越有可能属于该类。

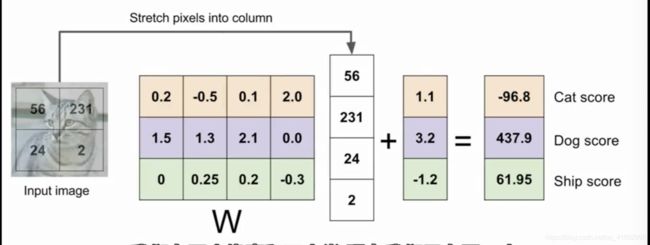
在下图中，图像为2*2（0 channel），将其延展为一个向量，矩阵为4*3（降成3维），加上bias就形成了最终的向量代表分数。

我们可以取某类在矩阵中对应行的数据来还原图像（可以看成一个类对应的template向量），还是以上图为例，cat类在矩阵的第一行，所以cat类对应的每个pixel还原权重是0.2，-0.5，0.1，2.0。如下图就是10个类的还原图像。

使用线性分类器较为的简单，每种类都会对应一个template，如果出现了变体，就会让分类器很难识别。当我们使用神经网络时我们能得到更高的正确率的原因就是因为每个类的识别不再有单个模版限制。

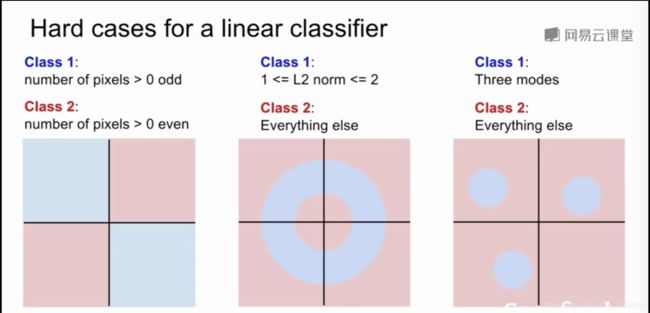
线性分类器的问题是，我们尝试对数据进行线性空间转换，在一个空间里用超平面来对其进行分类，如果数据分布出现上图所示的问题时，通过简单的线性分类无法对其进行有效地划分。

3.Loss function and optimisation

hinge loss in multiple classes SVM

多分类SVM的损失方程如图所示，单个实例的loss value由分类是否精准所决定。我们想让正确分类的值尽量的高于错误分类的值，如图所示的例子中阈值为1，  。 为该分类的值， 为lable对应的分类值。以第一张猫咪的图片为例，syi为3.2，分类为car的loss为 5.1-3.2+1 = 2.9，分类为frog的loss为 -1.7 - 3.2 + 1 = -3.9（即正确分类的值远远大于分类错误的值，此时为负数，结果为0），该实例的loss为2.9 + 0 ，样本的总 loss = sum（loss）/n 。

 

regularization

我们经常在loss上加一项表示正则化，他可以让我们的loss更大，这样在训练模型的时候不会过于拟合训练数据。你对模型的惩罚的目的是为了降低模型的复杂度。

假设我们有w1=（1，0，0，0）和w2=（0.25，0.25，0.25，0.25），, 此时的结果和的结果是相同的，当我们选择L2正则化时会更倾向于w2，因为此时的范数更低，更注重x每个元素对参数的影响。而L1正则化则正好相反，他更鼓励稀疏的矩阵。

softmax

在前面的例子中我们对一输入向量x，给定一参数矩阵w，我们计算出了该图片（实例）对应各个分类的分数，此时我们对该分数并没有直接的定义，只是希望正确分类的分数远远大于分类错误的分数。而使用softmax我们可以将结果映射成概率分布（probablity distribution），当然所有分类的概率之和即为1。

具体的做法是取分类的分数为s，然后取(其作用是使所有的分数都被映射为正数)，随后对所有的分数求和归一化，这样每个分数就被映射成0到1的概率，而所有分类的概率之和为1 。

使用log函数的意义在于log函数是单调递增函数，我们想让正类的概率尽量的高即 log（s）的值尽量的大或者 -log（s）的值尽量的低。此时取负号的意义是为了让其意义更符合损失函数（因为我们的目标是使损失函数尽可能的小）

softmax经常用于将线性回归转化为分类问题上。

 

 

未完待续。。。