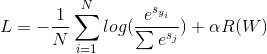cs231n作业（三）softmax分类

一、作业说明

CS231n的第三次作业，要求写一个基于softmax的多分类程序，实现cifar10的多分类功能，程序中应当体现损失函数计算、梯度计算、交叉验证选择参数、权重可视化等功能。

本次作业与第二次作业的基于svm分类要求基本相同，唯一区别在于惩罚函数用的是softmax函数。

二、背景知识

损失函数

                                                      

损失函数分为两部分，前半部分的误差项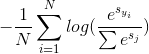和后半部分的正则项。前半部分的误差由模型的输出层进行softmax运算结合交叉熵损失函数得到。后半部分的正则项提升了模型的泛化性能，是正则项系数，本模型中，我们选用的是权重矩阵的F范数。

梯度计算

我们使用分析梯度计算方法。对于属于第类的输入样本，不考虑正则项，模型的loss关于W求梯度为

若为的F范数，

三、程序源码

# -*- coding: utf-8 -*-
"""
Created on Sun Oct 14 16:23:45 2018

@author: Junpeng
"""

import numpy as np
import random
from matplotlib import pylab as plt


#读取cifar10数据
def unpickle(file):
    import pickle
    with open(file, 'rb') as fo:
        dict = pickle.load(fo, encoding='bytes')
    return dict

def sample_training_data(data, labels, num):
        batch_index= np.random.randint(0, data.shape[0], num)
        batch=data[batch_index].T
        batch_labels=labels[batch_index]
        return batch, batch_labels

def get_validation_set(k_fold, num_validation, training_data):
    num_training=np.size(training_data, 0)
    validation_set=random.sample(range(0,num_training),k_fold*num_validation)
    validation_set=np.reshape(validation_set,[num_validation, k_fold])
    return validation_set

#进行数据预处理（归一化并加上偏置）
def preprocessing(data):
    mean=np.mean(data,axis=0)
    std=np.std(data,axis=0)
    data=np.subtract(data,mean)
    data=np.divide(data, std)
    data=np.hstack([data, np.ones((data.shape[0],1))])
    return data

#定义svm损失函数    
def softmax_loss_gradient(w, x, y, alpha):
    socre=np.dot(w, x)
    socre=np.exp(socre)
    socre=socre/np.sum(socre,axis=0)
    
    loss=np.zeros_like(y)
    w_gradient=np.zeros_like(w)
    for index in range(0, x.shape[1]):
        gradient_temp=np.outer(socre[:,index], x[:,index])
        gradient_temp[y[index],:]=(socre[y[index],index]-1)*x[:,index]
        loss[index]=1-socre[y[index],index]
        w_gradient+=gradient_temp
    
    #加入正则化项
    total_loss=np.sum(loss)/(y.shape[0])+0.5*alpha*np.linalg.norm(w)
    w_gradient/=x.shape[1]
    w_gradient+=alpha*w
    return total_loss, w_gradient
   
#跟新权重矩阵
def update(w_gradient, w, learning_rate):
    w += -learning_rate*w_gradient
    return w

#训练函数
def training(info, num_batches, steps, learning_rate, alpha, training_data, training_labels):
    w=np.random.uniform(-0.1, 0.1,(10, training_data.shape[1]))
    loss=np.zeros(steps)
    for inter in range(steps):
        batch, batch_labels=sample_training_data(training_data, training_labels, num_batches) 
        total_loss, gradient=softmax_loss_gradient(w, batch, batch_labels, alpha)
        loss[inter]=total_loss
        update(gradient, w, learning_rate)
        if info==1:
            if np.mod(inter, 50)==0:        
                print('Steps ',inter,' finished. Loss is ', total_loss,' \n')
                plt.figure(0)
                plt.plot(range(steps), loss)
                plt.xlabel('iteration times')
                plt.ylabel('loss')
                plt.savefig('Loss')    
    return w

#测试函数
def testing(w, testing_data, testing_labels):
    socre=np.dot(w, testing_data.T)    
    result=np.argmax(socre,axis=0)
    correct=np.where(result==testing_labels) 
    correct_num=np.size(correct[0])
    accuracy=correct_num/testing_data.shape[0]
    return accuracy

#可视化函数
def visualization(w):
    w_no_bias=w[:,:-1]
    w_reshape=np.reshape(w_no_bias,  [-1,3,32,32])
    w_reshape=w_reshape.transpose((0,2,3,1))
    classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
    for i in range(10):
        w_min=np.min(w_reshape[i,:,:,:])
        w_max=np.max(w_reshape[i,:,:,:])
        w_image=255*(w_reshape[i,:,:,:].squeeze()-w_min)/(w_max-w_min)
        plt.figure(i+1)
        plt.imshow(w_image.astype(np.uint8))
        plt.title(classes[i])
        plt.axis('off')
        image_name=str(i)+'.png'
        plt.savefig(image_name)    

#构建训练数据集
training_data=np.zeros([50000,3072],dtype=np.uint8)
training_filenames=np.zeros([50000],dtype=list)
training_labels=np.zeros([50000],dtype=np.int)
for i in range(0,5):
    file_name='cifar-10-python/cifar-10-batches-py/data_batch_'+str(i+1)
    temp=unpickle(file_name)
    training_data[i*10000+0:i*10000+10000,:]=temp.get(b'data')
    training_filenames[i*10000+0:i*10000+10000]=temp.get(b'filenames')
    training_labels[i*10000+0:i*10000+10000]=temp.get(b'labels')
print('Training data loaded: 50000 samples from 10 categories!\n')

#构建测试数据集
testing_data=np.zeros([10000,3072],dtype=np.uint8)
testing_filenames=np.zeros([10000],dtype=list)
testing_labels=np.zeros([10000],dtype=np.int)
file_name='cifar-10-python/cifar-10-batches-py/test_batch'
temp=unpickle(file_name)
testing_data=temp.get(b'data')
testing_filenames=temp.get(b'filenames')
testing_labels=temp.get(b'labels')
print('Testing data loaded: 10000 samples from 10 categories!\n')

#预处理
training_data=preprocessing(training_data)
testing_data=preprocessing(testing_data)

#从训练集中随机采样出测试集
k_fold=5
num_validation=1000
validation_set=get_validation_set(k_fold, num_validation, training_data)
print('Validation data created from training data: %d folds and %d samples for each fold.\n '%(k_fold, num_validation))

#超参数候选范围
learning_rate_candidate=[1e-2, 5e-3, 1e-3, 5e-4, 1e-4, 5e-5, 1e-5]
alpha_candidate=[0.1, 0.5, 1, 5, 10, 20]


#进行k-fold交叉验证
validation_accuracy=np.zeros([len(learning_rate_candidate),len(alpha_candidate), k_fold])
for i, learning_rate in enumerate(learning_rate_candidate):
    for j, alpha in enumerate(alpha_candidate):
        for k in range(k_fold):
            validation_training=np.delete(validation_set,0,axis=1)
            validation_training=np.reshape(validation_training,[(k_fold-1)*num_validation])
            validation_training_labels=training_labels[validation_training]
            validation_training=training_data[validation_training,:]
            validation_testing=training_data[validation_set[:,k],:]
            validation_testing_labels=training_labels[validation_set[:,k]]
            w=training(0, 32, 500, learning_rate, alpha, validation_training, validation_training_labels)
            accuracy=testing(w, validation_testing, validation_testing_labels)
            validation_accuracy[i][j][k]=accuracy
        print('learning rate %e alpha %e accuracy: %f' % (learning_rate, alpha, np.mean(validation_accuracy[i][j][:])))
par =np.where(np.mean(validation_accuracy,2)==np.max(np.mean(validation_accuracy,2)))           
learning_rate=learning_rate_candidate[int(par[0])]
alpha=alpha_candidate[int(par[1])]
print('The chosen parameters: learning rate %e alpha %f'% (learning_rate, alpha))

#训练过程
print('Training...\n')
num_batches=128
steps=1500
info=1
w=training(1, num_batches, steps, learning_rate, alpha, training_data, training_labels)
   
#测试阶段
print('Testing...\n')
accuracy=testing(w, testing_data, testing_labels)
print('accuracy is ',accuracy)

#可视化权重矩阵
visualization(w)

四、程序输出

样本读取

Training data loaded: 50000 samples from 10 categories!

Testing data loaded: 10000 samples from 10 categories!

Validation data created from training data: 5 folds and 1000 samples for each fold.
 

交叉验证

learning rate 1.000000e-02 alpha 1.000000e-01 accuracy: 0.388000
learning rate 1.000000e-02 alpha 5.000000e-01 accuracy: 0.367600
learning rate 1.000000e-02 alpha 1.000000e+00 accuracy: 0.334600
learning rate 1.000000e-02 alpha 5.000000e+00 accuracy: 0.275800
learning rate 1.000000e-02 alpha 1.000000e+01 accuracy: 0.246000
learning rate 1.000000e-02 alpha 2.000000e+01 accuracy: 0.230200
learning rate 5.000000e-03 alpha 1.000000e-01 accuracy: 0.356200
learning rate 5.000000e-03 alpha 5.000000e-01 accuracy: 0.390000
learning rate 5.000000e-03 alpha 1.000000e+00 accuracy: 0.389800
learning rate 5.000000e-03 alpha 5.000000e+00 accuracy: 0.310200
learning rate 5.000000e-03 alpha 1.000000e+01 accuracy: 0.299600
learning rate 5.000000e-03 alpha 2.000000e+01 accuracy: 0.271200
learning rate 1.000000e-03 alpha 1.000000e-01 accuracy: 0.251600
learning rate 1.000000e-03 alpha 5.000000e-01 accuracy: 0.271000
learning rate 1.000000e-03 alpha 1.000000e+00 accuracy: 0.297000
learning rate 1.000000e-03 alpha 5.000000e+00 accuracy: 0.351200
learning rate 1.000000e-03 alpha 1.000000e+01 accuracy: 0.341000
learning rate 1.000000e-03 alpha 2.000000e+01 accuracy: 0.317200
learning rate 5.000000e-04 alpha 1.000000e-01 accuracy: 0.218000
learning rate 5.000000e-04 alpha 5.000000e-01 accuracy: 0.222400
learning rate 5.000000e-04 alpha 1.000000e+00 accuracy: 0.234800
learning rate 5.000000e-04 alpha 5.000000e+00 accuracy: 0.300000
learning rate 5.000000e-04 alpha 1.000000e+01 accuracy: 0.326400
learning rate 5.000000e-04 alpha 2.000000e+01 accuracy: 0.317600
learning rate 1.000000e-04 alpha 1.000000e-01 accuracy: 0.143600
learning rate 1.000000e-04 alpha 5.000000e-01 accuracy: 0.142600
learning rate 1.000000e-04 alpha 1.000000e+00 accuracy: 0.153600
learning rate 1.000000e-04 alpha 5.000000e+00 accuracy: 0.158200
learning rate 1.000000e-04 alpha 1.000000e+01 accuracy: 0.164800
learning rate 1.000000e-04 alpha 2.000000e+01 accuracy: 0.192400
learning rate 5.000000e-05 alpha 1.000000e-01 accuracy: 0.134400
learning rate 5.000000e-05 alpha 5.000000e-01 accuracy: 0.124400
learning rate 5.000000e-05 alpha 1.000000e+00 accuracy: 0.122000
learning rate 5.000000e-05 alpha 5.000000e+00 accuracy: 0.133800
learning rate 5.000000e-05 alpha 1.000000e+01 accuracy: 0.128600
learning rate 5.000000e-05 alpha 2.000000e+01 accuracy: 0.117400
learning rate 1.000000e-05 alpha 1.000000e-01 accuracy: 0.107400
learning rate 1.000000e-05 alpha 5.000000e-01 accuracy: 0.098800
learning rate 1.000000e-05 alpha 1.000000e+00 accuracy: 0.109000
learning rate 1.000000e-05 alpha 5.000000e+00 accuracy: 0.094600
learning rate 1.000000e-05 alpha 1.000000e+01 accuracy: 0.102000
learning rate 1.000000e-05 alpha 2.000000e+01 accuracy: 0.091000
The chosen parameters: learning rate 5.000000e-03 alpha 0.500000

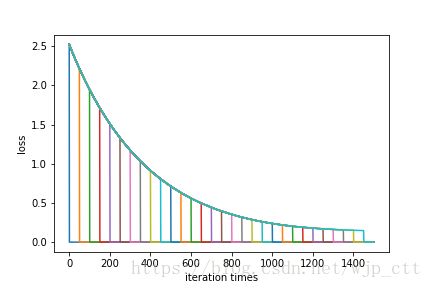
训练

Training...

Steps  0  finished. Loss is  2.5211913793066967  

Steps  50  finished. Loss is  2.2133148649570606  

Steps  100  finished. Loss is  1.9468842156735475  

Steps  150  finished. Loss is  1.7137559723219886  

Steps  200  finished. Loss is  1.5092535079342537  

Steps  250  finished. Loss is  1.3297739598351996  

Steps  300  finished. Loss is  1.172304386362182  

Steps  350  finished. Loss is  1.0338897029357432  

Steps  400  finished. Loss is  0.9124986310025536  

Steps  450  finished. Loss is  0.8059949531491087  

Steps  500  finished. Loss is  0.712542573114957  

Steps  550  finished. Loss is  0.6306623820716823  

Steps  600  finished. Loss is  0.559015467696233  

Steps  650  finished. Loss is  0.49633439685305897  

Steps  700  finished. Loss is  0.4419771695763197  

Steps  750  finished. Loss is  0.39456089617289625  

Steps  800  finished. Loss is  0.35357162509393  

Steps  850  finished. Loss is  0.3175805866378341  

Steps  900  finished. Loss is  0.2865592234227146  

Steps  950  finished. Loss is  0.2600502528751914  

Steps  1000  finished. Loss is  0.23732592916768477  

Steps  1050  finished. Loss is  0.21836094961573738  

Steps  1100  finished. Loss is  0.20175617584270394  

Steps  1150  finished. Loss is  0.1893912255359981  

Steps  1200  finished. Loss is  0.17838700856962858  

Steps  1250  finished. Loss is  0.16844531608417598  

Steps  1300  finished. Loss is  0.16232993994537892  

Steps  1350  finished. Loss is  0.1551975246600514  

Steps  1400  finished. Loss is  0.15052720902325553  

Steps  1450  finished. Loss is  0.14682188324294737  

测试

Testing...

accuracy is  0.388

 

 

 

五、结果说明

经过交叉验证，最优正则化系数和学习率的值为0.5和0.005。在训练过程中损失函数值不断下降。最终模型在10000张图片上的测试结果为38.8%。考虑到我们是直接基于像素特征进行训练的，这个结果可以接受。可以通过提取比像素特征更一般的特征提升测试结果。该结果比svm损失函数结果好。