【论文翻译】用知识图谱的多任务特征学习来增强推荐
Wang H, Zhang F, Zhao M, et al. Multi-task feature learning for knowledge graph enhanced recommendation[C]//The World Wide Web Conference. 2019: 2000-2010.
原文链接:https://arxiv.org/pdf/1901.08907.pdf
代码实现:https://github.com/hwwang55/MKR
摘要
在实际推荐场景中,协同过滤通常会遇到稀疏性和冷启动问题,因此,研究人员和工程师通常使用辅助信息来解决这些问题并提高推荐系统的性能。在本文中,我们将知识图谱视为辅助信息的来源。我们提出了MKR,一种用于知识图谱增强推荐的多任务特征学习方法。MKR是一个深层的端到端框架,它利用知识图谱嵌入任务来辅助推荐任务。这两个任务由交叉压缩单元关联,交叉压缩单元自动共享潜在特征,并学习推荐系统中的项目与知识图谱中的实体之间的高级交互。我们证明交叉压缩单元具有足够的多项式逼近能力,并且证明了MKR是推荐系统和多任务学习的几种代表性方法的广义框架。通过在现实世界数据集上进行的广泛实验,我们证明了MKR在最新的基线之上,在电影,书籍,音乐和新闻推荐方面取得了可观的收益。即使用户-物品交互稀疏,MKR也能保持良好的性能。
关键词
推荐系统;知识图谱;多任务学习
1 介绍
推荐系统(RS)旨在解决信息爆炸问题并满足用户的个性化兴趣。最受欢迎的推荐技术之一是协同过滤协作过滤(CF)[11],它利用用户的历史互动并根据他们的共同偏好进行推荐。但是,基于CF的方法通常遭受用户项目交互的稀疏性和冷启动问题。因此,研究人员建议使用推荐系统中的辅助信息,包括社交网络[10],属性[30]和多媒体(例如,文本[29],图像[40])。知识图谱(KGs)是RS的一种附带信息,通常包含丰富的事实和有关项目的联系。最近,研究人员提出了一些学术和商业KG,例如NELL1,DBpedia2,Google Knowledge Graph3和Microsoft Satori4。由于KG的高维性和异质性,通常通过知识图嵌入(KGE)方法对其进行预处理[27],该方法将实体和关系嵌入到低维向量空间中,同时保留其固有结构。
现有的知识图谱感知方法
受到在各种任务中成功应用KG的启发,研究人员最近尝试利用KG来提高推荐系统的性能[31,32,39,40,45]。个性化实体推荐(PER)[39]和带有组套索的分解机(FMG)[45]将KG视为异构信息网络,并提取基于元路径/元图的潜在特征来表示用户和项目之间的连通性不同类型的关系路径/图形。应当注意,PER和FMG严重依赖于手动设计的元路径/元图,这限制了其在通用推荐方案中的应用。深度知识感知网络(DKN)[32]设计了一个CNN框架,将实体嵌入与单词嵌入相结合以进行新闻推荐。但是,在使用DKN之前需要实体嵌入,这导致DKN缺乏端到端的训练方式。关于DKN的另一个问题是,它几乎不能合并文字以外的辅助信息。RippleNet [31]是一种类似于内存网络的模型,可以在KG中传播用户的潜在偏好并探究他们的层次兴趣。但是,关系的重要性在RippleNet中几乎没有体现出来,因为关系R的嵌入矩阵很难训练为以二次形式 v T R h v^TRh vTRh捕捉重要性(v和h是两个实体的嵌入向量)。协作知识库嵌入(CKE)[40]在一个统一的框架中将CF与结构知识,文本知识和视觉知识结合在一起。但是,CKE中的KGE模块(即TransR [13])更适合于图内应用(例如知识图谱补全和实体链接预测),而不是推荐应用。另外,在贝叶斯框架下的CKE中,CF模块和KGE模块之间的连接松散,KG对于推荐系统的监督不太明显。
提出的方法
为了解决先前工作的局限性,我们提出了MKR,一种用于知识图增强推荐的多任务学习(MTL)方法。MKR是一个通用的端到端深度推荐框架,旨在利用KGE任务来辅助推荐任务 5 ^5 5(如实验部分所示,KGE任务也可以凭经验从推荐任务中受益)。注意,这两个任务不是相互独立的,而是高度相关的,因为RS中的一项可能与KG中的一个或多个实体相关联。因此,一个项目及其对应的实体在RS和KG中可能具有相似的邻近结构,并在低级和非特定于任务的潜在特征空间中共享相似的特征[15]。我们将在实验部分进一步验证相似性。为了建模项目和实体之间的共享功能,我们在MKR中设计了一个交叉压缩单元。交叉和压缩单元显式地建模项目和实体要素之间的高级交互,并自动控制两个任务的交叉知识转移。通过交叉压缩单元,项目和实体的表示形式可以相互补充,从而在避免拟合噪声和提高泛化性方面均有助于完成两项任务。可以通过以不同的频率交替优化两个任务来训练整个框架,这使MKR在实际推荐场景中具有很高的灵活性和适应性。我们探讨了MKR的表达能力,并通过理论分析表明,交叉压缩单元能够近似项和实体之间足够高阶的特征相互作用。
我们还表明,MKR是一种基于推荐系统和多任务学习的几种代表性方法的通用框架,包括分解机[22,23],深度和跨网络[34]和跨针网络[18]。根据经验,我们在四个推荐方案中评估我们的方法,即电影,书籍,音乐和新闻推荐。结果表明,MKR在点击率(CTR)预测(例如,电影的AUC平均提高11.6%)和前K推荐(例如,Recall @ 10为66.4%)方面都比最新基准有了实质性的提高 图书的平均改善)
贡献
值得注意的是,本文中研究的问题也可以建模为跨域推荐[26]或转移学习[21],因为我们更加关注推荐任务的性能。但是,关键的观察结果是,尽管跨域推荐和转移学习对目标域具有单一目标,但它们的损失函数仍包含用于测量源域中数据分布或两个域之间相似度的约束项。在我们提出的MKR中,KGE任务明确用作约束项,以为推荐系统提供正则化。我们想强调的是,本文的主要贡献是将问题准确地建模为多任务学习:如理论分析和实验结果所示,我们发现跨任务相似性不仅对推荐系统有用,而且知识图嵌入比跨域推荐和转移学习更进一步。
2 我们的方法
在本节中,我们首先制定知识图增强的推荐问题,然后介绍MKR的框架,并详细介绍交叉压缩单元,推荐模块和KGE模块的设计。我们最后讨论了MKR的学习算法。
2.1 问题的形式
我们在本文中制定了知识图谱增强推荐问题,在典型的推荐方案中,我们有一组M个用户 U = { u 1 , u 2 , . . . , u M } U=\{u_1,u_2,...,u_M\} U={u1,u2,...,uM}和一组N个物品 V = { v 1 , v 2 , . . . , v N } V = \{v_1,v2,...,v_N\} V={v1,v2,...,vN}。用户-物品交互矩 Y ∈ R M × N Y∈R^{M×N} Y∈RM×N是根据用户的隐式反馈定义的,其中 y u v y_uv yuv = 1表示用户u对物品v具有行为,例如点击,观看,浏览或购买行为。否则 y u v y_uv yuv = 0。此外,我们还可以访问知识图谱G,它由实体-关系-实体三元组(h, r, t)组成。在这里,h,r和t分别表示知识三元组的头部,关系和尾部。例如,三元组(Quentin Tarantino, film.director.film, Pulp Fiction)说明了昆汀·塔伦蒂诺执导电影低俗小说的事实。在许多推荐场景中,项目v∈V可能与G中的一个或多个实体相关联。例如,在电影推荐中,Pulp Fiction与它在KG中的名字相关联,而在新闻推荐中,新闻与标题“特朗普承诺在技术会议期间向硅谷提供援助”与一个幼稚园中的“唐纳德·特朗普”和“硅谷”相关。给定用户与项目的交互矩阵Y以及知识图G,我们旨在预测用户u是否对项目v具有潜在的兴趣,而他之前从未与之交互。
2.2 架构
MKR的框架如图1(a)所示。 MKR由三个主要组件组成:推荐模块,KGE模块和交叉压缩单元。 (1)左侧的推荐模块将用户和物品作为输入,并使用多层感知器(MLP)和交叉压缩单元分别为用户和物品提取简短特征和密集特征。然后将提取的特征一起馈入另一个MLP,以输出预测的概率。 (2)与左侧类似,右侧的KGE模块也使用多层从知识三元组的头部和关系中提取特征,并在得分函数f和真实尾部的监督下输出预测尾部的表示。 (3)推荐模块和KGE模块通过特殊设计的交叉压缩单元桥接。提议的单位可以自动学习推荐系统和KG中实体的项目的高级特征交互。
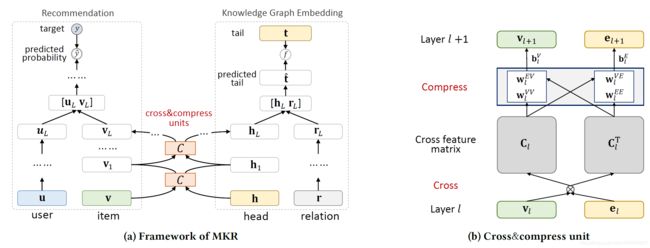 图1:(a)MKR的框架。左侧和右侧分别示出了推荐模块和KGE模块,它们由交叉和压缩单元桥接。 (b)交叉压缩单元的图示。交叉和压缩单元通过交叉操作从项目和实体向量生成交叉特征矩阵,并通过压缩操作将其向量输出到下一层。
图1:(a)MKR的框架。左侧和右侧分别示出了推荐模块和KGE模块,它们由交叉和压缩单元桥接。 (b)交叉压缩单元的图示。交叉和压缩单元通过交叉操作从项目和实体向量生成交叉特征矩阵,并通过压缩操作将其向量输出到下一层。
2.3 交叉压缩单元
为了建模物品与实体之间的要素交互,我们在MKR框架中设计了一个交叉压缩单元。如图1(b)所示,对于第v项及其关联实体e,我们首先从层l构造其潜在特征 v l ∈ R d v_l∈R^d vl∈Rd和 e l ∈ R d e_l∈R^d el∈Rd的d×d成对相互作用:
C l = v l e l T = [ v l ( 1 ) e l ( 1 ) . . . v l ( 1 ) e l ( d ) . . . . . . v l ( d ) e l ( 1 ) . . . v l ( d ) e l ( d ) ] (1) C_l=v_le_l^T=\begin{bmatrix} v_l^{(1)}e_l^{(1)} & ... & v_l^{(1)}e_l^{(d)} \\ ... & & ... \\v_l^{(d)}e_l^{(1)} & ... & v_l^{(d)}e_l^{(d)} \end{bmatrix} \tag{1} Cl=vlelT=⎣⎢⎡vl(1)el(1)...vl(d)el(1)......vl(1)el(d)...vl(d)el(d)⎦⎥⎤(1)
其中C_l∈R^{d×d}是层l的交叉特征矩阵,d是隐藏层的尺寸。之所以称为交叉运算,是因为显式地建模了物品v及其关联实体e之间的每个可能的特征相互作用 v l ( i ) e l ( j ) , ∀ ( i , j ) ∈ { 1 , . . . , d } 2 v_l^{(i)}e_l^{(j)},\forall(i,j)\in\{1,...,d\}^2 vl(i)el(j),∀(i,j)∈{1,...,d}2在交叉特征矩阵中明确建模了物品v及其关联实体e之间的关系。然后,通过将交叉特征矩阵投影到它们的潜在表示空间中,我们输出下一层的物品和实体的特征向量:
v l + 1 = C l w l V V + C l T w l E V + b l V = v l e l T w l V V + e l v l T w l E V + b l V , e l + 1 = C l w l V E + C l T w l E E + b l E = v l e l T w l V E + e l v l T w l E E + b l E , (2) v_{l+1}=C_lw_l^{VV}+C_l^Tw_l^{EV}+b_l^V=v_le_l^Tw_l^{VV}+e_lv_l^Tw_l^{EV}+b_l^V,\\ e_{l+1}=C_lw_l^{VE}+C_l^Tw_l^{EE}+b_l^E=v_le_l^Tw_l^{VE}+e_lv_l^Tw_l^{EE}+b_l^E,\tag{2} vl+1=ClwlVV+ClTwlEV+blV=vlelTwlVV+elvlTwlEV+blV,el+1=ClwlVE+ClTwlEE+blE=vlelTwlVE+elvlTwlEE+blE,(2)
其中 w l . . ∈ R d w_l^{..}\in R^d wl..∈Rd且 b l . ∈ R d b_l^.\in R^d bl.∈Rd是可训练的权重和偏差向量。这被称为压缩操作,因为权重向量将交叉特征矩阵从 R d × d R^{d×d} Rd×d空间投影回特征空间 R d R^d Rd。注意在等式(2)中,为了对称起见,沿水平和垂直方向(通过对 C l C_l Cl和 C l ⊤ C^⊤_l Cl⊤进行运算)压缩了交叉特征矩阵,但是我们将在3.2节中提供更多有关设计的见解。为简单起见,交叉压缩单元表示为:
[ v l + 1 , e l + 1 ] = C ( v l , e l ) (3) [v_{l+1}, e_{l+1}]=C(v_l,e_l) \tag{3} [vl+1,el+1]=C(vl,el)(3)
在下面的文章中,我们使用后缀[v]或[e]区分其两个输出。通过交叉压缩单元,MKR可以自适应地调整知识转移的权重并了解两个任务之间的相关性。应当注意,交叉压缩单元仅应存在于MKR的低层中,如图1(a)所示。这是因为:
(1)在深层架构中,功能通常会沿着网络从通用转换为特定功能,并且随着任务不相似性的增加,功能可传递性在更高层中会大大下降[38]。因此,共享高级层可能存在负迁移的风险,尤其是对于MKR中的异构任务而言。
(2)在MKR的高层中,物品特征与用户特征混合,而实体特征与关系特征混合。由于混合功能没有明确的关联,因此不适合共享。
2.4 推荐模块
MKR中推荐模块的输入由两个原始特征向量u和v组成,分别描述用户u和项目v。根据应用场景,可以将u和v定制为一键式ID [8],属性[30],词袋[29]或它们的组合。
给定用户u的原始特征向量u,我们使用L层MLP提取其潜在的压缩特征 6 ^6 6(我们在等式中使用指数符号L为简单起见,本文中的(4)和下面的方程式使用,但是请注意,L层的参数实际上是不同的。):
u L = M ( M ( . . . M ( u ) ) ) = M L ( u ) , (4) u_L=M(M(...M(u)))=M^L(u), \tag{4} uL=M(M(...M(u)))=ML(u),(4)
其中 M ( x ) = σ ( W x + b ) M(x)=\sigma(W_x+b) M(x)=σ(Wx+b)是具有权重W,偏差b和非线性激活函数 σ ( ⋅ ) σ(·) σ(⋅)的完全连接的神经网络层 7 ^7 7(在推荐模块中探索更精细的层设计是未来工作的重要方向。)。对于物品v,我们使用L个交叉压缩单元提取其特征:
v L = E e 〜 S ( v ) [ C L ( v , e ) [ v ] , (5) v_L = E_{e〜S(v)}[C^L(v,e)[v], \tag{5} vL=Ee〜S(v)[CL(v,e)[v],(5)
其中S(v)是项目相关实体的集合 v。
在获得用户u的潜在特征 u L u_L uL和物品v的潜在特征 v L v_L vL之后,我们通过预测函数 f R f_{R} fR(例如内部产品或H层MLP)将这两种途径结合起来。用户u参与项目v的最终预测概率为:
y ^ u v = σ ( f R S ( u L , v L ) ) (6) \hat{y}_{uv}=\sigma(f_{RS}(u_L,v_L)) \tag{6} y^uv=σ(fRS(uL,vL))(6)
2.5 知识图谱嵌入模块
知识图嵌入是将实体和关系嵌入到连续的向量空间中,同时保留其结构。最近,研究人员提出了许多KGE方法,包括翻译距离模型[2,13]和语义匹配模型[14,19]。在MKR中,我们为KGE模块提出了一种深度语义匹配架构。与推荐模块类似,对于给定的知识三元组(h, r, t),我们首先利用多个交叉压缩单元和非线性层来处理头部h和关系r(包括ID [13],类型[36] ],文字说明[35]等)。然后将它们的潜在特征连接在一起,然后是用于预测尾部t的K层MLP:
h L = E v ~ S ( h ) [ C L ( v , h ) [ e ] ] , r L = M L ( r ) , t ^ = M K ( [ h L r L ] ) (7) h_L = E_{v~S(h)}[C^L(v,h)[e]],\\ r_L = M^L(r),\\ \tag{7} \hat{t} = M^K(\begin{bmatrix} h_L \\r_L\end{bmatrix} ) hL=Ev~S(h)[CL(v,h)[e]],rL=ML(r),t^=MK([hLrL])(7)
其中S(h)是实体h的关联项的集合, t ^ \hat{t} t^是尾t的预测向量。最后,使用得分(相似度)函数 f K G f_{KG} fKG计算三元组 ( h , r , t ) (h,r,t) (h,r,t)的得分:
s c o r e ( h , r , t ) = f K G ( t , t ^ ) . (8) score(h,r,t)= f_{KG}(t,\hat{t}).\tag{8} score(h,r,t)=fKG(t,t^).(8)其中t是真实特征t的向量。在本文中,我们使用归一化内积 f K G ( t , t ^ ) = σ ( t ⊤ , t ^ ) f_{KG}(t,\hat{t})=σ(t^⊤,\hat{t}) fKG(t,t^)=σ(t⊤,t^)作为得分函数的选择[18],但是在这里也可以应用其他形式的(非)相似性度量,例如KullbackĂŞLeibler分歧。
2.6 学习算法
MKR的完全损失函数如下:
L = L R S + L K G + L R E G = ∑ u ∈ U , v ∈ V J ( y ^ u v , y u v ) − λ 1 ( ∑ ( h , r , t ) ∈ G s c o r e ( h , r , t ) − ∑ ( h ′ , r ′ , t ′ ) ∉ G s c o r e ( h ′ , r ′ , t ′ ) ) + λ 2 ∣ ∣ W ∣ ∣ 2 2 (9) L = L_{RS} + L_{KG}+ L{REG} =\sum_{u\in U,v\in V}J(\hat{y}_{uv},y_{uv})\\−λ_1(\sum_{(h,r,t)\in G}score(h,r,t)-\sum_{(h',r',t')\notin G}score(h',r',t')) \\ +\lambda_2||W||_2^2\tag{9} L=LRS+LKG+LREG=u∈U,v∈V∑J(y^uv,yuv)−λ1((h,r,t)∈G∑score(h,r,t)−(h′,r′,t′)∈/G∑score(h′,r′,t′))+λ2∣∣W∣∣22(9)
在等式中 (9),第一个项在推荐模块中度量损失,其中u和v分别遍历用户集和物品集,而J是交叉熵函数。第二项在KGE模块中计算损失,我们的目标是增加所有真实三元组的得分,同时减少所有虚假三元组的得分。最后一项是防止过度拟合的正则化项, λ 1 λ_1 λ1和 λ 2 λ_2 λ2是平衡参数。( λ 1 λ_1 λ1可以看作是两个任务的两个学习率之比。)
注意方程(9)中的损失函数,遍历所有可能的用户项对和知识三元组。为了使计算更有效,遵循[17],我们在训练期间使用负采样策略。算法1中介绍了MKR的学习算法,其中训练时期包括两个阶段:推荐任务(第3-7行)和KGE任务(第8-10行)。在每次迭代中,我们会先对推荐任务重复训练t次(t是超参数,通常t> 1),然后再在每个阶段对KGE任务进行训练,因为我们更加专注于提高推荐效果。我们将在实验部分讨论t的选择。
'''
算法1 MKR的多任务训练
输入:交互矩阵Y,知识图谱G
输出:预测函数F(u,v|Θ,Y,G)
'''
def train(args, data, show_loss, show_topk):
n_user, n_item, n_entity, n_relation = data[0], data[1], data[2], data[3]
train_data, eval_data, test_data = data[4], data[5], data[6]
kg = data[7]
model = MKR(args, n_user, n_item, n_entity, n_relation)
# top-K evaluation settings
user_num = 100
k_list = [1, 2, 5, 10, 20, 50, 100]
train_record = get_user_record(train_data, True)
test_record = get_user_record(test_data, False)
user_list = list(set(train_record.keys()) & set(test_record.keys()))
if len(user_list) > user_num:
user_list = np.random.choice(user_list, size=user_num, replace=False)
item_set = set(list(range(n_item)))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(args.n_epochs):
# RS training
np.random.shuffle(train_data)
start = 0
while start < train_data.shape[0]:
_, loss = model.train_rs(sess, get_feed_dict_for_rs(model, train_data, start, start + args.batch_size))
start += args.batch_size
if show_loss:
print(loss)
# KGE training
if step % args.kge_interval == 0:
np.random.shuffle(kg)
start = 0
while start < kg.shape[0]:
_, rmse = model.train_kge(sess, get_feed_dict_for_kge(model, kg, start, start + args.batch_size))
start += args.batch_size
if show_loss:
print(rmse)
# CTR evaluation
train_auc, train_acc = model.eval(sess, get_feed_dict_for_rs(model, train_data, 0, train_data.shape[0]))
eval_auc, eval_acc = model.eval(sess, get_feed_dict_for_rs(model, eval_data, 0, eval_data.shape[0]))
test_auc, test_acc = model.eval(sess, get_feed_dict_for_rs(model, test_data, 0, test_data.shape[0]))
print('epoch %d train auc: %.4f acc: %.4f eval auc: %.4f acc: %.4f test auc: %.4f acc: %.4f'
% (step, train_auc, train_acc, eval_auc, eval_acc, test_auc, test_acc))
# top-K evaluation
if show_topk:
precision, recall, f1 = topk_eval(
sess, model, user_list, train_record, test_record, item_set, k_list)
print('precision: ', end='')
for i in precision:
print('%.4f\t' % i, end='')
print()
print('recall: ', end='')
for i in recall:
print('%.4f\t' % i, end='')
print()
print('f1: ', end='')
for i in f1:
print('%.4f\t' % i, end='')
print('\n')
3 理论分析
在本节中,我们证明交叉压缩单元具有足够的多项式逼近能力。我们还表明,MKR是一个基于推荐系统和多任务学习的几种代表性方法的通用框架。
3.1多项式逼近
根据Weierstrass逼近定理[25],在一定平滑度假设下的任何函数都可以通过多项式逼近为任意精度。因此,我们研究了交叉压缩单元高阶交互逼近的能力。我们证明了交叉压缩单元可以对物品-实体特征交互的顺序进行建模,直至达到指数级:
定理1:
分别用 v = [ v 1 , ⋅ ⋅ ⋅ , v d ] ⊤ v = [v_1,···,v_d]^⊤ v=[v1,⋅⋅⋅,vd]⊤和 e = [ e 1 , ⋅ ⋅ ⋅ , e d ] ⊤ e = [e_1,···,e _d]^⊤ e=[e1,⋅⋅⋅,ed]⊤表示项目和实体在MKR网络中的输入。
∣ ∣ v ∣ ∣ 1 ||v_||_1 ∣∣v∣∣1和 ∣ ∣ e L ∣ ∣ 1 ||e_L||_1 ∣∣eL∣∣1( v L v_L vL和 e L e_L eL的L1-范数)中具有最大程度的关于v和e的交叉项是 k α , β v 1 α 1 ⋅ ⋅ ⋅ v d α d e 1 β 1 ⋅ ⋅ ⋅ e d β d k_α,β^{v_1^{\alpha_1}}···v^{α_d}_de^{β1}_1···e^{βd}_d kα,βv1α1⋅⋅⋅vdαde1β1⋅⋅⋅edβd,
其中 k α , β ∈ R , α i , β i ∈ N k_{α,β}\in R,α_i,β_i∈N kα,β∈R,αi,βi∈N对于 i ∈ { 1 , ⋅ ⋅ ⋅ , d } , α 1 + ⋅ ⋅ ⋅ + α d = 2 L − 1 , β 1 + ⋅ ⋅ ⋅ + β d = 2 L − 1 ( L ≥ 1 , v 0 = v , e 0 = e ) i\in \{1,···,d\}, α_1+···+α_d= 2_{L-1},β_1+···+β_d= 2^{L-1}( L≥1,v_0 = v,e_0 = e) i∈{1,⋅⋅⋅,d},α1+⋅⋅⋅+αd=2L−1,β1+⋅⋅⋅+βd=2L−1(L≥1,v0=v,e0=e)
在推荐系统中, ∏ i = 1 d \prod_{i=1}^d ∏i=1d也被称为组合特征,因为它测量多个原始特征的相互作用。定理1指出,交叉压缩单元可以自动对物品和实体的组合特征进行建模,以获得足够高的阶数,这证明了与现有工作(例如Wide&Deep [3],分解机[22、23]和DCN)相比,MKR具有更好的近似能力[34]。定理1的证明在附录中提供。注意,定理1给出了交叉压缩单元多项式逼近能力的理论视图,而不是为其实际性能提供保证。我们将在实验部分中凭经验评估交叉压缩单元。
3.2 代表方法的统一视图
接下来,我们通过展示它们是MKR的受限制版本或在理论上与MKR相关的模型,在推荐系统和多任务学习中提供几种代表模型的统一视图。这证明了交叉压缩单元的设计合理,并从概念上解释了与基准相比其强大的经验性能。
3.2.1因式分解机
分解机[22,23]是推荐系统的通用方法。在给定输入特征向量的情况下,FM使用分解参数对输入向量中变量之间的所有交互进行建模,从而能够估计具有稀疏性的问题(例如推荐系统)中的交互。 2度分解机的模型方程式定义为:
y ^ ( x ) = w 0 + ∑ i = 1 d w i x i + ∑ i = 1 d ∑ j = i + 1 d < v i , v j > x i x j , (10) \hat{y}(x)=w_0+\sum_{i=1}^dw_ix_i+\sum^{d}_{i=1}\sum_{j=i+1}^{d}
其中 x i x_i xi是输入向量x的第i个单位, w ⋅ w_· w⋅是权重标量, v ⋅ v_· v⋅是权重向量, ⟨ ⋅ , ⋅ ⟩ ⟨·,·⟩ ⟨⋅,⋅⟩是两个向量的点积。我们证明FM的本质在概念上类似于1层交叉压缩单元:
命题1: v 1 v_1 v1和 e 1 e_1 e1的L1范数可以表示为以下形式:
∣ ∣ v 1 ∣ ∣ 1 ( o r ∣ ∣ e 1 ∣ ∣ 1 ) = ∣ b + ∑ i = 1 d ∑ j = 1 d < w i , w j > v i e j ∣ , (11) ||v_1||_1(or||e_1||_1)=|b+\sum_{i=1}^d\sum_{j=1}^d
其中 < w i , w j > = w i + w j
有趣的是,没有像FM中那样将 x i x j x_ix_j xixj的权重参数分解为两个矢量的点积,而是将 v i e j v_ie_j viej的权重分解为交叉压缩单元中两个标量的和,以减少参数数量并增加模型的鲁棒性。
3.2.2 Deep&Cross网络
DCN [34]通过引入以下层来学习显式和高阶叉形特征:
x l + 1 = x 0 x l T w l + x l + b l , (12) x_{l+1}=x_0x_l^Tw_l+x_l+b_l, \tag{12} xl+1=x0xlTwl+xl+bl,(12)其中 x l , w l x_l,w_l xl,wl和 b l b_l bl是第l阶的表示,权重和偏差层。我们通过以下命题证明DCN与MKR之间的联系:
命题2。在等式(2)中的 v l + 1 v_{l +1} vl+1的公式,如果我们将第一项中的 w V V w_{VV} wVV限制为满足 e l ⊤ w l V V = 1 e^⊤_lw^{VV}_l = 1 el⊤wlVV=1并将第二项中的 e l e_l el限制为 e 0 e_0 e0(并对 e l + 1 e_{l + 1} el+1施加类似的限制),则交叉压缩单元在概念上是等效的多任务学习意义上的DCN层:
v l + 1 = e 0 v l T w l E V + v l + b l V , e l + 1 = v 0 e l T w l V E + e l + b l E (13) v_{l+1}=e_0v^T_lw_l^{EV}+v_l+b_l^V,\\ e_{l+1}=v_0e^T_lw_l^{VE}+e_l+b_l^E\tag{13} vl+1=e0vlTwlEV+vl+blV,el+1=v0elTwlVE+el+blE(13)
可以证明,上述等效DCN形式的多项式逼近能力(即vl和el的最大交叉项度)为O(l),比具有O(2l)逼近能力的原始交叉压缩单元弱 。
3.2.3 Cross-stitch网络
Cross-stitch[18]是卷积网络中的多任务学习模型,其中设计的Cross-stitch单元可以学习两个任务之间共享的和特定于任务的表示的组合。具体来说,给定两个任务的第l层的两个激活图 x A x_A xA和 x B x_B xB,Cross-stitch网络将学习两个输入激活的线性组合 A ~ \tilde{A} A~和 B ~ \tilde{B} B~,并将这些组合作为输入提供给下一层的过滤器。激活图中位置(i, j)的公式为:
[ x ~ A i j x ~ A i j ] = [ α A A α A B α B A α B B ] [ x A i j x B i j ] (14) \begin{bmatrix} \tilde{x}_A^{ij} \\\tilde{x}_A^{ij}\end{bmatrix} =\begin{bmatrix} \alpha_{AA} & \alpha_{AB}\\\alpha_{BA} & \alpha_{BB} \end{bmatrix}\begin{bmatrix} x_A^{ij} \\ x_B^{ij} \end{bmatrix} \tag{14} [x~Aijx~Aij]=[αAAαBAαABαBB][xAijxBij](14)
其中α是任务A和任务B之间表示的可训练传递权重。我们证明了等式(14)中的Cross-stitch单元是以下命题的交叉压缩单元的简化版本:
命题3:如果我们忽略等式(2)中的所有偏差,交叉压缩单元可以写成:
[ v l + 1 e l + 1 ] = [ e l T w l V V v l T w l E V e l T w l V E v l T w l E E ] [ v l e l ] (15) \begin{bmatrix} v_{l+1} \\e_{l+1}\end{bmatrix} =\begin{bmatrix} e^T_lw_l^{VV} & v^T_lw_l^{EV}\\e^T_lw_l^{VE} & v^T_lw_l^{EE} \end{bmatrix}\begin{bmatrix} v_l \\ e_l \end{bmatrix} \tag{15} [vl+1el+1]=[elTwlVVelTwlVEvlTwlEVvlTwlEE][vlel](15)
等式(15)中的传递矩阵作为等式(14)中的Cross-stitch单元 [ α A A α A B ; α B A α B B ] [α_{AA} α_{AB};α_{BA}α_{BB}] [αAAαAB;αBAαBB]。像Cross-stitch网络一样,MKR网络可以通过将 v l ⊤ w l E V ( α A B ) v^⊤_l w^{EV}_l(α_{AB}) vl⊤wlEV(αAB)或 e l ⊤ w l V E ( α B A ) e^⊤_l w^{VE}_l(α_{BA}) el⊤wlVE(αBA)设置为零来决定使某些层特定于任务,或者通过分配较高的值来选择更共享的表示形式给他们。但由于交叉权重已从标量替换为两个矢量的点积,因此在交叉压缩单元中转移矩阵的粒度更细。注意到方程式相当有趣。等式(15)也可以被视为一种关注机制[1],因为转移权重的计算涉及特征向量 v l v_l vl和 e l e_l el本身。
4 实验
4.1数据集
我们在实验中利用了以下四个数据集:•MovieLens-1M是电影推荐中广泛使用的基准数据集,它由MovieLens网站上的大约100万个明确等级(范围从1到5)组成。
•Book-Crossing数据集包含Book-Crossing社区中的1,149,780本书的明确评分(从0到10)。
•Last.FM数据集包含来自Last.fm在线音乐系统的2000名用户的音乐家收听信息。
•Bing-News数据集包含从Bing News的服务器日志收集的从2016年10月16日至2017年8月11日期间的1,025,192条隐式反馈。每则新闻都有标题和摘要。
由于MovieLens-1M,Book-Crossing和Last.FM是显式反馈数据(Last.FM提供了听音计数作为每个用户-项目交互的权重),因此我们将它们转换为隐式反馈,其中每个条目都标有1,表示用户对该商品给予了正面评价,并为每个用户采样了一个标记为0的未监视商品。MovieLens1M的肯定评分阈值为4,而Book-Crossing和Last.FM由于稀疏而未设置阈值。我们使用Microsoft Satori为每个数据集构建KG,首先从整个KG中选择一个三元组的子集,其置信度大于0.9。对于MovieLens-1M和Book-Crossing,我们还从子KG中另外选择一个三元组子集,其子关系名称分别包含“电影”或“书”,以进一步减小KG的大小。给定子KG,对于MovieLens-1M,Book-Crossing和Last.FM,三元组分别为(head,film.film.name,tail),(head,book.book.title,tail)或(head,type.object.name,tail)。
为简单起见,排除了没有匹配或多个匹配实体的项目。然后,我们将ID与所有KG三元组的头部和尾部进行匹配,并从子KG中选择所有匹配良好的三元组。
Bing-News的构建过程类似,除了:(1)我们使用实体链接工具来提取新闻标题中的实体;(2)由于新闻标题中的实体不在一个特定域内,因此我们不对关系名称施加任何限制。表1中列出了这四个数据集的基本统计信息。请注意,由于我们过滤掉了KG中没有相应实体的项目,因此用户,项目和交互的数量比原始数据集要少。
4.2基准
我们将建议的MKR与以下基准进行比较。除非另有说明,否则基线的超参数设置与原始论文中所报告的相同或在其代码中作为默认设置。
•PER [39]将KG视为异构信息网络,并提取基于元路径的特征来表示用户和项目之间的连通性。在本文中,我们使用手动设计的用户项-属性-项路径作为功能,即MovieLens20M的“用户电影导演导演电影”,“用户电影原版电影”和“用户电影明星电影”;用于书阅览的“用户书作者书”和“用户书类型书”; “用户音乐人类型的音乐人”,“用户音乐人国家的音乐人”和“用户音乐人的年龄音乐人”(年龄离散)为Last.FM。请注意,PER不能应用于新闻推荐,因为很难为新闻中的实体预先定义元路径。
•CKE [40]在一个统一的建议框架中将CF与结构,文本和视觉知识相结合。
本文将CKE作为CF加结构知识模块来实现。四个数据集的用户和项目嵌入的维数分别设置为64、128、32、64。实体嵌入的尺寸为32。
•DKN [32]将实体嵌入和词嵌入视为多个通道,并将它们组合在一起在CNN中进行CTR预测。在本文中,我们使用电影/书名和新闻标题作为DKN的文本输入。单词嵌入和实体嵌入的维数为64,每个窗口大小1、2、3的过滤器数为128。
•RippleNet [31]是一种类似于内存网络的方法,可在知识图上传播用户的偏好以进行推荐。Last.FM的超参数设置为d = 8,H = 2,λ1= 10-6,λ2= 0.01,η= 0.02。
•LibFM [23]是一种广泛使用的基于特征的分解模型。我们将用户和项目的原始特征以及从TransR [13]中学到的相应平均实体嵌入进行串联,作为LibFM的输入。维度为{1,1,8},训练时期数为50。TransR的维度为32。
•Wide&Deep [3]是结合了(宽)线性通道和(深)非线性通道的深度推荐模型。Wide&Deep的输入与LibFM中的相同。用户,项目和实体的维度为64,我们使用两层深度为100和50的深层通道以及宽通道。
4.3实验设置
在MKR中,我们为所有三个数据集设置高级层数K = 1, f R S f_{RS} fRS作为内积,并且 λ 2 = 1 0 − 6 λ_2= 10^{-6} λ2=10−6,其他超参数在表1中给出。超参数的设置通过在验证集上优化AUC来确定。对于每个数据集,训练,验证和测试集的比率为6:2:2。每个实验重复3次,并报告平均性能。我们在两个实验场景中评估我们的方法:(1)在点击率(CTR)预测中,我们将训练后的模型应用于测试集中的每个互动,并输出预测的点击概率。我们使用AUC和准确性来评估点击率预测的效果。 (2)在前K个推荐中,我们使用经过训练的模型为测试集中的每个用户选择K个预测点击概率最高的项目,然后选择Precision @ K和Recall @ K评估推荐的集合。
4.4 实证研究
我们进行了一项经验研究,以研究RS中项目与KG中相应实体的相关性。具体而言,我们旨在揭示KG中项目对的公共邻居数如何随RS中公共评分者数的变化而变化。为此,我们首先从MovieLens-1M中随机抽取一百万个项目对,然后根据其在RS中的常见评分者数量将其分为5类,并计算每个类别在KG中其常见邻居的平均数量。结果显示在图2a中,该图清楚地表明,如果两项在RS中具有更常见的评估者,则它们很可能在KG中共享更多的共同邻居。图2b从相反方向显示了正相关。以上发现从经验上证明了项目在KG和RS中具有相似的相似度结构,因此项目的交叉知识转移对MKR中的推荐任务和KGE任务均有利。
4.5 结果
4.5.1与基准的比较
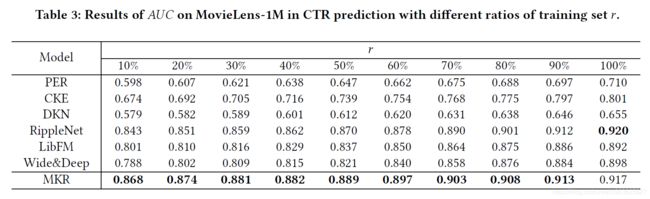

表2和图3、4分别显示了CTR预测和top-K推荐中所有方法的结果。
我们有以下观察结果:
•PER在电影,书籍和音乐推荐方面表现不佳,因为用户定义的元路径实际上很难达到最佳。此外,PER不能应用于新闻推荐。
•CKE在电影,书籍和音乐推荐方面的表现要优于新闻。这可能是因为MovieLens-1M,BookCrossing和Last.FM比Bing-News更为密集,这对于CKE中的协作过滤部分更有利。
•DKN与其他基准相比,在新闻推荐方面表现最佳,但在其他情况下表现最差。
这是因为电影,书籍和音乐家的名字太短且模棱两可,无法提供有用的信息。
•RippleNet在所有基准中表现最佳,甚至在MovieLens-1M上也胜过MKR。
这表明RippleNet可以精确地捕获用户兴趣,尤其是在用户与项目交互密集的情况下。但是,RippleNet对数据集的密度更敏感,因为它在Book-Crossing,Last.FM和Bing-News中的表现比MKR差。我们将在
4.5.3节中进一步研究它们在稀疏场景中的性能。
•MKR:一般情况下,我们的MKR在四个数据集的所有方法中表现最佳。
具体而言,MKR在电影,书籍,音乐和新闻推荐方面的平均准确率分别提高了11.6%,11.5%,12.7%和8.7%,这证明了MKR中多任务学习框架的功效。请注意,BingNews的前K个指标要低得多,因为新闻的数量明显大于电影,书籍和音乐家。
4.5.2与MKR变体的比较
我们进一步比较了MKR及其三个变体,以证明交叉压缩单元的功效:
•MKR-1L是具有一层交叉压缩单元的MKR,它对应于命题1的FM模型。请注意,在MovieLens-1M的实验中,MKR-1L实际上是MKR。
•MKR-DCN是基于等式(13)的MKR的变体,它对应于DCN模型。
•MKR-stitch是与Cross-stitch网络相对应的MKR的另一种变体,其中转移权重表示在等式(15)中被四个可训练标量代替。
从表2中,我们观察到MKR优于MKR-1L和MKR-DCN,这表明对项目和实体要素之间的高阶交互进行建模有助于保持良好的性能。MKR的得分也比MKR-stitch更好。与简单的cross-stitch单元相比,这证实了对MKR中的知识转移进行细粒度控制的功效。
4.5.3稀疏方案中的结果
在MKR中使用知识图的一个主要目标是减轻推荐系统的稀疏性和冷启动问题。
为了研究KGE模块在稀疏场景中的功效,我们将MovieLens-1M训练集的比例从100%更改为10%(同时将验证和测试集保持固定),并在CTR预测中报告AUC的结果 对于所有方法。结果显示在表3中。我们观察到,随着训练集的减少,所有方法的性能都会下降。当r = 10%时,与充满时相比,PER,CKE,DKN,RippleNet,LibFM和Wide&Deep的AUC得分分别下降15.8%,15.9%,11.6%,8.4%,10.2%,12.2%。使用训练集(r = 100%)。
相反,MKR的AUC分数仅降低5.3%,这表明即使用户-物品交互很少,MKR仍然可以保持良好的性能。我们还注意到,在稀疏场景中,MKR的性能优于RippleNet,这与我们在4.5.1节中的观察一致,即RippleNet对用户-物品交互的密度更为敏感。
4.6 参数敏感性
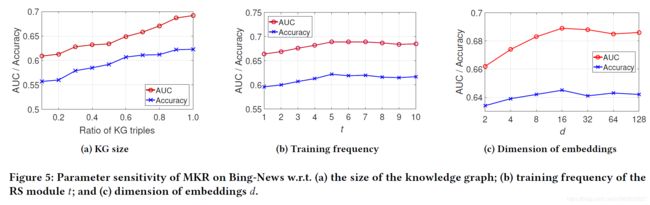
4.6.1 KG尺寸的影响
我们改变KG的大小以进一步研究KG的使用效果。Bing-News上的AUC结果如图5a所示。具体而言,在三种情况下,KG的比率从0.1分别提高到1.0和1.0,AUC和Accuracy分别提高了13.6%和11.8%。这是因为Bing-News数据集非常稀疏,使得KG使用的影响相当明显。
4.6.2 RS训练频率的影响
我们通过将t从1更改为10来调查Mt中参数t的影响,同时保持其他参数不变。结果显示在图5b中。我们观察到,当t = 5时,MKR达到最佳性能。这是因为KGE模块的高训练频率会误导MKR的目标函数,而KGE的训练频率太小则无法充分利用从KG。
4.6.3嵌入尺寸的影响
我们还将在图5c中显示用户,项目和实体的维度如何影响MKR的性能。我们发现,随着尺寸的增加,性能最初得到了改善,因为嵌入层中的更多位可以编码更多有用的信息。但是,当维数进一步增加时,性能会下降,因为维数过多可能会引入噪声,从而误导了后续的预测。
5 相关工作
5.1 知识图谱嵌入
MKR中的KGE模块连接到KGE方法中的大量工作。KGE用于将知识中的实体和关系嵌入到低维向量空间中,同时仍保留结构信息[33]。KGE方法可分为以下两类:(1)当学习实体和关系的表示形式(例如TransE [2],TransH [35]和TransR [13])时,转换距离模型会利用基于距离的评分功能; (2)语义匹配模型通过匹配实体和关系的潜在语义(例如RESCAL [20],ANALOGY [19]和HolE [14])来衡量知识三元组的合理性。最近,研究人员还提议合并辅助信息,例如实体类型[36],逻辑规则[24]和文本描述[46]以帮助KGE。
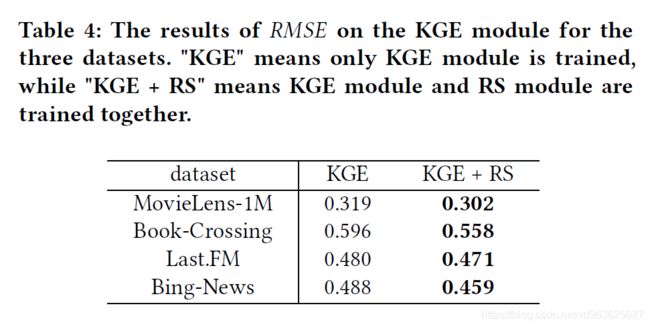
上面的KGE方法也可以作为KGE模块的实现并入MKR,但是请注意,MKR中的交叉和压缩单元需要相应地重新设计。探索KGE模块的其他设计以及相应的桥接单元也是未来工作的重要方向。
5.2 多任务学习
多任务学习是机器学习中的一种学习范式,其目的是利用包含在多个相关任务中的有用信息来帮助提高所有任务的泛化性能[42]。假定所有学习任务都相互学习,发现与单独学习它们相比,共同学习这些任务可以提高性能。通常,MTL算法可以分为几类,包括特征学习方法[34、41],低等级方法[7、16],任务聚类方法[47],任务关系学习方法[12]和分解方法 [6]。例如,Cross-stitch网络[41]通过知识转移矩阵确定不同任务中隐藏层的输入; [47]旨在通过识别代表任务(它们是给定的m个任务的子集)来对任务进行聚类,即,如果任务Tj选择任务Ti作为代表任务,则可以预期Tj的模型参数与那些相似。MTL还可以与其他学习范例结合使用,以进一步提高学习任务的性能,包括半监督学习,主动学习,无监督学习和强化学习。
我们的工作可以看作是一个非对称的多任务学习框架[37、43、44],我们的目标是利用RS和KG之间的联系来帮助提高其性能,并且以不同的频率训练这两项任务。
5.3深度推荐系统
近年来,深度学习已使推荐器系统发生了革命性变化,并在许多推荐方案中获得了更好的性能。粗略地说,深度推荐系统可以分为两类:
(1)使用深度神经网络处理用户或项目的原始特征[5、28-30、40]; 例如,协作深度学习[29]设计了自动编码器,以从文本输入中提取简短和密集的特征,并将特征馈入协作过滤模块; DeepFM [5]在神经网络架构中结合了用于推荐的分解机器和用于特征学习的深度学习。
(2)使用深度神经网络来建模用户与项目之间的交互[3、4、8、9]。例如,神经协作过滤[8]用神经体系结构代替了内部产品,以对用户-项目交互进行建模。这些方法与我们的方法之间的主要区别在于,MKR部署了一个多任务学习框架,该框架利用KG的知识来辅助推荐。
6 结论和未来工作
本文提出了MKR,一种用于知识图增强推荐的多任务学习方法。MKR是一个深层的端到端框架,由两部分组成:推荐模块和KGE模块。这两个模块均采用多个非线性层,以从输入中提取潜在特征,并适应用户项和头部关系对的复杂交互。由于这两个任务不是独立的,而是由项目和实体连接的,因此我们在MKR中设计了一个交叉压缩单元来关联这两个任务,它可以自动学习项目和实体特征的高级交互,并在这两个任务之间传递知识。我们在四个推荐方案中进行了广泛的实验。结果表明,MKR优于强基线,并具有使用KG的功效。为了将来的工作,我们计划在MKR框架中研究其他类型的神经网络(例如CNN)。通过重新设计交叉压缩单元,我们还将其他KGE方法作为MKR中的KGE模块实现。