吴恩达机器学习第二次作业(python实现):逻辑回归
逻辑回归
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as opt
from sklearn.metrics import classification_report
import pandas as pd
from sklearn import linear_model
# 获取原始数据
def raw_data(path):
data=pd.read_csv(path,names=['exam1','exam2','admit'])
return data
# 绘制原始数据
def draw_data(data):
accept=data[data['admit'].isin([1])]
refuse=data[data['admit'].isin([0])]
plt.scatter(accept['exam1'],accept['exam2'],c='g',label='admit')
plt.scatter(refuse['exam1'],refuse['exam2'],c='r',label='not admit')
plt.title('admission')
plt.xlabel('score1')
plt.ylabel('score2')
return plt
# sigmoid函数
def sigmoid(z):
return 1/(1+np.exp(-z))
# 代价函数
def cost_function(theta,x,y):
m=x.shape[0]
j=(y.dot(np.log(sigmoid(x.dot(theta))))+(1-y).dot(np.log(1-sigmoid(x.dot(theta)))))/(-m)
return j
# 计算偏导数即可
def gradient_descent(theta,x,y):
return ((sigmoid(x.dot(theta))-y).T).dot(x)
# 假设函数
def predict(theta,x):
h=sigmoid(x.dot(theta))
return [1 if x>=0.5 else 0 for x in h]
# 决策边界theta*x=0
def boundary(theta,data):
x1=np.arange(20,100,0.01)
x2=(theta[0]+theta[1]*x1)/-theta[2]
plt=draw_data(data)
plt.title('boundary')
plt.plot(x1,x2)
plt.show()
def main():
data=raw_data('venv/lib/dataset/ex2data1.txt')
# print(data.head())
# plt=draw_data(data)
# plt.show()
x1=data['exam1']
x2=data['exam2']
x=np.c_[np.ones(x1.shape[0]),x1,x2]
y=data['admit']
# 不要将theta初始化为1,初始化为1的话,h(x)会过大,sigmoid近似返回1,log(1-h(x))无意义
theta=np.zeros(x.shape[1])
# print(cost_function(theta,x,y)) # 0.6931471805599453
# theta=opt.fmin_tnc(func=cost_function,x0=theta,fprime=gradient_descent,args=(x,y))
theta=opt.minimize(fun=cost_function,x0=theta,args=(x,y),method='tnc',jac=gradient_descent)
theta=theta.x
# print(cost_function(theta,x,y))
print(classification_report(predict(theta,x),y))
'''
model=linear_model.LogisticRegression()
model.fit(x,y)
print(model.score(x,y))
'''
boundary(theta,data)
main()
关于opt.fmin_tnc()函数的参数问题
func是要最小化的函数
x0是最小化函数的自变量
fprime是最小化的方法
args是func的除theta外的
opt.minimize()函数的参数基本同上
结果:
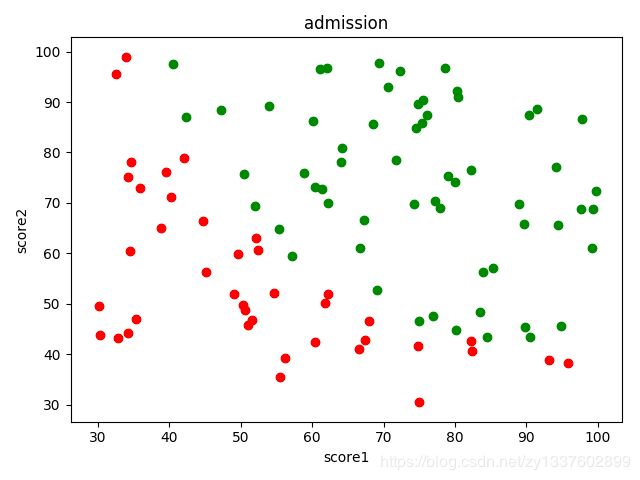
训练数据集
决策边界

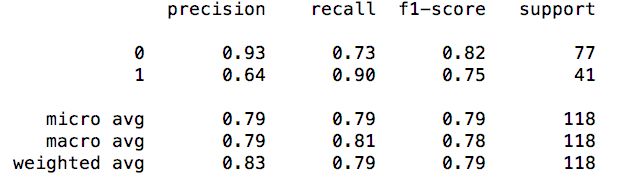
classification_report()的结果:
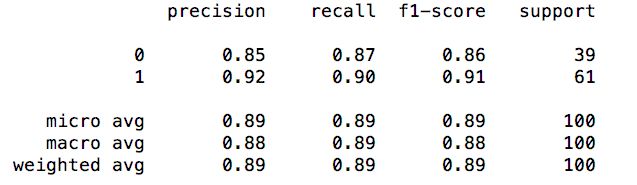
关于如何看classification_report()的结果,请看classification_report结果说明
正则化逻辑回归
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
import scipy.optimize as opt
from sklearn.metrics import classification_report
# 读取数据
def raw_data(path):
data=pd.read_csv(path,names=['test1','test2','accept'])
return data
# 画出原始数据
def draw_data(data):
accept=data[data['accept'].isin(['1'])]
reject=data[data['accept'].isin(['0'])]
plt.scatter(accept['test1'],accept['test2'],c='g')
plt.scatter(reject['test1'],reject['test2'],c='r')
plt.title('raw_data')
plt.xlabel('test1')
plt.ylabel('test2')
return plt
# 特征映射
def feature_mapping(x1,x2,power):
datamap={}
for i in range(power+1):
for j in range(i+1):
datamap["f{}{}".format(j,i-j)]=np.power(x1,j)*np.power(x2,i-j)
return pd.DataFrame(datamap)
def sigmoid(z):
return 1/(1+np.exp(-z))
# 正则化代价函数
def regularized_cost_function(theta,x,y,lam):
m=x.shape[0]
j=((y.dot(np.log(sigmoid(x.dot(theta)))))+((1-y).dot(np.log(1-sigmoid(x.dot(theta))))))/-m
penalty=lam*(theta.dot(theta))/(2*m)
return j+penalty
# 计算偏导数
def regularized_gradient_descent(theta,x,y,lam):
m=x.shape[0]
partial_j=((sigmoid(x.dot(theta))-y).T).dot(x)/m
partial_penalty=lam*theta/m
# 不惩罚第一项
partial_penalty[0]=0
return partial_j+partial_penalty
def predict(theta,x):
h=x.dot(theta)
return [1 if x>=0.5 else 0 for x in h]
def boundary(theta,data):
"""
[X,Y] = meshgrid(x,y)
将向量x和y定义的区域转换成矩阵X和Y,
其中矩阵X的行向量是向量x的简单复制,而矩阵Y的列向量是向量y的简单复制
假设x是长度为m的向量,y是长度为n的向量,则最终生成的矩阵X和Y的维度都是 nm(注意不是mn)
"""
# 绘制方程theta*x=0
x = np.linspace(-1, 1.5, 200)
x1, x2 = np.meshgrid(x, x)
z = feature_mapping(x1.ravel(), x2.ravel(), 6).values
z = z.dot(theta)
# print(xx.shape) # (200,200)
# print(z.shape) # (40000,)
z=z.reshape(x1.shape)
plt=draw_data(data)
plt.contour(x1,x2,z,0)
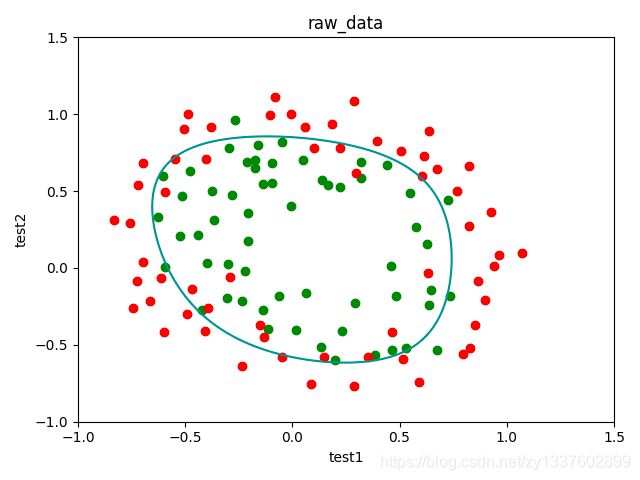
plt.title('boundary')
plt.show()
def main():
rawdata=raw_data('venv/lib/dataset/ex2data2.txt')
# print(rawdata.head())
# plt=draw_data(rawdata)
# plt.show()
data=feature_mapping(rawdata['test1'],rawdata['test2'],power=6)
# print(data.head())
x=data.values
y=rawdata['accept']
theta=np.zeros(x.shape[1])
'''
print(type(x))
print(type(y))
print(type(data))
print(x.shape)
print(y.shape)
print(theta.shape)
'''
# print(regularized_cost_function(theta,x,y,1)) #0.6931471805599454
theta=opt.minimize(fun=regularized_cost_function,x0=theta,args=(x,y,1),method='tnc',jac=regularized_gradient_descent).x
# print(regularized_cost_function(theta,x,y,1)) # 0.5357749513533407
# print(classification_report(predict(theta,x),y))
boundary(theta,rawdata)
main()