【人工智能】人工智能课程复习笔记
第2章 知识表示方法
一阶谓语逻辑表示法、产生式表示法、语义网络表示法、框架表示法、面向对象表示法、状态空间表示法。
一阶谓语逻辑表示法
连接词:~ 非、∧与合取、∨或析取、→条件、↔双条件
量词:存在 与 任意
![]()
![]()
举例谓语公式表示知识:
HIGHER (x, y):x比y长得高
产生式表示法
P前提→Q结论 或者 IF P THEN Q
例:“老李年龄是40岁”,可表示为:(Li,Age,40)
例:“老李年龄很可能是40岁”,可表示为: (Li,Age,40,0.8)
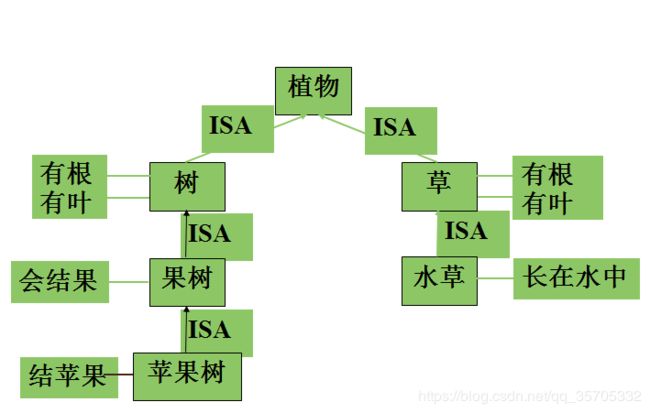
语义网络表示法
是通过概念及语义关系表达的一种网络图,带标注的有向图。
常用语义连续:ISA/AKO(是一个),part_of,IS,compose_of,have,located,if-then,before,after,at,a-member-of
框架表示法
例 教师框架
解:框架名:<教师>
姓名:单位(姓、名)
年龄:单位(岁)
性别:范围(男、女)
缺省:男
职称:范围(教授、副教授、讲师、助教)
缺省:讲师
部门:单位(学院、教研室)
住址:<住址框架>
工资:<工资框架>
参加工作时间:单位(年,月)
面向对象表示法
对象:人
类:鸡、飞禽、动物类在概念上是一种抽象机制,它是对一组相似对象的抽象。
继承....
状态空间表示法
第3章 归结推理方法
命题、命题公式
=1 谓语公式的永真性和可满足性
谓词公式的等价性 化简常用公式 狄摩根定律与量词转换率非常常用!
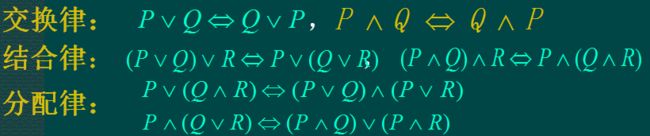

=2 置换与合一
1 置换
{a/x,f(b)/y,w/z}表示为 x=a;y=f(b),z=w
2合一
例1:L1=Q(a,y),L2=Q(z,f(b))
它们是可以合一的,其合一置换为S={a/z,f(b)/y},并且S也是最一般合一者mgu。
=3归结推理
1范式:
前束形范式:不出现连接词→和 ↔
斯克林(sklolem)范式:将前束范式每个存在量词均在全称量词的前面
斯克林标准型:从前束型范式中消去全部存在量词
合取范式:(A∨B)∧(A∨C)就是一个合取范式
2子句与子句集:谓词公式G的Skolem标准型前面的全称量词全部消去,并用逗号(,)代替合取符号∧,便可得到谓词公式G的子句集S
3归结原理
互补文字(P与~P为互补文字)
=4归结原理进行定理证明
对于定理证明,常见的形式是:A1∧A2∧……∧An→B其中,A1∧A2∧……∧An是前提条件,而B则是逻辑结论。 要证明B是A1∧A2∧……∧An的逻辑结论,只需证明:A1∧A2∧……∧An∧~B 是不可满足的即可。
证明过程:
Step1.首先否定结论B,并将否定后的公式~B与前提公式集组成如下形式的谓词公式:
G= A1∧A2∧……∧An∧~B
Step2.求谓词公式G的子句集S。 (化简为斯克林标准形式)
Step3.应用归结(消解)原理,互补消去
消去到最后,为空集NIL;
=5归结原理进行问题求解
求解过程
Step1.把已知前提条件用谓词公式表示出来,并化成相应的子句集,设该子句集的名字为S1;
Step2.把待求解的问题也用谓词公式表示出来,然后将其否定,并与一谓词ANSWER构成析取式。谓词ANSWER是一个专为求解问题而设置的谓词,其变量必须与问题公式的变量完全一致。
Step3.把问题公式与谓词ANSWER构成的析取式(或)化为子句集,并把该子句集与S1合并构成子句集S。
Step4.对子句集S应用消解原理进行消解,在消解过程汇总,通过合一置换,改变ANSWER中的变量。
Step5.如果得到消解式ANSWER,则问题的答案即在ANSWER谓词中。
=6归结原理的控制策略
第4章 不确定推理法
=1不确定推理
分类:模型法(数值方法、非数值方法)、控制方法
基于概率论的基础处理不确定性的方法:可信度方法、主观bayes方 法。
=2可信度方法
1知识不确定性
知识的不确定性则是以可信度CF(H,E)表示的。其一般形式为IF E THEN H (CF(H,E) )
2证据不确定性的表示
例如CF(E)=0.8表示证据E的可信度为0.8。
3不确定性的推理计算
=3主观bayes法
1知识不确定性
2证据不确定性的表示
3不确定性的推理计算
4结论不确定性合成算法
=4证据理论
证据理论的数学基础
特定概率分配函数
第5章 状态空间搜索策略
盲目搜索策略
1宽度优先搜索:
宽度优先搜索是一般图搜索算法的一个实例,每次总是扩展深度最浅的节点,这可以通过将边缘组织成FIFO队列来实现(即,新节点加入到队列尾,浅层的老节点会在深层节点之前被扩展)。
2深度优先:
深度优先总是扩展搜索树的当前边缘节点集 中最深的节点(搜索直接推到最深层)。如果最深层节点扩展完了,就回溯到下一个还有未扩展节点的深度稍浅的节点。DFS使用LIFO队列(最新生成的节点最早被扩展)。
3一致代价搜索
一致代价搜索扩展的是路径消耗g(n)(从初始状态到当前状态的路径耗散)最小的节点n。(可以通过将边缘节点组织成按g值排序的队列来实现)
4 深度受限
设置界限l来避免DFS在无限状态空间下搜索失败的尴尬情况。即,深度为l的节点被当做最深层节点(没有后继节点)来对待。
后面包括了浅谈深度学习,机器学习 因为在其他课程有所涉及也就不一一列出来了