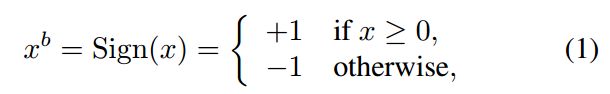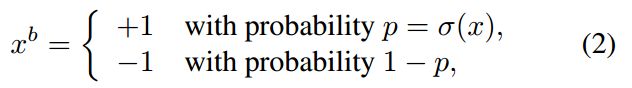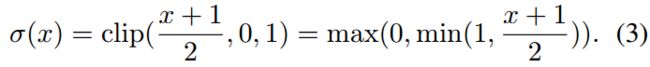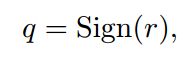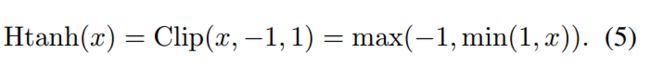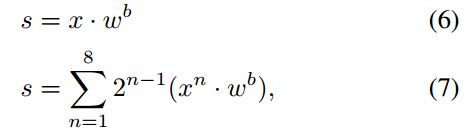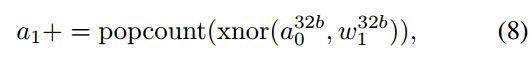二值化网络：BNN 论文阅读笔记

论文：《Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or -1》

连接：https://arxiv.org/pdf/1602.02830.pdf

 

摘要

    我们介绍了一种训练二进制神经网络（BNN）的方法-在运行时，神经网络具有二进制权重和激活值。 在训练时，使用二进制权重和激活来计算参数梯度。 在前向传递过程中，BNN大大减少了内存大小和访问，并用按位运算代替了大多数算术运算，这有望显着提高功率效率。 为了验证BNN的有效性，我们在Torch7和Theano框架上进行了两组实验。 在这两个方面，BNN在MNIST，CIFAR-10和SVHN数据集上取得了近乎state-of-the-art的结果。 最后但并非最不重要的一点是，我们编写了一个二进制矩阵乘法GPU 内核，通过该内核，我们的MNIST BNN可以比未优化的GPU 内核快7倍运行，而不会损失任何分类精度。 训练和运行BNN代码已经开源。

引言

    深度神经网络（DNN）在很多任务上都大大推动了人工智能（AI）的局限性，包括但不限于从图像中识别目标，语音识别，统计机器翻译，Atari和Go游戏，甚至抽象艺术。

    如今，DNN几乎只接受一个或多个非常快速且耗电的图形处理单元（GPU）的训练。 结果，在目标低功率设备上运行DNN通常是一个挑战，并且投入了大量的研究工作来在运行时在两种通用目标和专用计算机硬件上加速DNN。

本文的贡献如下：
    •我们介绍了一种训练二值化神经网络（BNN）的方法，BNN在运行时（推理阶段）具有二进制权重和激活值，并在训练时计算参数梯度（请参见第1节）。
    •我们进行了两组实验，每组实验都在不同的框架上实施，分别是Torch7和Theano，这表明有可能 在MNIST，CIFAR-10和SVHN上训练BNN，并获得近乎start-of-the-art的结果（请参阅第2节）。
    我们表明，在前向传播（运行时和训练时）中，BNN大大减少了内存消耗（大小和访问次数），并用按位运算代替了大多数有可能导致功率效率显着增加的算术运算（请参阅第3节）。 而且，二值化的CNN可以导致二进制卷积核的重复利用。 我们认为专用硬件可以将时间复杂度降低60％。
    •最后但并非最不重要的一点是，我们对二进制矩阵乘法GPU 内核进行了编程，使用它可以使MNIST BNN的运行速度比未经优化的GPU 内核快7倍，而不会损失分类精度（请参见第4节）。
    •用于训练和运行我们的BNN的代码可以在线获得（在Theano框架1和Torch框架2中）

1.二值化神经网络

    在本节中，我们将详细介绍二值化函数，展示如何使用它来计算参数梯度，以及如何通过它进行反向传播。

1.1 确定性与随机二值化

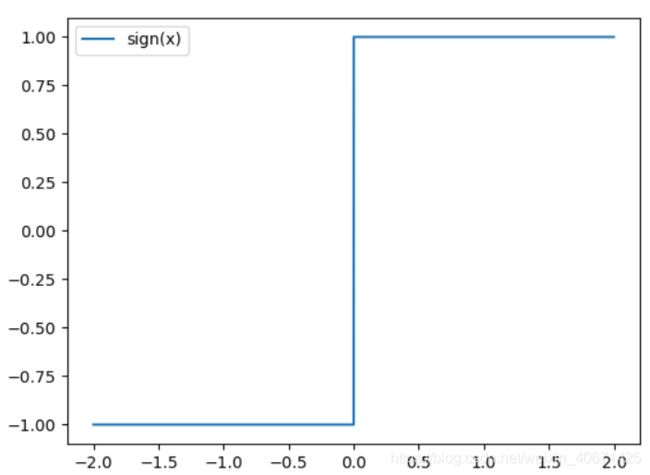
    在训练BNN时，我们将权重和激活值都限制为+1或-1。 从硬件角度来看，这两个值非常有优势，正如我们在第4节中所述。为了将实值变量转换为这两个值，我们使用了两个不同的二值化函数，如（Courbariaux et al。，2015）。 我们的第一个二值化函数是确定性的：（符号函数）

    其中是二值化变量（权重或激活值），x是实数值变量。 它非常容易实现，并且在实践中效果很好。 我们的第二个二值化函数是随机的：

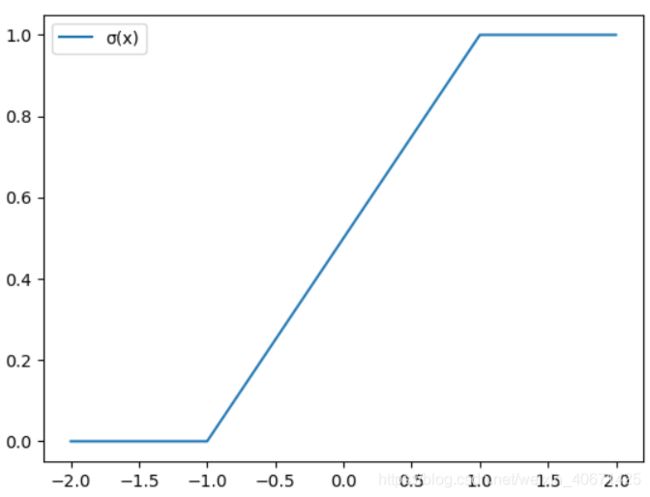
    其中σ是“hard sigmoid”函数：

    随机二值化比符号函数更具吸引力，但难以实现，因为它要求硬件在量化时生成随机位。 结果，除了在某些实验中在训练时激活值外，我们大多使用确定性二值化函数（即符号函数）。

1.2 梯度计算与累积

    尽管我们的BNN训练方法使用二进制权重和激活值来计算参数梯度，但是权重的实际值梯度会根据算法1累积在实际值变量中。随机梯度下降（SGD）可能需要实际值权重来工作。 SGD会以较小且具有噪声的步长探索参数的空间，并通过每个权重中积累的随机梯度贡献来平均噪声。 因此，重要的是要为这些累加器保持足够的分辨率，乍一看表明绝对需要高精度。

 

    而且，在计算参数梯度时，在权重和激活上添加噪声会提供一种形式化的正则化形式，有助于更好地泛化，如先前使用变分法，权重噪声，Dropout和DropConnect 所示。 我们训练BNN的方法可以看作是Dropout的一种变体，在计算参数梯度时，我们将激活值和权重二值化，而不是将激活函数的一半随机设置为零。

1.3 通过离散化传播梯度

    符号函数导数几乎在任何地方都为零，这显然与反向传播不兼容，因为相对于离散化之前，提取量化梯度的成本（预激活或权重）为零。 请注意，即使使用随机量化，也是如此。 Bengio（2013）研究了通过随机离散神经元估计或传播梯度的问题。 他们在实验中发现，使用先前在Hinton（2012）的演讲中介绍的“直通估算器”可获得最快的训练。

    我们采用类似的方法，但是使用了直通估计器的版本，该版本考虑了饱和效应，并且确实使用了确定性而非随机采样的bit。 考虑符号函数量化：

    并假设已经获得了梯度的估计量（需要时使用直通式估计量）。 然后，我们的直接估计量就是
：

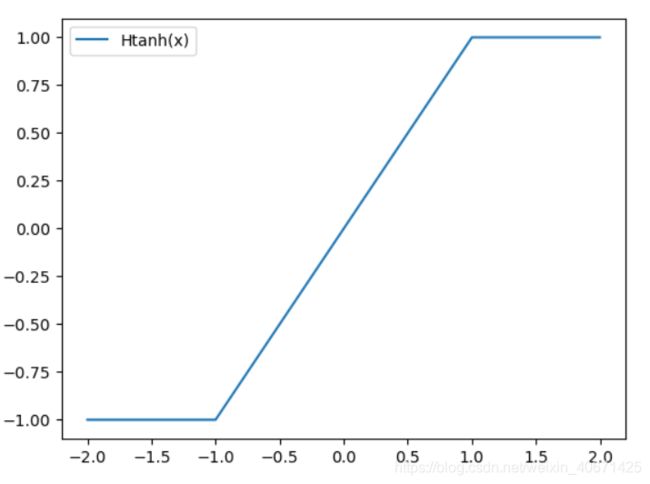
    请注意，这会保留梯度的信息，并在 r 太大时取消梯度。 当 r 太大时不取消梯度会明显降低性能。 算法1说明了这种直通估算器的用法。导数 也可以看作是通hard tanh传播梯度，它是以下分段线性激活函数：

    对于隐藏单元，我们使用符号函数非线性来获取二进制激活值，对于权重，我们结合了两种方法：
    •当权重更新使  在[−1，1]之外时，通过将映射为-1或1，将每个实值权重限制在-1和1之间。即按照算法1在训练过程中裁剪权重。否则，实值权重会变得非常大，而对二进制权重没有任何效果。
    •使用权重  时，使用对其进行量化。

    根据等式4，这与  时的梯度消除相一致。

    算法1训练BNN。 C是mini-batch的代价函数，λ-学习率衰减因子，L是层数。 ◦ 表示逐元素乘法。 Binarize()函数指定如何（随机或确定性）对激活和权重进行二值化，以及Clip()如何限制权重。 BatchNorm()指定如何使用Batch Normalize（Ioffe＆Szegedy，2015）是常用的batch normalize还是其在算法3中描述的基于移位的变体对激活值进行Batch Normalize。BackBatchNorm()指定如何通过归一化进行反向传播。 Update()指定使用ADAM优化器（Kingma＆Ba，2014）或我们在算法4中描述的基于位移的AdaMax来在已知其梯度时如何更新参数。

    算法2：基于移位的Batch Normailze变换，在一个mini-batch上激活 x。 是2的近似幂，并且<<>>代表左右二进制移位。（激活函数前）

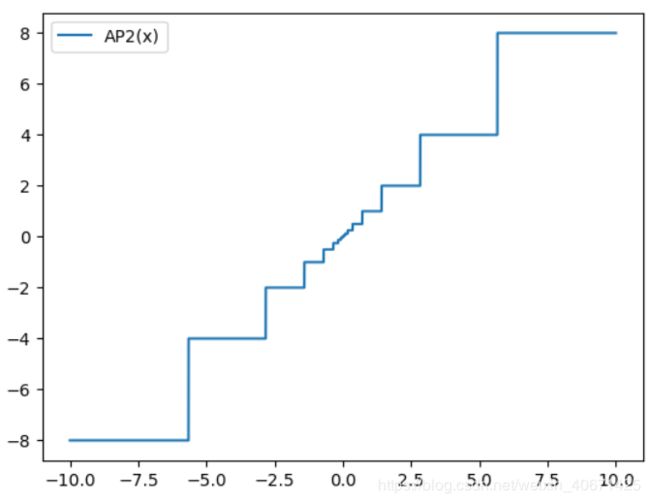
    算法3： 基于移位的Batch Normalize变换，应用于mini-batch上处理 activation(x)。 其中AP2是2的幂的近似，而<< >>代表左右二进制移位。（激活函数后）

    算法4： 基于移位的AdaMax学习规则（Kingma＆Ba，2014）。  表示元素的平方  。 好的默认设置为。 向量上的所有操作都是按元素进行的。 对于和，我们将和表示为幂  t。  

1.4 基于Shift的Batch Normalization

    Batch Normalization（BN）（Ioffe和Szegedy，2015年），不仅可以加快训练速度，而且还可以减轻权重尺度的整体影响。normalization噪声也可能有助于对模型进行正则化。但是，在训练时，BN需要进行许多乘法运算（计算标准差并除以标准差），即除以运行方差（训练集激活方差的加权平均值）。尽管缩放计算的次数与神经元的数目相同，但对于ConvNets，此数目非常大。例如，在CIFAR-10数据集（使用我们的结构）中，仅由128×3×3 filter mask组成的第一卷积层将尺寸为3×32×32的图像转换为尺寸为3×128×28×28的图像，比权重的数量大两个数量级。为了获得BN可获得的结果，我们使用基于移位的batch normalization（SBN）技术。在算法3中有详细介绍。SBN几乎没有乘法就近似BN。在我们进行的实验中，当使用基于位移的BN算法而不是vanilla BN算法时，我们没有观察到精度损失。

1.5 . Shift based AdaMax

    ADAM学习规则（Kingma和Ba，2014年）似乎也减轻了权重缩放（weight scale）的影响。 由于ADAM需要许多乘法运算，因此我们建议改用我们在算法4中详细介绍的基于位移的AdaMax。在实验中，我们进行了实验，在使用基于位移的AdaMax算法而不是原始的ADAM算法时，没有观察到精度损失。

1.6 第一层

    在BNN中，在所有计算中仅使用权重和激活的二值化值。 由于当前层的输出是下一层的输入，因此除第一层外，所有层的输入均为二进制（相当于特征二值化）。 但是，我们认为这不是主要问题。 首先，在计算机视觉中，输入表示通常比内部表示通常（例如512）具有更少的通道（例如，红色，绿色和蓝色）。 结果，就参数和计算而言，ConvNet的第一层通常是最小的卷积层（Szegedy等，2014）。

    其次，以m位精度将连续值输入处理为定点数来处理相对容易。 例如，在8位定点输入的常见情况下：

    其中 x 是1024个8位输入的向量，是第一个输入的最高有效位，是1024个1-bit权重的向量，而 s 是结果加权和。 该trick在算法5中使用。

2.基准结果

    我们进行了两组实验，每组实验都基于不同的框架，即Torch7和Theano。 除了框架之外，两组实验非常相似：

    •在这两组实验中，我们都使用MNIST，CIFAR-10和SVHN基准数据集上的BNN获得了近乎start-of-the-art的结果。

    •在我们的Torch7实验中，激活是在训练时随机二值化的，而在我们的Theano实验中，确定性是二值化的。

    •在我们的Torch7实验中，我们使用基于移位的BN和AdaMax变体，在算法3和4中进行了详细介绍，而在Theano实验中，我们使用了 原始的BN和ADAM。

2.1 MNIST上的MLP（Theano）
MNIST是图像分类基准数据集（LeCun等，1998）。它由一个60K的训练集和一个10K的28×28灰度图像测试集组成，代表从0到9的数字。为了保持这一基准，我们没有使用任何卷积，数据增强，预处理或无监督学习。我们在MNIST上训练的MLP包含3个隐藏的层，其中4096个二进制单位（请参见第1节）和一个L2-SVM输出层。在多个分类基准上，L2-SVM的性能优于Softmax（Tang，2013； Lee等，2014）。我们使用Dropout规范化了模型（Srivastava，2013； Srivastava等，2014）。使用ADAM自适应学习率方法可以将平方hinge loss降到最低（Kingma＆Ba，2014）。根据算法1，我们使用呈指数衰减的全局学习率，并根据Courbariaux等人的建议，使用权重的初始化系数（来自（Glorot＆Bengio，2010））来缩放权重的学习率。 （2015）。我们将批量标准化使用大小为100的小批量来加快训练速度。通常，我们将训练集的最后10K个样本用作验证集，以进行早期停止和模型选择。我们报告了1000个epochs后与最佳验证错误率相关的测试错误率（我们不对验证集进行重新训练）。结果记录在表1中。

2.2 MNIST上的MLP（Torch7）

    我们使用与Theano实验中类似的体系结构，没有dropout，并且每层2048个二进制单元而不是4096。此外，我们使用基于移位的AdaMax和BN（最小批量为100）代替原始实现， 减少乘法次数。 同样，我们每10个epochs使用1-bit右移来降低学习率。 结果列于表1

2.3 CIFA-10上的ConvNet (Theano)

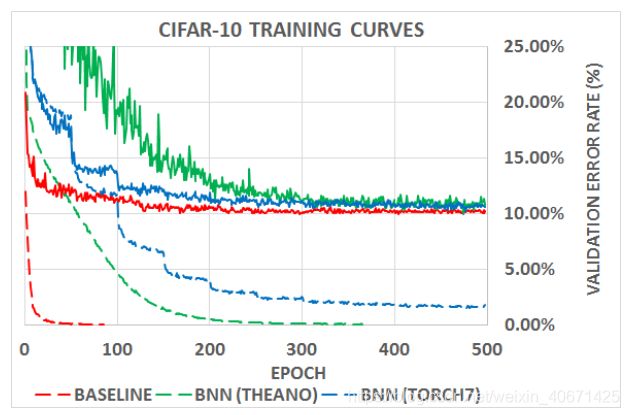
    CIFAR-10是图像分类基准数据集。它由一个大小为50K的训练集和一个大小为10K的测试集组成，其中实例是32×32彩色图像，分别代表飞机，汽车，鸟类，猫，鹿，狗，青蛙，马，船和卡车。我们不使用任何预处理或数据扩充（对于该数据集，这实际上可以改变游戏规则（Graham，2014））。除了激活的二值化，我们的ConvNet的体系结构与？的体系结构相同。 Courbariaux等。 Courbariaux et al.（2015）的结构本身主要受VGG的启发（Simonyan＆Zisserman，2015）。使用ADAM可以将平方hinge loss降至最低。就像MNIST一样，我们使用指数递减的学习速率。我们用权重的初始化系数来衡量权重的学习率（Glorot和Bengio，2010年）。我们使用mini-batch size最为50的batch normalization来加快训练速度。我们使用训练集的最后5000个样本作为验证集。在500个训练epochs后，我们报告与最佳验证错误率相关的测试错误率（我们不对验证集进行重新训练）。结果在表1和图1中给出。

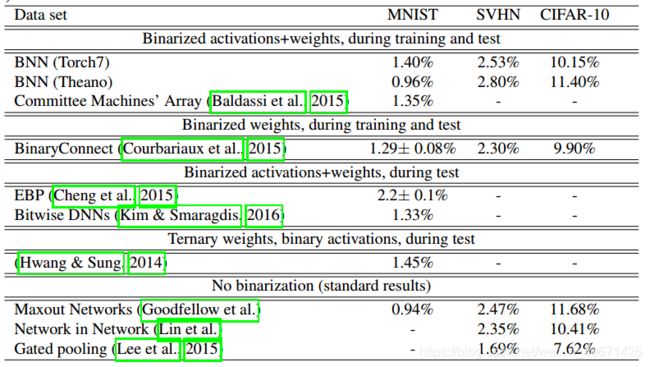
表1.在MNIST（没有无监督的预训练的MLP架构），CIFAR-10（无数据扩充）和SVHN上训练的DNN的分类测试错误率。

图1.在CIFAR-10上使用ConvNet的训练曲线。 虚线表示训练loss（平方 hinge loss），而虚线表示相应的验证错误率。 尽管BNN的训练速度较慢，但其准确性几乎与32位浮点DNN一样。

2.4 ConvNet上的CIFAR-10 (Torch7)

    我们使用与Theano实验相同的架构。我们使用基于移位的AdaMax和BN（mini-batch size为200）而不是原始实现来减少乘法次数。 同样，我们通过每50个epochs使用1-bit右移来降低学习率。 结果在表1和图1中给出。

2.5 ConvNet上的SVHN

    SVHN还是图像分类基准数据集。 它由大小为604K个样本训练集和大小为26K的测试集组成，其中实例为32×32彩色图像，表示从0到9的数字。在两组实验中，我们都采用与CIFAR- 10个实验，但有几个值得注意的例外：我们使用卷积层中单元数量的一半，并且训练200个epochs而不是500个epochs（因为SVHN比CIFAR-10大得多）。 结果在表1中给出。

3.向前传播时非常省电

    通用或专用的计算机硬件由内存，算术运算符和控制逻辑组成。 在正向传递过程中（在运行时和训练时），BNN都会大大减少内存大小和访问量，并用按位运算代替大多数算术运算，这可能会大大提高功率效率。 此外，二值化的CNN可以导致二进制卷积核重复，并且我们认为专用硬件可以将时间复杂度降低60％。

3.1 内存size和访问

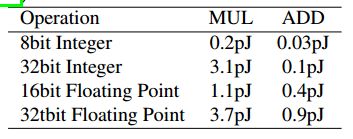
    提高计算性能一直是并且仍然是一个挑战。 在过去十年中，功率一直是性能的主要限制因素（Horowitz，2014年）。 这就是为什么许多研究工作致力于减少神经网络的能耗的原因。 Horowitz（2014）提供了计算能耗的粗略数字（给定的数字用于45nm技术），如表2和表3所示。重要的是，我们可以看到，内存访问通常比算术操作消耗更多的能源，而内存访问则消耗了更多能量。 内存大小会增加成本。 与32位DNN相比，BNN需要32倍小的内存大小和32倍更少的内存访问。 预计这将大大降低能耗（即超过32倍）

表2 乘加运算的能耗

表3 内存访问能耗

 

3.2 XNOR-Count

    应用DNN主要包括卷积和矩阵乘法。 因此，深度学习的关键算术运算是乘法和加法运算。 人工神经元基本上是乘法累加器，用于计算其输入的加权和。 在BNN中，激活和权重都被限制为-1或+1。 结果，大多数32位浮点乘法累加被1位XNOR计数操作代替。 这可能会对深度学习专用硬件产生重大影响。 例如，一个32位浮点乘法器的成本约为200 Xilinx FPGA Slice（Govindu等人，2004； Beauchamp等人，2006），而1位XNOR门仅需花费一个slice。

3.3 利用filter重复

    当使用具有二进制权重的ConvNet结构时，唯一filter的数量受filter大小的限制。例如，在我们的实现中，我们使用大小为3×3的filter，因此唯一2D filter的最大数量为2^9 =512。但是，这不应阻止将特征图的数量扩展到该数量之外，因为实际的filter是3D矩阵。假设在卷积层中有个filters，我们必须存储大小为的4D权重矩阵。因此，唯一filter器的数量为。必要时，我们在特征图上应用每个filter，并执行所需的乘法累加（MAC）操作（在我们的示例中，使用XNOR和popcount操作）。由于我们现在有了二进制filter，因此许多大小为k×k的2Dfilter会重复它们自己。通过使用专用的硬件/软件，我们只能在每个特征图上应用唯一的2D filter，并明智地将结果求和，以接收每个3D filter的卷积结果。注意，逆滤波器（即[-1,1，-1]是[1，-1,1]的逆）也可以视为重复；它只是原始滤波器乘以-1的乘积。例如，在经过CIFAR-10基准训练的ConvNet架构中，平均每层只有42％的唯一filter。因此，我们可以将XNORpopcount操作的数量减少3。

4. 运行时在GPU上快七倍

    通过使用有时被称为寄存器（SWAR）内的SIMD（单指令，多个数据）的方法，可以加快BNN的GPU实现。 SWAR的基本思想是将32个二进制变量的组连接到32位寄存器中，从而在按位运算（例如XNOR）上获得32倍的加速。 使用SWAR，仅需3条指令就可以评估32个连接：

    其中是结果加权和，而和是串联的输入和权重。 在最近的Nvidia GPU上，这3条指令（累加，popcount，xnor）占用1 + 4 + 1 = 6个时钟周期（如果它们成为融合指令，则只需一个时钟周期）。 因此，我们获得的Nvidia GPU理论上的加速比为32 / 6≈5.3。 实际上，由于存储器带宽与计算的比率也增加了6倍，因此这种加速非常容易实现。

    为了验证这些理论结果，我们编写了两个GPU内核：
    •第一个内核（基准）是一个未经优化的矩阵乘法内核。
    •第二个内核（XNOR）与基线内核几乎相同，不同之处在于它使用SWAR方法，如公式（8）所示。

    当两个GPU内核的输入被限制为-1或+1（但不是其他情况）时，它们将返回相同的输出。 XNOR内核比基准内核快约23倍，比内核快3.4倍
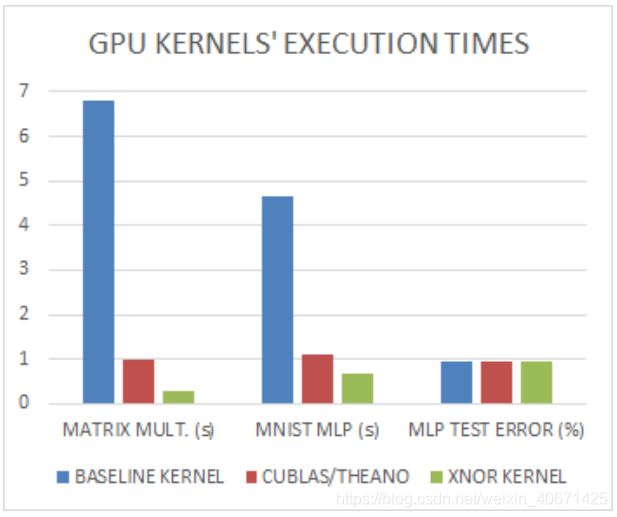
    如图3所示，其速度是cuBLAS的3倍。最后但并非最不重要的一点是，第2节中的MLP使用XNOR内核的速度是使用基线内核的速度的7倍，而不会损失任何分类精度（参见图3）。

   图3.前三列表示在GTX750 Nvidia GPU上执行8192×8192×8192（二进制）矩阵乘法所需的时间，具体取决于所使用的内核。 我们可以看到，我们的XNOR内核比基准内核快23倍，比cuBLAS快3.4倍。 接下来的三列表示在完整的MNIST测试集上从第2节运行MLP所花费的时间。 由于MNIST的图像不是二进制图像，因此第一层的计算始终由基线内核执行。 最后三列显示MLP准确性不取决于使用哪个内核。

5. 讨论和相关工作

    直到最近，人们仍认为使用极低精度的网络（在极端情况下为二进制）对网络性能具有很高的破坏性；？ 通过显示即使将所有神经元和权重二值化为±1也可以实现良好的性能，显示出相反的结果。 这是通过使用期望反向传播（EBP）（一种变型贝叶斯方法）完成的，该方法通过更新权重的后验分布来推断具有二元权重和神经元的网络。 这些分布通过反向传播（BP）算法通过区分其参数（例如平均值）来更新。 Esser等。 （2015年）使用非常类似于EBP的方法在运行时实施了一个完全二进制的网络，显示了能源效率的显着提高。 EBP的缺点是二值化参数仅在推断过程中使用。

    EBP背后的概率思想在Courbariaux等人的BinaryConnect算法中得到了扩展。 （2015）。在BinaryConnect中，权重的实值版本被保存，并用作二进制化过程的关键参考。二值化噪声在不同权重之间是独立的，无论是通过构造（通过使用随机量化）还是通过假设（通常是简化的方法；请参见Spang（1962）），该噪声对下一神经元的输入几乎没有影响，因为该输入是一个总和。因此，只需忽略更新中的二值化噪声，就可以通过反向传播误差来更新实值版本，使用这种方法，Courbariaux等人（2015年）率先对CNN中的权重进行了二值化并实现了如前所述（Wan等人，2013），他们还指出，噪声权重提供了一种形式化的正则化形式，可以帮助改善泛化性（Wan等人，2013年）。全精度神经元。

    Lin等。 （2015年）的工作延续了Courbariaux等人的工作。 （2015年）通过量化网络每一层的表示进行反向传播过程，通过限制两个整数的幂的神经元值将剩余的一些乘法转换为二进制移位。 Lin等。 （2015）的作品和我们的作品似乎具有相似的特征。 但是，他们的方法在测试阶段继续使用全精度权重。 此外，林等。 （2015）只量化神经元在反向传播过程中，而不是在正向传播。

    其他研究（Baldassi等人，2015）表明，在一台具有随机输入的机器中，完全二进制训练和测试是可能的，其中仅调整一个权重层。 Judd等。和龚等。旨在通过使用量化或矩阵分解方法来压缩经过充分训练的高精度网络。这些方法需要使用完全精确的权重和神经元来训练网络，因此需要所提出的BNN算法避免大量的MAC操作。 Hwang＆Sung（2014）专注于定点神经网络设计，并实现了几乎与浮点架构相同的性能。 Kim等。 （2014年）提供的证据表明，在专用电路上使用的具有三重权重的DNN消耗的功率非常低，并且只能在运行时使用片上存储器进行操作。 Sung等。还表明神经网络具有8位精度的令人满意的经验性能。 Kim＆Paris（2015）用二进制权重和激活重新训练了神经网络。

    到目前为止，据我们所知，在深层网络的推理阶段和整个训练阶段，还没有成功地将权重和神经元二值化。这是在当前工作中实现的。我们依赖于二值化可以随机完成，也可以近似为随机噪声的想法。以前是由Courbariaux等人为权重完成的。 （2015年），但我们的BNN将其扩展到激活。请注意，二进制激活对于ConvNets特别重要，因为ConvNets中的神经元通常多于自由权重。这样可以在运行时以及训练过程中的正向传播阶段对二值化DNN进行高效操作。而且，我们的训练方法几乎没有乘法，因此可以在专用硬件中有效地实现。但是，我们必须保存全精度权重的值。这是训练期间仍然存在的计算瓶颈，因为它需要相对较高的能源。将来可能会使用新颖的存储设备来缓解此问题。参见例如（Soudry et al。）。

结论

    在运行时以及在训练时计算参数梯度时，我们引入了具有二进制权重和激活的BNN，DNN（请参见第1节）。我们在两个不同的框架Torch7和Theano上进行了两组实验，结果表明可以在MNIST，CIFAR-10和SVHN上训练BNN，并获得近乎start-of-the-art的结果（请参阅第2节）。 此外，在前向遍历（在运行时和训练时）中，BNN大大减少了内存大小和访问量，并用按位运算代替了大多数算术运算，这可能导致功率效率的极大提高（请参阅第3节）。最后但并非最不重要的一点是，我们对二进制矩阵乘法GPU内核进行了编程，使用它可以使MNIST MLP的运行速度比未优化的GPU内核快7倍，而不会损失任何分类精度（请参见第4节）。未来的工作应探索如何将加速范围扩展到训练时间（例如，通过对某些梯度进行二值化），还将基准测试结果扩展到其他模型（例如RNN）和数据集（例如ImageNet）。