使用numpy编写神经网络,完成boston房价预测问题
from sklearn.datasets import load_boston
import numpy as np
import matplotlib.pyplot as plt
def load_data():
data1 = load_boston()
data = (data1)['data']
target =(data1)['target'][:, np.newaxis]
data = np.hstack((data,target))
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
training_data.sum(axis=0) / training_data.shape[0]
for i in range(data.shape[1]):
data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Network(object):
def __init__(self, num_of_weights):
np.random.seed(0)
self.n_hidden = 10
self.w1 = np.random.randn(num_of_weights,n_hidden)
self.b1 = np.zeros(n_hidden)
self.w2 = np.random.rand(n_hidden,1)
self.b2 = np.zeros(1)
def Relu(self,x):
return np.where(x < 0,0,x)
def MSE_loss(self, y,y_pred):
return np.mean(np.square(y_pred - y))
def Linear(self,x,w,b):
z = x.dot(w) + b
return z
def back_gradient(self, y_pred, y,s1):
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = s1.T.dot(grad_y_pred)
grad_temp_relu = grad_y_pred.dot(self.w2.T)
grad_temp_relu[l1 < 0] = 0
grad_w1 = x.T.dot(grad_temp_relu)
return grad_w1, grad_w2
def update(self, grad_w1,rad_w2,learning_rate):
self.w1 -= learning_rate * grad_w1
self.w2 -= learning_rate * grad_w2
def train(self, x, y, iterations, learning_rate):
losses = []
for t in range(num_iterations):
l1 = self.Linear(x,self.w1,self.b1)
s1 = self.Relu(l1)
y_pred = self.Linear(s1,self.w2,self.b2)
loss = MSE_loss(y,y_pred)
losses.append(loss)
grad_w1,grad_w2 = self.back_gradient(y_pred, y,s1)
self.update(grad_w1,grad_w2,learning_rate)
return losses
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
net = Network(13)
num_iterations=50000
losses = net.train(x,y, iterations = num_iterations, learning_rate = 1e-6)
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.rcParams['font.sans-serif'] = ['SimHei']
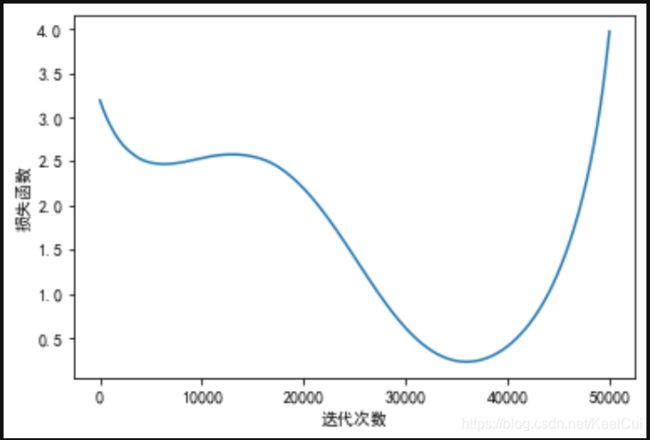
plt.plot(plot_x, plot_y)
plt.xlabel('迭代次数')
plt.ylabel('损失函数')
plt.show()
print('w1 = {}\n w2 = {}'.format(w1,w2))
w1 = [[-1.12066809 -0.05560125 1.56254881 -0.79259637 -0.56585845 -0.31344767
0.25956291 0.49606333 1.26064615 0.49922422]
[-0.09460359 1.26101552 0.7274505 -1.4818753 2.51345551 1.75322815
-0.14208139 0.32143129 1.30204663 -0.17314904]
[ 0.71019447 1.01302204 -1.07031898 -0.60041226 0.92283182 0.45112563
0.87624858 -0.14059358 -0.29614417 -2.00303366]
[-1.11149904 -0.00808231 0.76497792 0.49634308 -0.12666605 -0.27289471
0.18916355 -0.02118366 1.25239094 0.15216091]
[-1.49136207 -1.36451559 1.45900166 -1.16289422 0.76574408 -0.28322769
-0.21107519 -0.15747864 1.18936901 -0.19661487]
[-0.02461259 -1.51277616 0.22567877 0.52844018 0.23670959 1.39525051
0.06751154 0.26256106 1.62063659 -1.5527056 ]
[-0.46590831 1.32962428 0.86458885 0.66238096 0.83646239 0.31778254
1.57503711 0.32932899 0.20085178 0.16062881]
[ 0.19316434 -1.09989625 0.80357259 -0.12783974 1.8167787 -0.07130515
0.45034406 0.26309426 -0.60644811 0.99359157]
[ 1.81524734 -0.11956975 -0.37423825 -0.34307674 -1.8869721 -0.19775474
0.2056634 0.93600864 0.94421473 -0.41722462]
[-0.34584039 1.01422331 -0.24162305 -0.49232518 1.39184543 1.01617002
-0.02836443 -0.66217765 -1.99960662 0.58510313]
[-0.89450238 -1.93684923 1.54877234 0.64142481 -1.13322238 -1.20011165
0.8543447 -0.82590095 1.31338642 0.61766115]
[ 0.53036753 0.41382651 0.1981755 0.87670966 -0.45362095 0.08777864
0.75457729 0.54330661 -1.17656106 -0.5007381 ]
[ 0.22360996 -0.4697619 1.71964262 -0.39394983 -0.15954374 0.76122302
0.29876607 -0.15120541 -0.74536015 0.30451732]]
w2 = [[ 0.28553235]
[ 0.16834442]
[-0.02368562]
[ 0.07504223]
[-0.18749866]
[-0.04594007]
[-0.18557294]
[ 0.63719667]
[ 0.28921447]
[-0.18523397]]
