tslearn使用轮廓系数（silhouette_score）评估KShape聚类效果

前言

tslearn和sklearn一样，是一款优秀的机器学习框架，tslearn更偏向于处理时间序列问题，如其聚类模块就包含了DTW（Dynamic Time Warping）等算法及变种，也提供了轮廓系数对聚类效果评估，十分方便。但可惜，tslearn似乎没有提供对KShape聚类的评估方法，而且tslearn用的人也不多，官方文档也是很 “简洁”，网上也搜不到多少相关文章，所以这里也就记录下自己的踩坑过程

轮廓系数评估接口调用

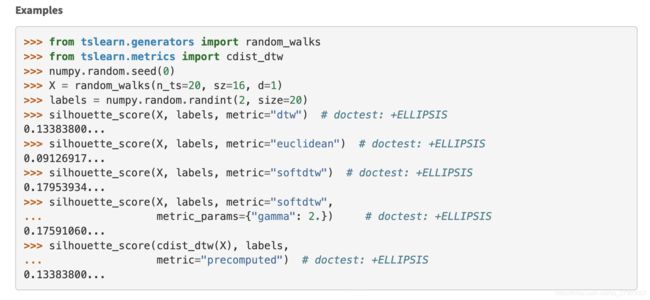
先看官方例子，这里X是一个三维的numpy数组，代表20段时间序列，每段序列16个时间点。labels代表每段时间序列（每条时间曲线）的聚类结果，metric是每条时间曲线之间相似度度量方法，可以看到官方提供了dtw-dba、softdtw以及欧氏距离三种相似度度量方法，但没有关于KShape聚类的。

注意到最后一行，metric=“precomputed”，说明官方提供了用户自定义的距离度量方法，很好，那么使用silhouette_score评估KShape的关键就在此了。又注意到precomputed的时候，参数传的是cdist_dtw(X)，而其他传的是X，有什么区别？

打印

醒目的零对角线告诉我们这是X与X自身的距离矩阵，相同时间曲线的距离为零。这样其实也就对了，轮廓系数的计算本来就需要比较当前元素到同簇下其他元素的距离，以及与其他簇下的距离，因此需要得到每个元素之间的距离，X与X自身的距离矩阵恰好解决了这点，而计算其他簇就需要labels标签指明哪些元素属于哪些类

问题来了，那我怎么知道KShape聚类用什么方法度量相似度？不清楚其用的方法，就得不到距离矩阵，也就无法使用precomputed。自己看论文仿写一个？仿写的若与源码的实现不同，细节上的差距也可能会导致轮廓系数的评估不准

源码找突破口

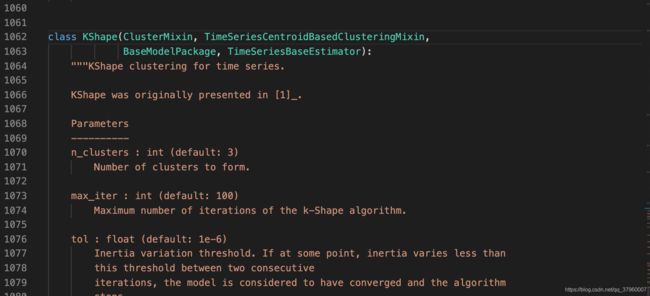
我们现在想要的是KShape对时间序列相似度、也就是距离的计算方法，而且要原封不动，不能仿写，所以只能去KShape源码里寻找结果。点进KShape，大概是一千多行的位置

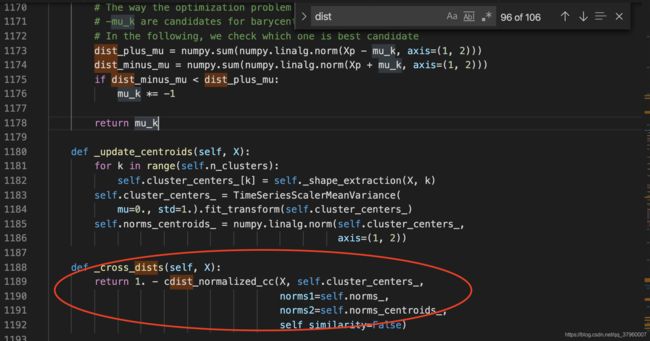
既然是距离，就在KShape行数往后搜索dist，看看能否找到相关线索

 

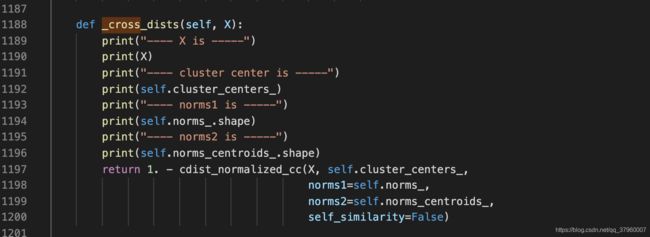
一个醒目的函数名引起了我的注意，cross_dist，交叉距离，似乎有点距离矩阵的味道。于是我查阅了KShape官方文档，看到有这么一条引用：

说明tslearn里的KShape源码是按该论文实现的。在论文k-Shape: Efficient and Accurate Clustering of Time Series中，看到了这样一个公式：

表达式 1 - max(xxx)，这不正好和_cross_dist函数的结构一样？就差一个max。

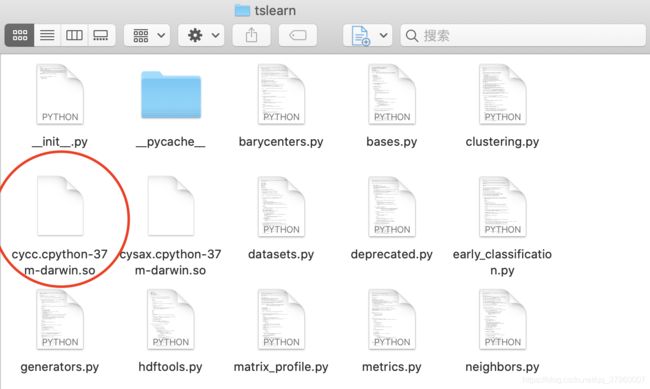
继续点进 cdist_normalized_cc 函数，发现点不进去，又去import的地方继续点，发现 tslearn.cycc 也点不进去

最后发现cycc是 .so文件

既然是调用的其他拓展语言的库，就只能去github上看了。找到官方的github后点开cycc.pyx文件

在 cdist_normalized_cc 函数的最后有一个max！这不正好完全与论文中的公式对应了？也就是说KShape聚类采用的是一个叫SBD的方法进行距离计算的，其实现就在github的 cycc.pyx文件中，也就是说我们只需拿到这段代码就可以生成X的距离矩阵，从而可以使用precomputed进行轮廓系数对KShape的聚类效果评估

参数确定

可以看到 cdist_normalized_cc 有五个参数，dataset1和dataset2代表计算两者之间的距离矩阵，那么这两个参数都填 X 即可。还有两个norms1和norms2参数，看论文里的公式，向量平方后开根号，似乎在求向量的模长。实验一下，直接修改源码，打印norms的值

按照官方的案例，random_walk生成X和labels、初始化KShape并调用 fit 函数后，结果如下：

这验证了norms确实是向量的模长，于是norms参数也解决了。至于self_similarity不动它，设置成False即可

测试

这里有个坑，如果直接在你自己的py文件中 import tslearn.cycc会报错，可能是so文件比较特殊。这里采用了另一种方式进行测试，即再次直接修改源码，如下：

增加_get_norms函数和_my_cross_dist函数，前者负责计算模长，后者返回时序集合X的距离矩阵，即X中每个元素ti之间的距离所形成的矩阵。参数则按照前一小节的方式传

下面先进行距离矩阵的测试

import numpy as np
from tslearn.clustering import KShape
from tslearn.generators import random_walks

def test_cross_dist():
    seed = 0
    num_cluster = 2
    ks = KShape(n_clusters= num_cluster ,n_init= 5 ,verbose= True ,random_state=seed)
    X = random_walks(n_ts=4, sz=2, d=1) * 10
    dists = ks._my_cross_dist(X)
    print(dists)

test_cross_dist()

随机生成四条曲线，每条两个时间点，调用_my_cross_dist测试，结果如下

[[ 6.68621811e-08  5.90374654e-01  3.93694605e-01  2.73371849e-01]
 [ 5.90374654e-01  1.06040988e-08  1.06048454e+00  1.23859603e+00]
 [ 3.93694605e-01  1.06048454e+00 -9.46784942e-08  9.19879423e-02]
 [ 2.73371849e-01  1.23859603e+00  9.19879423e-02 -1.73142627e-08]]

可以看到对角线已经到了负8次方，几乎是零了。距离矩阵测试成功

下面使用轮廓系数测试KShape聚类

import numpy as np
from tslearn.generators import random_walks
import tslearn.metrics as metrics
from tslearn.clustering import silhouette_score

def test_kshape_silhouette_score():
    seed = 0
    num_cluster = 2
    ks = KShape(n_clusters= num_cluster ,n_init= 5 ,verbose= True ,random_state=seed)
    X = random_walks(n_ts=20, sz=16, d=1) * 10
    #随机生成标签（即乱猜聚类结果）
    y_pred = np.random.randint(2, size=20)
    dists = ks._my_cross_dist(X)
    #这步重要，由于计算出的距离矩阵只是负8次方，还不是真正的零，得替换，否则会报错
    np.fill_diagonal(dists,0)
    #计算轮廓系数
    score = silhouette_score(dists,y_pred,metric="precomputed")
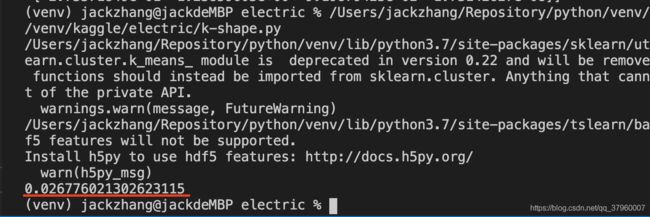
    print(score)

在随机设置标签的情况下，理论上轮廓系数应该是零，表示一个元素既可以属于这个簇，也可以属于另一个簇，运行

可以看到，轮廓系数十分接近零，测试成功

实战

随机情况下测试成功还不够，下面使用KShape聚类测试真实生产数据，并使用轮廓系数进行评估

import numpy as np
import glob
from tslearn.clustering import KShape
from tslearn.preprocessing import TimeSeriesScalerMeanVariance
import matplotlib.pyplot as plt
from tslearn.generators import random_walks
import tslearn.metrics as metrics
#自定义数据处理
import data_process

# X，100个数据，每个2800+维
X = np.loadtxt("top100.txt",dtype=np.float,delimiter=",")
# 降维，2800维将成30维
X = data_process.downsample(X,30)
seed = 0

# elbow = 4（elbow法则寻找最佳聚类个数）
def test_elbow():
    global X,seed
    distortions = []
    X = TimeSeriesScalerMeanVariance(mu= 0.0 ,std= 1.0 ).fit_transform(X)
    #1 to 10 clusters 
    for i in  range ( 2 , 7 ):
        ks = KShape(n_clusters=i, n_init= 5 ,verbose= True ,random_state=seed)
        # Perform clustering calculation
        ks.fit(X)
        #ks.fit will give you ks.inertia_ You can 
        #inertia_
        distortions.append(ks.inertia_)
    plt.plot(range ( 2 , 7 ), distortions, marker= 'o' )
    plt.xlabel( 'Number of clusters' )
    plt.ylabel( 'Distortion' )
    plt.show()


def test_k_shape():
    global X,seed
    np.random.seed(seed)
    num_cluster = 4
    # 标准化数据
    X = TimeSeriesScalerMeanVariance(mu= 0.0 ,std= 1.0 ).fit_transform(X)
    ks = KShape(n_clusters= num_cluster ,n_init= 5 ,verbose= True ,random_state=seed)
    y_pred = ks.fit_predict(X)
    dists = ks._my_cross_dist(X)
    np.fill_diagonal(dists,0)
    score = silhouette_score(dists,y_pred,metric="precomputed")
    print(X.shape)
    print(y_pred.shape)
    print("silhouette_score: " + str(score))
    for yi in range(num_cluster):
        plt.subplot(2, 2, yi + 1)
        for xx in X[y_pred == yi]:
            plt.plot(xx.ravel(), "k-", alpha=.3)
        plt.plot(ks.cluster_centers_[yi].ravel(), "r-")
        plt.text(0.55, 0.85,'Cluster %d' % (yi + 1),
                transform=plt.gca().transAxes)
        if yi == 1:
            plt.title("SBD" + "  $k$-shape")

    plt.tight_layout()
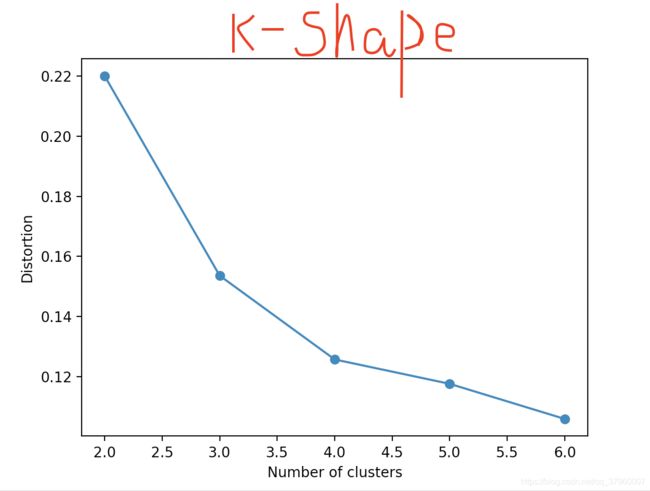
    plt.show()

elbow法则，4这里有最大弯曲度，确定是4聚类

未降维之前的时序数据聚类效果：

打印结果：

(100, 2858, 1)
(100,)
silhouette_score: 0.5171964754458871

降维之后的聚类效果：

打印结果：

(100, 30, 1)
(100,)
silhouette_score: 0.5510349154221014

KShape聚类评价

不同算法的聚类效果图对比才是最好、最简洁的评价，上图

K-Means + 欧氏距离（同一数据集）# silhouette_score: 0.5095828273645443

K-Means + DTW + DBA  # silhouette_score: 0.5878368758366767

K-Means + SoftDTW  # silhouette_score: 0.7473192701567871