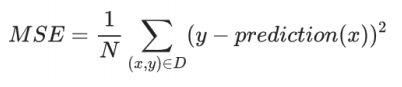学习笔记 | 深度学习开发—TensorFlow实践(线性回归 tensorflow实战)

监督式机器学习

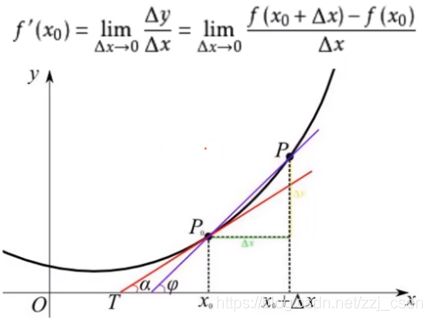
1.简单的线性回归案例

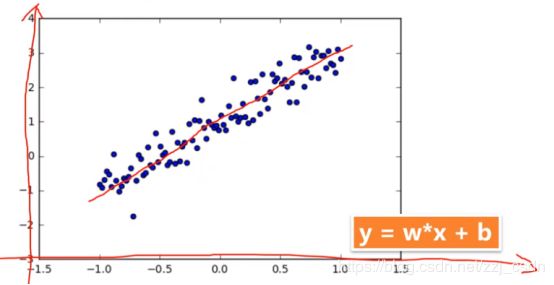
确定y=w*x+b这样的方程，其中w和b的值

2.术语：标签和特征

标签：是我们要预测的真实事物：y,线性回归中的y变量

特征：是指用于描述数据的输入变量：xi线性回归中的{x1,x2,x3,……,xn}变量

3.样本和模型

样本是指数据的特定实例：x

有标签样本具有{特征，标签}：{x，y}：用于训练模型

无标签样本具有{特征，？}：{x,?}:用于对新数据做出预测

模型可将样本映射到预测标签：y'

由模型的内部参数定义，这些内部参数值是通过学习得到的

4.训练

训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值。

在监督学习中，机器学习算法通过以下方式构建模型：

检查多个样本并尝试找出最大限度地减少损失的模型，这一过程称为经验风险最小化。

5.损失

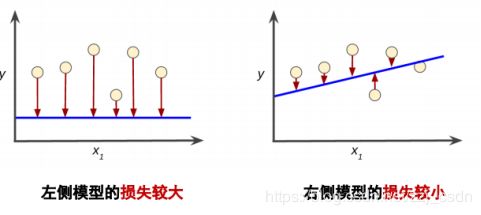
损失是对糟糕预测的惩罚：损失是一个数值，表示对于单个样本而言模型预测的准确程度

如果模型的预测完全准确，则损失为零，否则损失会较大训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差

6.定义损失函数

L1损失：基于模型预测的值与标签的实际值之差的绝对值

平方损失：一种常见的损失函数，又称为 L2 损失

均方误差 (MSE) 指的是每个样本的平均平方损失

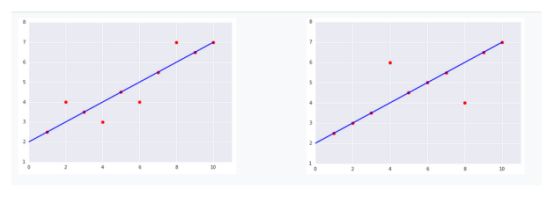
以下曲线图中显示的两个数据集，哪个数据集的均方误差 (MSE) 较高？

答案：第二个比较高，损失大

模型训练与降低损失

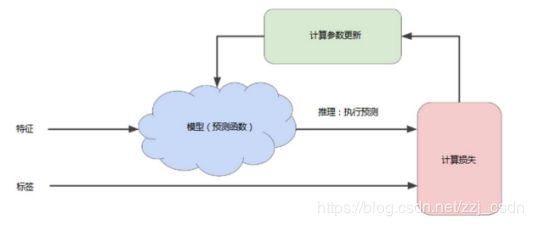
1.训练模型的迭代方法

2.模型训练要点

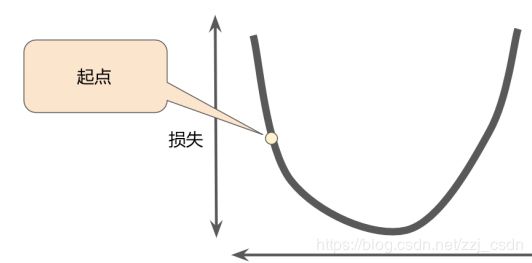
首先对权重w和偏差b进行初始猜测

然后反复调整这些猜测

直到获得损失可能最低的权重和偏差为止

3.收敛

在学习优化过程中，机器学习系统将根据所有标签去重新评估所有特征，为损失函数生成一个新值，而该值又产生新的参数值。

通常，您可以不断迭代，直到总体损失不再变化或至少变化极其缓慢为止。这时候，我们可以说该模型已收敛

4.计算损失例子

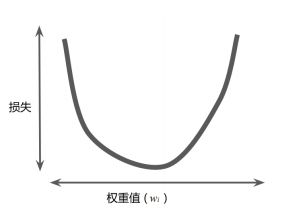
该线性回归问题产生的损失与权重图为凸形

凸形问题只有一个最低点；即只存在一个斜率正好为 0 的位置，这个最小值就是损失函数收敛之处

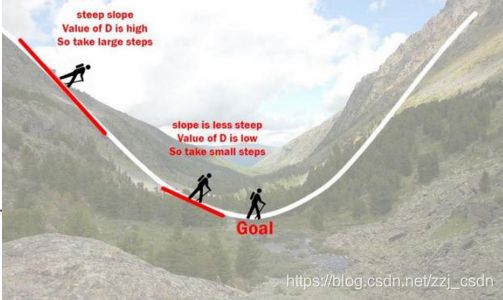
梯度下降法

梯度：一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大

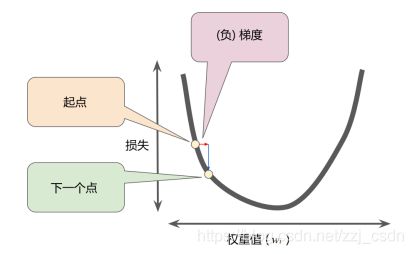
梯度是矢量:具有方向和大小

沿着负梯度方向进行下一步探索

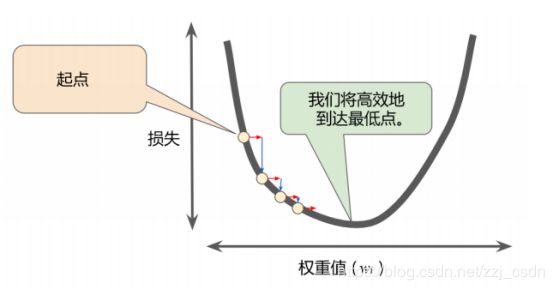
学习率

沿着负梯度方向进行下一步探索，前进多少合适呢？

用梯度乘以一个称为学习速率（有时也称为步长）的标量，

以确定下一个点的位置

例如：如果梯度大小为2.5，学习速率为0.01，则梯度下降法算法会选择距离前一个点0.025的位置作为下一个点

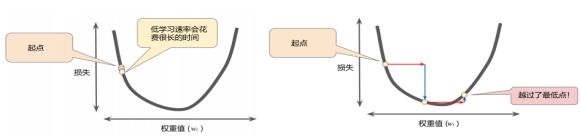
                        梯度学习速率过小             梯度学习速率过大

超参数

在机器学习中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，选择一组好的超参数，可以提高学习的性能和效果超参数是编程人员在机器学习算法中用于调整的旋钮 典型超参数：学习率、神经网络的隐含层数量……