PRML读书笔记 第十章 近似推断（1）

  从今天起开始更新关于PRML书籍当中的一些学习笔记和感悟心得。目前先从最近所学的部分开始更新，会在未来一段时间当中补更之前的章节所学内容。
 这篇文章主要简述一下变分估计方法的作用和基本概念，并详细对比变分近似法下解决线性回归问题和之前的统计方法解决线性问题的异同。

近似推断方法概述

• 近似推断方法的作用
   之前我们学习过利用极大似然估计等统计学方法对于各种模型（线性回归模型，混合高斯模型等等）进行处理。利用近似推断的方法其实与之前所使用的方法能够得到类似的结果，然而利用传统方法可能会出现比较难以处理的概率分布，或者参数过多计算复杂度过大的情况。这种时候我们就需要引入近似算法来计算相应的结果。

• 变分法
   我理解的变分法的主要思想是把我们所需求的后验概率 $p\left(Z|X\right)$ 近似为我们变分选择的一个量 $q\left(Z\right)$ ,再通过对于$q\left(Z\right)$ 进行一种类似于递归迭代的方法来进行求解。
   其在对边缘概率$\ln p\left(X\right)$进行分解$\ln p\left(X\right)=\zeta (q)+KL\left(q||p\right)$ 的时候使用了KL散度:
  $$KL\left(q||p\right)=-\int q\left(Z\right)\ln \{\frac{p\left(X,Z\right)}{q\left(Z\right)}\}dZ$$
   这其中KL散度曾经在VAE模型当中使用过，在VAE模型当中它所起到的作用也是作为我们所需概率分布的重要近似。
   分解概率分布的方法是一种比较常用的利用变分法进行计算的方法，也是后续所对比的几种方法中比较常用的。其步骤与EM算法类似，核心是限制
  $q\left(\mathbf{Z}\right)$的分布，将Z元素分解成若干个互不相交的组，即$q\left(\mathbf{Z}\right)={\prod }_{i=1}^M{q}_i\left(\mathbf{Z}\right)$
   那么对于$\zeta (q)$有下述变换：
  $$\begin{gathered} \zeta (q)=\int \prod _{i=1}{q}_i\{\ln p(\mathbf{X},\mathbf{Z})-\sum _{k=1}\ln q_i\}d\mathbf{Z} \\ =\int q_j\{\int \ln p(\mathbf{X},\mathbf{Z})\prod _{i\ne j}{q}_{i}d{\mathbf{Z}}_{\mathbf{j}}\}-\int q_j\ln q_{j}d{\mathbf{Z}}_{\mathbf{j}}+常数 \\ =\int q_j\ln \tilde{p}(\mathbf{X},\mathbf{Z})d{\mathbf{Z}}_{\mathbf{j}}-\int q_j\ln q_{j}d{\mathbf{Z}}_{\mathbf{j}}+常数 \end{gathered}$$

 这其中我们定义了$\ln \tilde{p}(\mathbf{X},\mathbf{Z})=E_{i\ne j}[\ln p(\mathbf{X},\mathbf{Z})]+常数$
 而$E_{i\ne j}[\ln p(\mathbf{X},\mathbf{Z})]=\int \ln p(\mathbf{X},\mathbf{Z}){\prod }_{i\ne j}{q}_{i}d{\mathbf{Z}}_{\mathbf{j}}$
 其中$\ln q_j^{\ast }(Z_j)=E_{i\ne j}[\ln p(\mathbf{X},\mathbf{Z})]+常数$（此式是日后解决问题的重要公式）
 利用上述方法我们可以计算出每一个$q({\mathbf{Z}}_{\mathbf{j}})$，从而得到近似$p\left(Z|X\right)$ 的结果。
 可能上述的方法有一些复杂，理论性比较强，今天我们主要通过讲述一个例子，即一元高斯分布的操作方法，来温习一下之前我们用极大似然估计法的做法，同时也对比一下利用变分估计方法的新的做法。

一元高斯问题的传统做法和变分推断方法

• 所求问题
   我们所面对的问题是给定$\mathbf{x}$的观测值$D=\{x_1,x_2...x_n\}$，并且知道其分布满足正态分布的情况下其后验概率所满足的概率分布。（注意：这里所求的是后验概率所满足的概率分布，与数理统计当中简单地利用矩估计或者极大似然估计方法不同，那样只能做点估计或者对置信区间进行估计，而这里要对其概率分布进行估计。）

• 统计方法
   回顾一下之前利用贝叶斯统计方法，可以利用共轭先验分布来对其进行求解。共轭先验分布的原理是找到有关于参数$\theta$的一个先验分布$\pi (\theta )$，若有$\pi (\theta |x)\propto p(x|\theta )\pi (\theta )$，则称$\pi (\theta )$为一个共轭先验分布。利用共轭先验分布的性质我们可以用类似于配方法的办法求得其后验概率分布。
   对于方差已知的正态分布，其均值的后验概率分布依然服从正态分布。
   假设$\pi (\theta )$服从一个$N(\mu ,{\tau }^2)$的正态分布。那么其样本和均值的联合概率分布为：$$h(x,\theta )=k_{1}exp\{-\frac{1}{2}[\frac{n{\theta }^2-2n\theta \bar{x}+{\sum }_{i=1}^n{x}_i^2}{{\sigma }^2}+\frac{{\theta }^2-2\mu \theta +{\mu }^2}{{\tau }^2}]\}$$
  我们令${\sigma }_0^2=\frac{{\sigma }^2}{\pi }$,$A=\frac{1}{{\sigma }_0^2}+\frac{1}{{\tau }^2}$,$B=\frac{x}{{\sigma }_0^2}+\frac{\mu }{{\tau }^2}$,$C=\frac{1}{{\sigma }^2}{\sum }_{i=1}^n{x}_i^2+\frac{{\mu }^2}{{\tau }^2}$
  由联合概率函数积分可得边缘概率分布：$$m(x)={\int }_{-\infty }^{+\infty }h(x,\theta )d\theta =k_2(\frac{2\pi }{A}{)}^{\frac{1}{2}}$$
  将上述两式相除即可得到后验概率分布：
  $$\pi (\theta |x)=(\frac{2\pi }{A}{)}^{-\frac{1}{2}}exp\{-\frac{(\theta -B/A)}{2/A}\}$$
  即可得到相关的后验概率分布。

 对于已知均值求解方差的情况与此计算过程相同，但更加繁琐了一些 ，其满足一个倒伽马分布。即其先验概率分布$\pi ({\sigma }^2)=\frac{{\lambda }^{\alpha }}{\Gamma (\alpha )}(\frac{1}{{\sigma }^2}{)}^{\alpha +1}{e}^{-\lambda /{\sigma }^2}$
后验概率$\pi ({\sigma }^2|x)\propto p(x|{\sigma }^2)\pi ({\sigma }^2)$
从上述可以看出，通过统计学方法，得以很轻易的解决这个问题。

• 变分方法
   首先按照之前的推导方法，要选择一种概率分布的分解方式，这里最简单的分解方式就是$q(\mu ,\tau )=q_{\mu }(\mu )q_{\tau }(\tau )$
  按照所推导结果$$\begin{gathered} \ln q_{\mu }^{\ast }(\mu )=E_{\tau }[\ln p(D|\mu ,\tau )+\ln p(\mu |\tau )]+常数 \\ =-\frac{E[\tau ]}{2}\{{\lambda }_0(\mu -{\mu }_0{)}^2+\sum _{n=1}^N(x_n-\mu {)}^2\}+常数 \end{gathered}$$
   由此我们可以看出$q_{\mu }(\mu )$也是一个服从均值为$\frac{{\lambda }_0{\mu }_0+N\bar{x}}{{\lambda }_0+N}$，方差为$({\lambda }_0+N)E[\tau ]$
   同样对于$q_{\tau }^{\ast }(\tau )$的估计，利用
  $$\begin{gathered} \ln q_{\tau }^{\ast }(\tau )=E_{\mu }[\ln p(D|\mu ,\tau )+\ln p(\mu |\tau )]+\ln p(\tau )+常数 \\ =(a_0-1)\ln \tau -b_0\tau +\frac{N+1}{2}\ln \tau -\frac{\tau }{2}{E}_{\mu }[\sum _{n=1}^N(x_n-\mu {)}^2+{\lambda }_0(\mu -{\mu }_0{)}^2] \end{gathered}$$
   看出其与统计学推出结果服从相同的分布（我们在上文中统计学方法使用的${\sigma }^2$是方差，而此处用的$\tau$是精度，其具有倒数的对应关系。故形式相同）
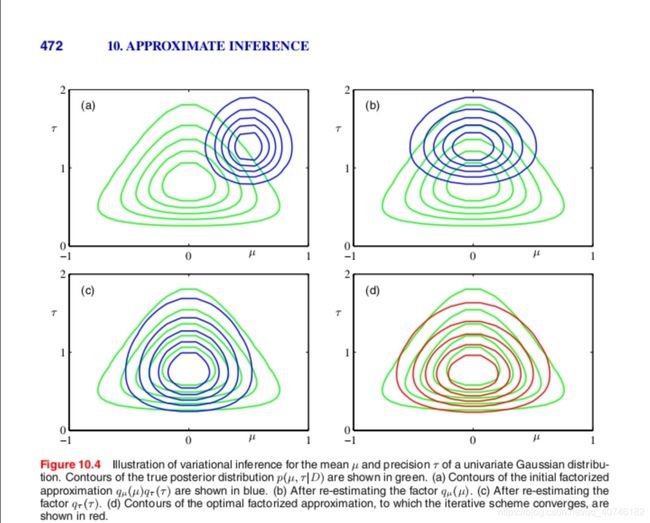
   变分方法的后续过程需要对于初始迭代的$E[\mu ]$或者$E[\tau ]$先进行一次估计，再利用此初值进行迭代，从PRML的教材的图中可以看到其具有较好的效果。
  

心得体会

 通过简单的例子，对比之前的EM方法等初识了变分法的作用。感觉在计算机数值解数值分析类问题当中，使用迭代的方法似乎一直是要优于直接求解的方法的。
 下一篇将会更新EM方法和贝叶斯回归方法与变分法的对比，实际上大部分之前所学的算法都可以利用变分法来找到他的近似解。
顺便也复习了一下之前共轭先验分布当中的部分知识，进一步理解了KL散度在各种应用当中的作用。在撰写这个博客的时候也熟悉了Latex公式编辑~
 如果有理解有误希望能够及时指出，也希望能够有同时学这本书的大佬一起讨论指点。