sklearn的波士顿房价数据是经典的回归数据集。在MOOC的课程《用Python玩转数据》最终的实践课程中就用它来进行简单的数据分析,以及模型拟合。
文章将主要分为2部分:
1、使用sklearn的linear_model进行多元线性回归拟合;同时使用非线性回归模型来拟合(暂时还没想好用哪个?xgboost,还是SVM?)。
2、使用tensorflow建立回归模型拟合。
一、使用sklearn linear_regression 模型拟合boston房价datasets
from sklearn import datasets
from sklearn import linear_model
from sklearn.cross_validation import train_test_split
from sklearn import metrics
import os
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
'''----------load 数据集-----------'''
dataset = datasets.load_boston()
# x 训练特征:['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
x = dataset.data
target = dataset.target
#把label变为(?, 1)维度,为了使用下面的数据集合分割
y = np.reshape(target,(len(target), 1))
#讲数据集1:3比例分割为 测试集:训练集
x_train, x_verify, y_train, y_verify = train_test_split(x, y, random_state=1)
'''
x_train的shape:(379, 13)
y_train的shape:(379, 1)
x_verify的shape:(127, 13)
y_verify 的shape:(127, 1)
'''
'''----------定义线性回归模型,进行训练、预测-----------'''
lr = linear_model.LinearRegression()
lr.fit(x_train,y_train)
y_pred = lr.predict(x_verify)
'''----------图形化预测结果-----------'''
#只显示前50个预测结果,太多的话看起来不直观
plt.xlim([0,50])
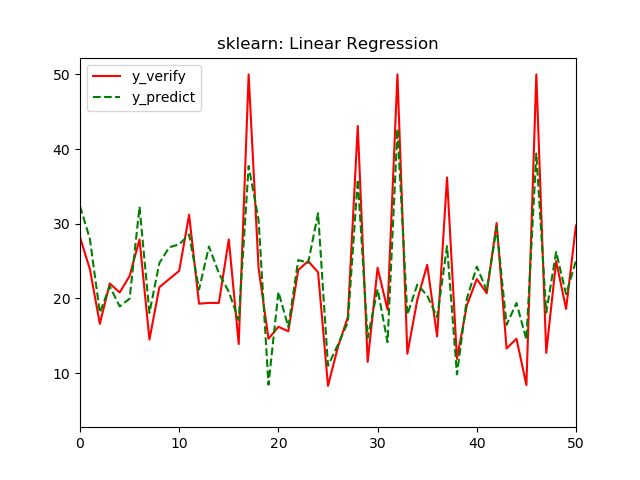
plt.plot( range(len(y_verify)), y_verify, 'r', label='y_verify')
plt.plot( range(len(y_pred)), y_pred, 'g--', label='y_predict' )
plt.title('sklearn: Linear Regression')
plt.legend()
plt.savefig('lr/lr-13.png')
plt.show()
'''----------输出模型参数、评价模型-----------'''
print(lr.coef_)
print(lr.intercept_)
print("MSE:",metrics.mean_squared_error(y_verify,y_pred))
print("RMSE:",np.sqrt(metrics.mean_squared_error(y_verify,y_pred)))
#输出模型对应R-Square
print(lr.score(x_train,y_train))
print(lr.score(x_verify,y_verify))
结果如下:
[[-1.13256952e-01 5.70869807e-02 3.87621062e-02 2.43279795e+00
-2.12706290e+01 2.86930027e+00 7.02105327e-03 -1.47118312e+00
3.05187368e-01 -1.06649888e-02 -9.97404179e-01 6.39833822e-03
-5.58425480e-01]]
-----------权重参数W
[45.23641585]
----------偏置bias
MSE: 21.88936943247483
RMSE: 4.678607638226872
----------MSE和RMSE都是表示衡量观测值同真值之间的偏差
0.7167286808673383
----------训练集的R-Square
0.7790257749137334
-----------测试集的R-Square
从图看,部分数据结果偏差不大,部分预测结果还有一定差距,从r-square来看拟合效果凑合。
R2 也叫确定系数(coefficient of determination),表示模 型对现实数据拟合的程度,它是皮尔逊相关系数的平方,从数值上说,R2介于 0~1 之间,越 接近 1 表示拟合效果越好,0.7以上 这个数字说明测试集中有 7 成多的数据可通过模型解释, 拟合效果较好,但还有一定的空间,一般认为超过 0.8 的模型拟合优度比较高,可以尝试使用非线性模型进行预测。
初学者可以先关注调整 R2 和 T 检验的 p 值,后续可以继续理解利 用 F 检验检查方程的整体显著性以及进行残差分析等,有兴趣的学习者可进行深入研究。
----(摘自MOOC《用Python玩转数据》)
特征选择:
sklearn中特征选择有很多种方法:
去除方差较小的特征:VarianceThreshold
单变量特征选择:SelectKBest、SelectPercentile、GenericUnivariateSelect
我们这里使用sklearn中SelectKBest函数进行特征选择,参数中的score_func选择:
分类:chi2----卡方检验
f_classif----方差分析,计算方差分析(ANOVA)的F值 (组间均方 / 组内均方)
mutual_info_classif----互信息,互信息方法可以捕捉任何一种统计依赖,但是作为非参数方法,需要更多的样本进行准确的估计
回归:f_regression----相关系数,计算每个变量与目标变量的相关系数,然后计算出F值和P值
mutual_info_regression----互信息,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度
https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SelectKBest.html
https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.f_regression.html
关于f_regression更具体解释,具体也可看文章:https://blog.csdn.net/jetFlow/article/details/78884619
我们的是回归问题,在这使用f_regression作为score_func进行筛选条件,在样本特征选选出 k 个的得分高的特征,默认 k = 10。波士顿房价问题中特征是13个,我们使用循环,看k值取多少合适。
MSE_list=[]
score_train=[]
score_verify=[]
for i in range(2,14):
x_new = SelectKBest(f_regression, k=i).fit_transform(x, target)
x_train, x_verify, y_train, y_verify = train_test_split(x_new, y, random_state=1)
y_train = y_train.reshape(-1)
train_data = np.insert(x_train, 0, values=y_train, axis=1)
y_t = train_data[:, 0].reshape(-1,1)
lr = linear_model.LinearRegression()
lr.fit(x_train,y_train)
y_pred = lr.predict(x_verify)
score_train.append(lr.score(x_train, y_train))
score_verify.append(lr.score(x_verify, y_verify))
MSE_list.append(metrics.mean_squared_error(y_verify,y_pred))
print('MSE_list:',MSE_list)
print('train_score:',score_train)
print('verify_score:',score_verify)
plt.subplot(2,1,1)
plt.plot(range(2,14),MSE_list)
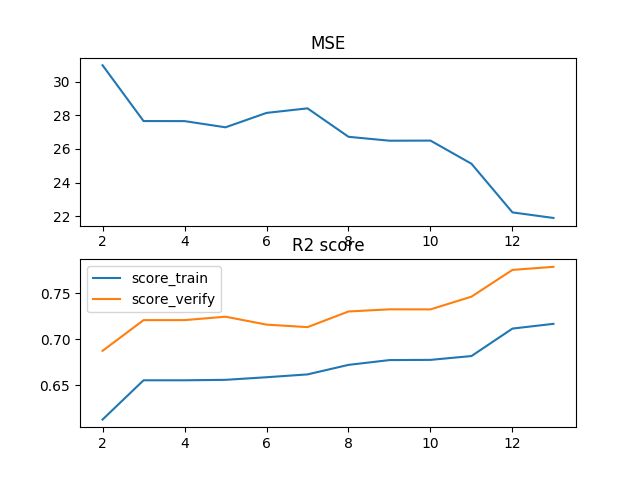
plt.title('MSE')
plt.subplot(2,1,2)
plt.plot(range(2,14),score_train,label='score_train')
plt.plot(range(2,14),score_verify,label='score_verify')
plt.legend()
plt.title('R2 score')
plt.savefig('feature_selection.png')
plt.show()
结果输出如下:
MSE_list: [30.97014521755215, 27.65412935105601, 27.651260247704577, 27.28301263897541, 28.13859216347999, 28.409333535357277, 26.719218376293934, 26.486798709462853, 26.493273792132474, 25.117759564415888, 22.228430426663383, 21.897765396049444]
train_score: [0.6124282780222445, 0.6552443540161836, 0.6552474484272307, 0.6557456371776518, 0.6585732416001857, 0.6616656815463774, 0.6720552272075447, 0.6772752178717331, 0.6775049108616567, 0.6816762497813345, 0.7116255502702171, 0.7168057552393374]
verify_score: [0.6873549116447073, 0.7208302494671684, 0.7208592132019043, 0.7245766903192703, 0.7159395743433946, 0.7132064273226943, 0.7302682202049733, 0.7326145077913399, 0.7325491415239512, 0.7464350230475125, 0.775602938057746, 0.7789410172622863]
可见还是 k=13 时,训练集和测试集上R2得分都是最高的。(这里的R2得分与上面完整模型的分数略有偏差,我认为是因为sklearn的版本的差异导致,不过分数差别不大,不影响我们对模型的评估)
所以,综上就是使用sklearn的线性回归模型对波士顿房价预测的拟合情况。