划分数组使得子数组和相等

2018-08-13 17:35:09

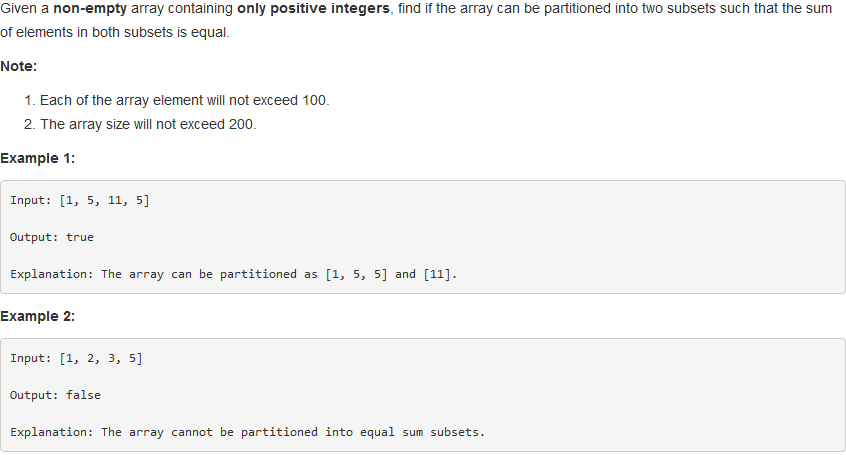
一、Partition Equal Subset Sum

问题描述：

问题求解：

二分和本质上其实是一个背包问题，就是问是否存在一种情况，使得可以填满一个sum/2的背包。

    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int i : nums) sum += i;
        if (sum % 2 != 0) return false;
        sum /= 2;
        boolean dp[] = new boolean[sum + 1];
        dp[0] = true;
        for (int num : nums) {
            for (int i = sum; i >= num; i--) {
                dp[i] = dp[i] || dp[i - num];
            }
        }
        return dp[sum];
    }

 

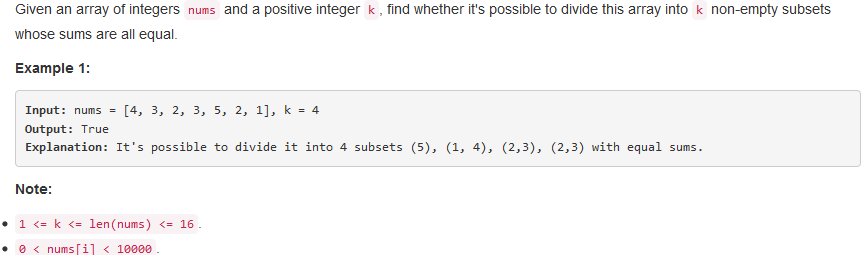
二、Partition to K Equal Sum Subsets

问题描述：

问题求解：

Brute Force，本质是使用组合数进行解空间的遍历。

PS.使用排列数也可以，但是效率比组合数要慢上不少。

    public boolean canPartitionKSubsets(int[] nums, int k) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) sum += nums[i];
        if (sum % k != 0) return false;
        Arrays.sort(nums);
        int eachSum = sum / k;
        int[] visited = new int[nums.length];
        return helper(nums, eachSum, 0, visited, 0, k);
    }

    private boolean helper(int[] nums, int eachSum, int curSum, int[] visited, int start, int k) {
        if (k == 0) return true;
        if (curSum > eachSum) return false;
        if (curSum == eachSum) return helper(nums, eachSum, 0, visited, 0, k - 1);
        for (int i = start; i < nums.length; i++) {
            if (visited[i] == 1 || (i > start && nums[i] == nums[i - 1] && visited[i - 1] == 0)) continue;
            visited[i] = 1;
            if (helper(nums, eachSum, curSum + nums[i], visited, i + 1, k)) return true;
            visited[i] = 0;
        }
        return false;
    }

 

三、Matchsticks to Square

问题描述：

问题求解：

k = 4.

    public boolean makesquare(int[] nums) {
        if (nums.length == 0) return false;
        int sum = 0;
        for (int num : nums) sum += num;
        if (sum % 4 != 0) return false;
        int eachSum = sum / 4;
        Arrays.sort(nums);
        return helper(nums, eachSum, 0, new int[nums.length], 0, 4);
    }

    private boolean helper(int[] nums, int eachSum, int curSum, int[] visited, int start, int k) {
        if (k == 0) return true;
        if (curSum > eachSum) return false;
        if (curSum == eachSum) return helper(nums, eachSum, 0, visited, 0, k - 1);
        for (int i = start; i < nums.length; i++) {
            if (visited[i] == 1 || (i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == 0)) continue;
            visited[i] = 1;
            if (helper(nums, eachSum, curSum + nums[i], visited, i + 1, k)) return true;
            visited[i] = 0;
        }
        return false;
    }

 

转载于:https://www.cnblogs.com/hyserendipity/p/9469891.html