抠图算法：经典的贝叶斯抠图

引言

数学无疑是现代数字图像处理技术和机器学习算法的一个共同的重要基石；此外，数字图像处理技术也从机器学习领域中汲取了许多智慧。例如，在face detection中，AdaBoost就有非常成功的应用。总之，当前一些效果显著的同时也非常popular的图像处理技术中大量地借鉴和利用了经典数学和机器学习理论中的一些著名的成果。数字图像抠图技术就是一个典型的领域，数学理论和机器学习方法在其中扮演了至关重要的角色。类似Naive Bayes和kkNN这样的机器学习方法在Image matting这个领域已经取得了非常好的效果。

图像抠图技术（Image Matting）在现代影视技术中有重要应用。这里所谓的“抠图”，英文Matting其实是“融合”的意思。所以如果翻译成图像融合技术其实也是恰当的的，但如果我们从“抠取”这个角度来看，Image Matting更类似于一种图像分割方法，只不过：1）它是一种超精细的图像分割技术；2）它要分割的内容通常是将前景从背景中分割（而广义的图像分割则还包括同等地位目标之间的分离）。

在图像抠图技术领域，人们已经开发了许多非常成功的算法，例如著名的贝叶斯抠图，kkNN抠图和泊松抠图（Poisson Matting）等等。本文将以图像抠图领域的经典算法——贝叶斯抠图（Bayesian Matting）为例来介绍有关图像抠图技术的一些内容。贝叶斯抠图源自文献【2】，是2001年发表在CVPR上的一篇经典论文。因为发表时间较早，所以自然也不可能是当前最先进或者应用最广泛的技术，但是作为一个教学目的之用的算法示例却是一个很好的选择。这个算法其实也不简单，但相对于其他抠图算法来说已经是技术细节比较浅显的一个典范了，而且后来的很多算法都或大或小地借鉴了其中的一些技术方法，所以在学习Image Matting是不应该错过这个算法的。文献【1】是罗切斯特理工学院Rich Radke教授主讲的计算机视觉课程中涉及到的Bayesian Matting部分，有兴趣的读者也可以通过此授课影片来学习该算法。

此处，我吐一个槽。Rich Radke教授的授课影片正是他在大学实际教授数字图像处理课程的录影。由此可见国外本科相关课程教学一是比较贴近实际、二是也紧跟学术发展，当然难度可能也有一定增加。反观国内的数字图像处理教学基本还在使用冈萨雷斯在40年前编写的《数字图像处理》教材（事实上，冈萨雷斯老师从高校退休也有快30多年了）。而像数字图像处理这种学科的发展速度是快到令人瞠目结舌的。因循守旧，墨守成规，我觉得这是我们应该好好注意并需要改进的地方。如果国外都在使用坚船利炮，我们还在大刀长矛，这样怎么能够在科技战争中取胜呢？

---

抠图算法的基本概念

图像抠图的核心问题就是求解下面这个Matting equation（在图像隐藏和图像去雾中都有类似的融合方程）：

C=αF−(1−α)BC=αF−(1−α)B

都是未知的，要把这么多未知项都求出来显然很不容易。所以就需要增加一些附加的约束，通常，这种约以TriMap的形式给出。TriMap就是三元图，它是和待分割图像同等大小的一张图，但图中的像素只有三个取值，0、128（左右）和255。例如上面的右图。其中黑色部分是确定知道的背景，白色是确定知道的前景。灰色是要做进一步精细划分的前景与背景交接地带，或者你可以解释为前景的边缘。

融合系数αα矩阵（矩阵元素的类型应该double，大小与trimp和原始图像一致）。

>> imshow(alpha)
   
   
   
   

   
   
   
   

    
    
    
    
1
   
   
   
   

然后再读入一张新的背景图片（如下图左所示），并将前景（经由 αα矩阵）融合到新的背景中，最终结果如下图右所示。

>> B = imread('background.png');
>> F = imread('input.png');
>> matting_result = makeComposite(F, B, alpha);
>> imshow(matting_result);
   
   
   
   

   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
   
   
   
   

上述代码中makeComposite函数的实现代码如下（由此我也不得不感叹MATLAB绝对是图像处理算法研究的最佳工具，借助其强大的矩阵运算能力，图像处理算法的代码在MATLAB中都非常精简）：

function C=makeComposite(F,B,alpha)

if ~isa(F,'double')
    F=im2double(F);
end
if ~isa(B,'double')
    B=im2double(B);
end

alpha=repmat(alpha,[1,1,size(F,3)]);
C=alpha.*F+(1-alpha).*B;
   
   
   
   

   
   
   
   

    
    
    
    
1
    
    
    
    
2
    
    
    
    
3
    
    
    
    
4
    
    
    
    
5
    
    
    
    
6
    
    
    
    
7
    
    
    
    
8
    
    
    
    
9
    
    
    
    
10
    
    
    
    
11
   
   
   
   

---

贝叶斯抠图算法

在融合方程中，已知的只有C，而F、B和αα的问题，即MAP问题。

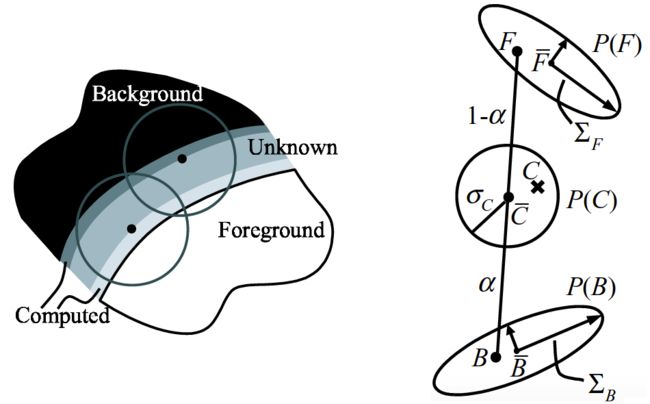
上述等式中的右端项，需要通过采样统计的方式进行估计，而这种估计结果的准确性，很大程度上决定了算法的融合质量。具体来说，算法采用一个连续滑动的窗口对邻域进行采样，窗口从未知区域和己知区域之间的两条边开始向内逐轮廓推进，计算过程也随之推进。下图左显示了Bayesian Matting方法的采样过程。

文献【2】中将采样窗口定义为一个以待计算点为中心，半径r的圆域。进行采样时，不但要对已知区域进行采样，同时为了在待计算像素周围保持一个连续的αα分布，也要对之前计算出的邻域像素点进行采样。需要说明的是，采样窗口必须覆盖己知的前景和背景区域。这是因为用户提供的Trimap不能保证一定是足够精致的，换句话说，未知区域覆盖的像素有很多是纯粹的前景或背景，而非混合像素。如果采样半径内不能保证有己知区域内的像素采样，就有可能造成无法采样到前景或背景色。

为了使重建出的颜色分布模型更具鲁棒性，在进行采样时，需要对窗口内的采样点的贡献度要进行加权。加权规则有两条，其一，根据αα（背景采样）。

算法的核心假设是在前景和背景的交界区域附近，其各自的颜色分布在局部应该是基本一致的。算法的目标是通过上面给出的采样统计结果，在未知区域的每一个待计算点上重建它的前景和背景颜色概率分布，并根据这种分布恢复出它的前景色F，背景色B和αα值。

跟朴素贝叶斯法中处理情况一致，因为P(C)是一个常数，所以在考虑最大化问题时可以将其忽略，再利用对数似然L(⋅)L(⋅)的过程。

算法将第一项建模为观察到像素CC也就越大。

算法在图像颜色空域一致性的假设前提下，对L(F)L(F)是一个常数值，并将其从原来的方程中舍去。当然这一点是值得讨论的。

L(C|F,B,α)L(C|F,B,α)项，所以它并不是关于未知数的二次方程。为了有效的求解这个等式，Bayesian matting算法将求解问题分为两个子问题来进行计算。

在第一步，假设αα的线性方程组得到最佳的估计色F和B。

第二步，假设F和B是常数，从而得到关于αα求导，并令其值为0，于是得到：

上述等式等价于将待计算像素的颜色C投影到线段FB上的投影值。如前面第4幅图中的右图所示，F, B分别表示估算出的前景色和背景色。

优化估计通过反复迭代上述第一步和第二步完成，首先用待计算像素周围的αα值的变化足够小或者迭代次数高于某一个阈值的时候停止。（这个思想其实跟EM算法有非常相像的地方。）

当有多个前景聚类和背景聚类的时候，算法对每一对前、背景聚类分别执行如上所述的优化求解,最后通过比较后验概率值的大小决定釆用哪一对的估算结果作为最终的计算结果。

现在用MATLAB来编程实现贝叶斯抠图算法，下面的代码将得到之前展示过的αα矩阵图像。

C=imread('input.png');
trimap=imread('trimap.png');

[F,B,alpha]=bayes_matting(C, trimap);
figure('Name','Alpha Result','NumberTitle','off');
imshow(alpha);
   
   
   
   

   
   
   
   

下面给出用来进行Bayesian Matting的核心函数代码，该代码原作者为Michael Rubinstein，笔者略有修改。

function [F,B,alpha]=bayes_matting(im,trimap)

%Necessary parameters setting, some parameters assignment are omitted here considering conciseness
% N, sigma, sigma_C, minN, clust.minVar, opt.maxIter, opt.minLike

im=im2double(im);
trimap=im2double(trimap);

bgmask=trimap==0; % background region mask
fgmask=trimap==1; % foreground region mask
unkmask=~bgmask&~fgmask; % unknow region mask

% initialize F,B,alpha
F=im; F(repmat(~fgmask,[1,1,3]))=0;
B=im; B(repmat(~bgmask,[1,1,3]))=0;
alpha=zeros(size(trimap));
alpha(fgmask)=1;
alpha(unkmask)=NaN;

nUnknown=sum(unkmask(:));

% guassian falloff. will be used for weighting each pixel neighborhood
g=fspecial('gaussian', N, sigma); g=g/max(g(:));
% square structuring element for eroding the unknown region(s)
se=strel('square',3);

n=1;
unkreg=unkmask;
while n% get unknown pixels to process at this iteration
    unkreg=imerode(unkreg,se);
    unkpixels=~unkreg&unkmask;
    [Y,X]=find(unkpixels); 

    for i=1:length(Y)

        % take current pixel
        x=X(i); y=Y(i);
        c = reshape(im(y,x,:),[3,1]);

        % take surrounding alpha values
        a=getN(alpha,x,y,N);

        % take surrounding foreground pixels
        f_pixels=getN(F,x,y,N);
        f_weights=(a.^2).*g;
        f_pixels=reshape(f_pixels, N*N, 3);
        f_pixels=f_pixels(f_weights>0,:);
        f_weights=f_weights(f_weights>0);

        % take surrounding background pixels
        b_pixels=getN(B,x,y,N);
        b_weights=((1-a).^2).*g;
        b_pixels=reshape(b_pixels, N*N, 3);
        b_pixels=b_pixels(b_weights>0,:);
        b_weights=b_weights(b_weights>0);

        % if not enough data, return to it later...
        if length(f_weights)length(b_weights)continue;
        end

        % partition foreground and background pixels to clusters (in a
        % weighted manner)
        [mu_f,Sigma_f]=cluster_OrachardBouman(f_pixels, f_weights, clust.minVar);
        [mu_b,Sigma_b]=cluster_OrachardBouman(b_pixels, b_weights, clust.minVar);

        % update covariances with camera variance, as mentioned in their
        % addendum
        Sigma_f=addCamVar(Sigma_f, sigma_C);
        Sigma_b=addCamVar(Sigma_b, sigma_C);

        % set initial alpha value to mean of surrounding pixels
        alpha_init=nanmean(a(:));

        % solve for current pixel
        [f,b,a]=solve(mu_f,Sigma_f,mu_b,Sigma_b,c,sigma_C,alpha_init,opt.maxIter,opt.minLike);

        F(y,x,:)=f;
        B(y,x,:)=b;
        alpha(y,x)=a;
        unkmask(y,x)=0; % remove from unkowns
        n=n+1;
    end
end

function r=getN(m,x,y,N)

[h,w,c]=size(m);
halfN = floor(N/2);
n1=halfN; n2=N-halfN-1;
r=nan(N,N,c);
xmin=max(1,x-n1);
xmax=min(w,x+n2);
ymin=max(1,y-n1);
ymax=min(h,y+n2);
pxmin=halfN-(x-xmin)+1; pxmax=halfN+(xmax-x)+1;
pymin=halfN-(y-ymin)+1; pymax=halfN+(ymax-y)+1;
r(pymin:pymax,pxmin:pxmax,:)=m(ymin:ymax,xmin:xmax,:);

% finds the orientation of the covariance matrices, and adds the camera
% variance to each axis
function Sigma=addCamVar(Sigma,sigma_C)

Sigma=zeros(size(Sigma));
for i=1:size(Sigma,3)
    Sigma_i=Sigma(:,:,i);
    [U,S,V]=svd(Sigma_i);
    Sp=S+diag([sigma_C^2,sigma_C^2,sigma_C^2]);
    Sigma(:,:,i)=U*Sp*V';
end
   
   
   
   

   
   
   
   

更多图像处理中的数学问题请参考《图像处理中的数学修炼》，也欢迎广大读者到图像处理书籍读者群中参与讨论学习，并交流关于Bayesian Matting、Poisson Matting等抠图算法的研究心得。

VIEWER DISCRETION IS ADVISED!!! 如果你觉得本篇博客文章中哪里描述欠妥，请参考算法作者原文，一切以作者的原文为准，笔者不对由于个人理解差异所导致的博文中之纰漏负责。

---

参考文献

【1】 罗切斯特理工学院Rich Radke教授主讲的计算机视觉公开课-Lec2: Bayesian Matting（注意自备梯子，网页最后浏览时间 2017.06）
【2】 Yung-Yu Chuang, B. Curless, D.H. Salesin, and R. Szeliski, A Bayesian Approach to Digital Matting. CVPR, 2001. （项目主页及论文下载，网页最后浏览时间 2017.06）
【3】 关于另外一种抠图算法（Shared Sampling for Real-Time Alpha Matting）的解读，请参考链接（网页最后浏览时间 2017.06）
【4】 一篇关于Bayesian Matting算法研究的硕士毕业论文（网页最后浏览时间 2017.06）
【5】 M. T. Orchard and C. A. Bouman. Color Quantization of Images. IEEE Transactions on Signal Processing, 39(12):2677–2690, December 1991.（下载链接，网页最后浏览时间 2017.06）